Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 163171 by ZiYangLee last updated on 04/Jan/22

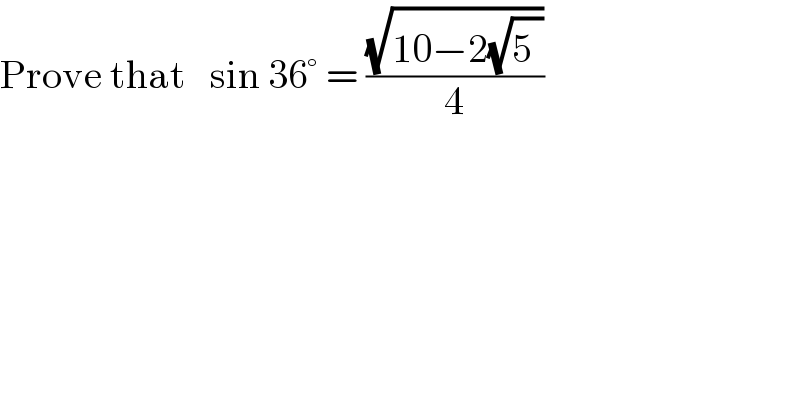
Prove that sin 36° = ((√(10−2(√5^ )))/4)

$$\mathrm{Prove}\:\mathrm{that}\:\:\:\mathrm{sin}\:\mathrm{36}°\:=\:\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}^{} }}}{\mathrm{4}} \\ $$

Answered by mr W last updated on 04/Jan/22

sin (3×18^° )=sin (54°)=cos (36°)=cos (2×18°) 3 sin 18°−4 sin^3 18°=1−2 sin^2 18° let t=sin 18° 3t−4t^3 =1−2t^2 4t^3 −2t^2 −3t+1=0 4t^3 −4t^2 +2t^2 −2t−t+1=0 (t−1)(4t^2 +2t−1)=0 t≠1 ⇒4t^2 +2t−1=0 ⇒t=((−1+(√5))/4)=sin 18° cos 18°=(√(1−((((√5)−1)/4))^2 ))=((√(10+2(√5)))/4) sin 36°=2 sin 18° cos 18° =2×((−1+(√5))/4)×((√(10+2(√5)))/4) =((√((10+2(√5))(6−2(√5))))/8) =((√(10−2(√5)))/4)

$$\mathrm{sin}\:\left(\mathrm{3}×\mathrm{18}^{°} \right)=\mathrm{sin}\:\left(\mathrm{54}°\right)=\mathrm{cos}\:\left(\mathrm{36}°\right)=\mathrm{cos}\:\left(\mathrm{2}×\mathrm{18}°\right) \\ $$$$\mathrm{3}\:\mathrm{sin}\:\mathrm{18}°−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\mathrm{18}°=\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{18}° \\ $$$${let}\:{t}=\mathrm{sin}\:\mathrm{18}° \\ $$$$\mathrm{3}{t}−\mathrm{4}{t}^{\mathrm{3}} =\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \\ $$$$\mathrm{4}{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}−{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$${t}\neq\mathrm{1} \\ $$$$\Rightarrow\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}=\mathrm{sin}\:\mathrm{18}° \\ $$$$\mathrm{cos}\:\mathrm{18}°=\sqrt{\mathrm{1}−\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{36}°=\mathrm{2}\:\mathrm{sin}\:\mathrm{18}°\:\mathrm{cos}\:\mathrm{18}° \\ $$$$\:\:\:\:\:\:=\mathrm{2}×\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}×\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:=\frac{\sqrt{\left(\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}\right)\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\right)}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:=\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$

Commented by peter frank last updated on 05/Jan/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Commented by henderson last updated on 07/Jan/22

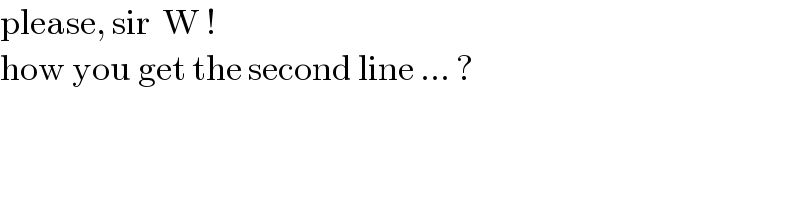
please, sir W ! how you get the second line ... ?

$$\mathrm{please},\:\mathrm{sir}\:\:\mathrm{W}\:! \\ $$$$\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{second}\:\mathrm{line}\:...\:?\: \\ $$

Commented by mr W last updated on 07/Jan/22

the formulas for sin 3α and cos 3α are very useful. you should memorise them. but if you can′t, you can also get them easily like in following way: sin 3α =sin (2α+α) =sin 2α cos α+cos 2α sin α =2sin α cos^2 α+(1−2 sin^2 α) sin α =2sin α (1−sin^2 α)+(1−2 sin^2 α) sin α =2sin α −2 sin^3 α+ sin α−2 sin^3 α =3sin α −4 sin^3 α =(3−4 sin^2 α)sin α

$${the}\:{formulas}\:{for}\:\mathrm{sin}\:\mathrm{3}\alpha\:{and}\:\mathrm{cos}\:\mathrm{3}\alpha \\ $$$${are}\:{very}\:{useful}.\:{you}\:{should}\:{memorise} \\ $$$${them}.\:{but}\:{if}\:{you}\:{can}'{t},\:{you}\:{can}\:{also} \\ $$$${get}\:{them}\:{easily}\:{like}\:{in}\:{following}\:{way}: \\ $$$$\mathrm{sin}\:\mathrm{3}\alpha \\ $$$$=\mathrm{sin}\:\left(\mathrm{2}\alpha+\alpha\right) \\ $$$$=\mathrm{sin}\:\mathrm{2}\alpha\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\mathrm{2}\alpha\:\mathrm{sin}\:\alpha \\ $$$$=\mathrm{2sin}\:\alpha\:\mathrm{cos}^{\mathrm{2}} \:\alpha+\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha\right)\:\mathrm{sin}\:\alpha \\ $$$$=\mathrm{2sin}\:\alpha\:\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\alpha\right)+\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha\right)\:\mathrm{sin}\:\alpha \\ $$$$=\mathrm{2sin}\:\alpha\:−\mathrm{2}\:\mathrm{sin}^{\mathrm{3}} \:\alpha+\:\mathrm{sin}\:\alpha−\mathrm{2}\:\mathrm{sin}^{\mathrm{3}} \:\alpha \\ $$$$=\mathrm{3sin}\:\alpha\:−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\alpha \\ $$$$=\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\alpha\right)\mathrm{sin}\:\alpha \\ $$

Commented by greg_ed last updated on 07/Jan/22

very good

$$\mathrm{very}\:\mathrm{good} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com