Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 163313 by SLVR last updated on 06/Jan/22

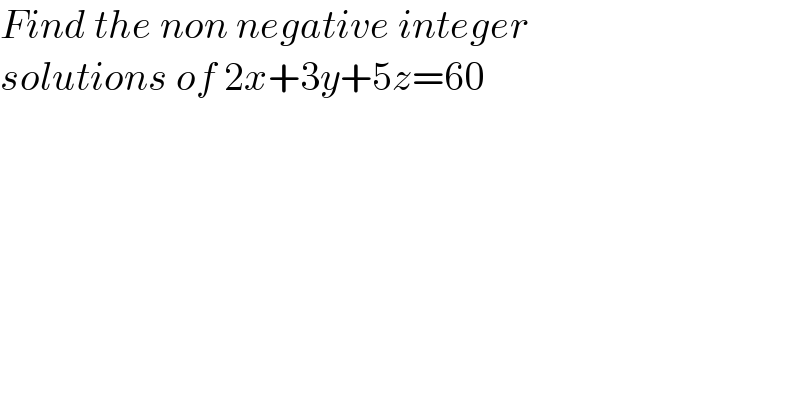
Find the non negative integer solutions of 2x+3y+5z=60

$${Find}\:{the}\:{non}\:{negative}\:{integer} \\ $$$${solutions}\:{of}\:\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{5}{z}=\mathrm{60} \\ $$

Answered by mr W last updated on 06/Jan/22

let 2x+3y=5u 5u+5z=60 u+z=12 ⇒u=n with n ∈ Z ⇒z=12−n 2x+3y=1 x=3k−1 with k ∈ Z y=−2k+1 2x+3y=5u=5n x=5n(3k−1)=3(5nk)−5n=3m−5n y=5n(−2k+1)=−2(5nk)+5n=−2m+5n general solution: { ((x=3m−5n)),((y=−2m+5n)),((z=12−n)) :} (with m,n∈Z) non−negative solutions: z=12−n≥0 ⇒n≤12 x=3m−5n≥0 y=−2m+5n≥0 ⇒0≤n≤12 ⇒((5n)/3)≤m≤((5n)/2) totally there are 71 solutions: n=0: m=0 n=1: m=2 n=2: m=3, 4 n=3: m=5, 6, 7 .... n=12: m=20, 21, ..., 30

$${let}\:\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{5}{u} \\ $$$$\mathrm{5}{u}+\mathrm{5}{z}=\mathrm{60} \\ $$$${u}+{z}=\mathrm{12} \\ $$$$\Rightarrow{u}={n}\:{with}\:{n}\:\in\:\mathbb{Z} \\ $$$$\Rightarrow{z}=\mathrm{12}−{n} \\ $$$$ \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{1} \\ $$$${x}=\mathrm{3}{k}−\mathrm{1}\:{with}\:{k}\:\in\:\mathbb{Z} \\ $$$${y}=−\mathrm{2}{k}+\mathrm{1} \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{5}{u}=\mathrm{5}{n} \\ $$$${x}=\mathrm{5}{n}\left(\mathrm{3}{k}−\mathrm{1}\right)=\mathrm{3}\left(\mathrm{5}{nk}\right)−\mathrm{5}{n}=\mathrm{3}{m}−\mathrm{5}{n} \\ $$$${y}=\mathrm{5}{n}\left(−\mathrm{2}{k}+\mathrm{1}\right)=−\mathrm{2}\left(\mathrm{5}{nk}\right)+\mathrm{5}{n}=−\mathrm{2}{m}+\mathrm{5}{n} \\ $$$$ \\ $$$${general}\:{solution}: \\ $$$$\begin{cases}{{x}=\mathrm{3}{m}−\mathrm{5}{n}}\\{{y}=−\mathrm{2}{m}+\mathrm{5}{n}}\\{{z}=\mathrm{12}−{n}}\end{cases}\:\:\:\:\:\left({with}\:{m},{n}\in\mathbb{Z}\right) \\ $$$${non}−{negative}\:{solutions}: \\ $$$${z}=\mathrm{12}−{n}\geqslant\mathrm{0}\:\Rightarrow{n}\leqslant\mathrm{12} \\ $$$${x}=\mathrm{3}{m}−\mathrm{5}{n}\geqslant\mathrm{0} \\ $$$${y}=−\mathrm{2}{m}+\mathrm{5}{n}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{0}\leqslant{n}\leqslant\mathrm{12} \\ $$$$\Rightarrow\frac{\mathrm{5}{n}}{\mathrm{3}}\leqslant{m}\leqslant\frac{\mathrm{5}{n}}{\mathrm{2}} \\ $$$${totally}\:{there}\:{are}\:\mathrm{71}\:{solutions}: \\ $$$${n}=\mathrm{0}:\:{m}=\mathrm{0} \\ $$$${n}=\mathrm{1}:\:{m}=\mathrm{2} \\ $$$${n}=\mathrm{2}:\:{m}=\mathrm{3},\:\mathrm{4} \\ $$$${n}=\mathrm{3}:\:{m}=\mathrm{5},\:\mathrm{6},\:\mathrm{7} \\ $$$$.... \\ $$$${n}=\mathrm{12}:\:{m}=\mathrm{20},\:\mathrm{21},\:...,\:\mathrm{30} \\ $$

Commented by SLVR last updated on 06/Jan/22

Wow...really great enough..we are blessed...with your service

$${Wow}...{really}\:{great}\:{enough}..{we} \\ $$$${are}\:{blessed}...{with}\:{your}\:{service} \\ $$

Commented by mr W last updated on 06/Jan/22

Commented by mr W last updated on 06/Jan/22

note: number of non negative solutions of 2x+3y+5z=60 is the coef. of term x^(60) in the expansion of (1+x^2 +x^4 +...)(1+x^3 +x^6 +...)(1+x^5 +x^(10) +...) =(1/((1−x^2 )(1−x^3 )(1−x^5 ))). that is 71.

$$\underline{{note}:} \\ $$$${number}\:{of}\:{non}\:{negative}\:{solutions}\:{of} \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{5}{z}=\mathrm{60}\:{is}\:{the}\:{coef}.\:{of}\:{term}\:{x}^{\mathrm{60}} \\ $$$${in}\:{the}\:{expansion}\:{of}\: \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +...\right)\left(\mathrm{1}+{x}^{\mathrm{3}} +{x}^{\mathrm{6}} +...\right)\left(\mathrm{1}+{x}^{\mathrm{5}} +{x}^{\mathrm{10}} +...\right) \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{3}} \right)\left(\mathrm{1}−{x}^{\mathrm{5}} \right)}.\:{that}\:{is}\:\mathrm{71}. \\ $$

Commented by mr W last updated on 06/Jan/22

Commented by Rasheed.Sindhi last updated on 06/Jan/22

M RE _(THAN_(P∈RF∈⊂T !) ) Multimedia(graph) & number of solutions are in addition! ThanX sir!

$$\underset{\underset{\mathcal{P}\in\mathcal{RF}\in\subset\mathcal{T}\:\:!} {\mathrm{THAN}}} {\mathcal{M} \mathcal{RE}\:} \\ $$$$\mathbb{M}\mathrm{ultimedia}\left(\mathrm{graph}\right) \\ $$$$\&\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\: \\ $$$$\:\mathrm{are}\:\:\mathrm{in}\:\mathrm{addition}! \\ $$$$\mathcal{T}{han}\mathcal{X}\:\boldsymbol{{sir}}! \\ $$

Commented by mr W last updated on 06/Jan/22

thanks sirs! graph helps very much to find out if errors are made. therefore i like to work with graph.

$${thanks}\:{sirs}! \\ $$$${graph}\:{helps}\:{very}\:{much}\:{to}\:{find}\:{out}\:{if}\: \\ $$$${errors}\:{are}\:{made}.\:{therefore}\:{i}\:{like}\:{to}\: \\ $$$${work}\:{with}\:{graph}. \\ $$

Commented by Tawa11 last updated on 06/Jan/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by Rasheed.Sindhi last updated on 07/Jan/22

SHARING: https://youtu.be/fw1kRz83Fj0

Commented by SLVR last updated on 31/Jan/22

Respected prof.W...evaluation of x^(60) with out original mul tlication all terms complnent wise..kindly with general term of expansion.please

$${Respected}\:{prof}.{W}...{evaluation} \\ $$$${of}\:{x}^{\mathrm{60}} \:{with}\:{out}\:{original}\:{mul} \\ $$$${tlication}\:{all}\:{terms}\:{complnent} \\ $$$${wise}..{kindly}\:\:{with}\:{general} \\ $$$${term}\:{of}\:{expansion}.{please} \\ $$

Commented by mr W last updated on 31/Jan/22

please express clearly what you want to have!

$${please}\:{express}\:{clearly}\:{what}\:{you}\:{want} \\ $$$${to}\:{have}! \\ $$

Commented by SLVR last updated on 02/Feb/22

Sir...I mean to say .. coeffitient of x^(60) in (1−x^2 )(1−x^3 )(1−x^5 ) not by multiplying all terms but possibility of general term of(1−x)^(−1) C_r ^(n+r−1) ... Or getting the coeffitient of x^(60) as 71 in a easy way??? Please..sir...

$${Sir}...{I}\:{mean}\:{to}\:{say}\:.. \\ $$$${coeffitient}\:{of}\:{x}^{\mathrm{60}} \:{in}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{3}} \right)\left(\mathrm{1}−{x}^{\mathrm{5}} \right) \\ $$$${not}\:{by}\:{multiplying}\:{all}\:{terms} \\ $$$${but}\:{possibility}\:{of}\:{general}\:{term}\:{of}\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} \\ $$$${C}_{{r}} ^{{n}+{r}−\mathrm{1}} \:...\:{Or}\:{getting}\:{the}\:{coeffitient} \\ $$$${of}\:{x}^{\mathrm{60}} \:\:{as}\:\mathrm{71}\:{in}\:{a}\:{easy}\:{way}??? \\ $$$${Please}..{sir}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 02/Feb/22

in fact there is no easy way to determine the coefficient of a general term.

$${in}\:{fact}\:{there}\:{is}\:{no}\:{easy}\:{way}\:{to}\: \\ $$$${determine}\:{the}\:{coefficient}\:{of}\:{a}\: \\ $$$${general}\:{term}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com