
Question and Answers Forum
Question Number 163402 by Ahmed777hamouda last updated on 06/Jan/22
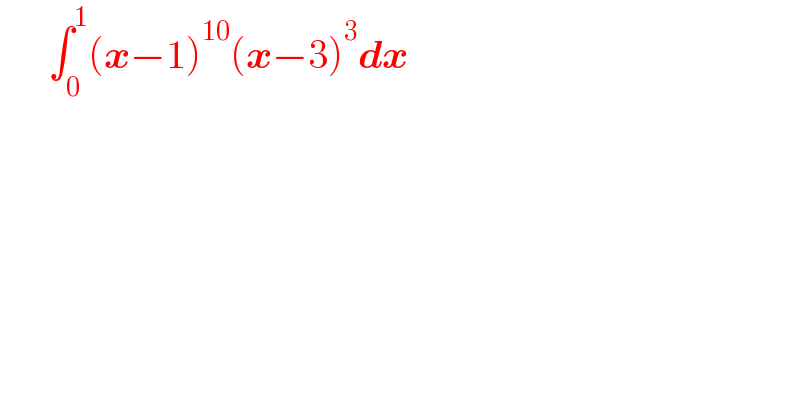
Answered by Ar Brandon last updated on 06/Jan/22
![I=∫_0 ^1 (x−1)^(10) (x−3)^3 dx, t=x−3 =∫_(−3) ^(−2) (t+2)^(10) t^3 dt=[((t^3 (t+2)^(11) )/(11))]_(−3) ^(−2) −(3/(11))∫_(−3) ^(−2) t^2 (t+2)^(11) dt =−((27)/(11))−(3/(11))[((t^2 (t+2)^(12) )/(12))]_(−3) ^(−2) +(3/(11))∙(2/(12))∫_(−3) ^(−2) t(t+2)^(12) dt =−((27)/(11))+((27)/(11×12))+(1/(22))[((t(t+2)^(13) )/(13))]_(−3) ^(−2) −(1/(22))∙(1/(13))∫_(−3) ^(−2) (t+2)^(13) dt =−((27)/(11))+((27)/(132))−(1/(22))∙(3/(13))−(1/(22×13))∙[(((t+2)^(14) )/(14))]_(−3) ^(−2) =−((27)/(11))+((27)/(132))−(3/(286))−(1/(286×14))=−((4525)/(2002))](Q163406.png)
Commented by peter frank last updated on 07/Jan/22

| ||
Question and Answers Forum | ||
Question Number 163402 by Ahmed777hamouda last updated on 06/Jan/22 | ||
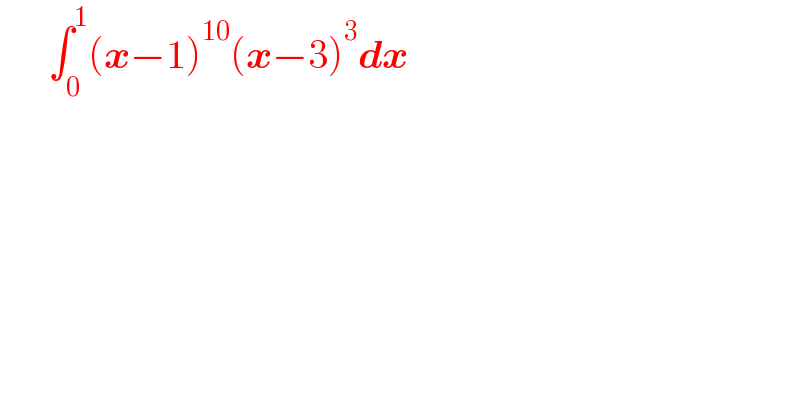 | ||
Answered by Ar Brandon last updated on 06/Jan/22 | ||
![I=∫_0 ^1 (x−1)^(10) (x−3)^3 dx, t=x−3 =∫_(−3) ^(−2) (t+2)^(10) t^3 dt=[((t^3 (t+2)^(11) )/(11))]_(−3) ^(−2) −(3/(11))∫_(−3) ^(−2) t^2 (t+2)^(11) dt =−((27)/(11))−(3/(11))[((t^2 (t+2)^(12) )/(12))]_(−3) ^(−2) +(3/(11))∙(2/(12))∫_(−3) ^(−2) t(t+2)^(12) dt =−((27)/(11))+((27)/(11×12))+(1/(22))[((t(t+2)^(13) )/(13))]_(−3) ^(−2) −(1/(22))∙(1/(13))∫_(−3) ^(−2) (t+2)^(13) dt =−((27)/(11))+((27)/(132))−(1/(22))∙(3/(13))−(1/(22×13))∙[(((t+2)^(14) )/(14))]_(−3) ^(−2) =−((27)/(11))+((27)/(132))−(3/(286))−(1/(286×14))=−((4525)/(2002))](Q163406.png) | ||
| ||
Commented by peter frank last updated on 07/Jan/22 | ||
 | ||