Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 163483 by Zaynal last updated on 07/Jan/22

	Answered by alephzero last updated on 07/Jan/22
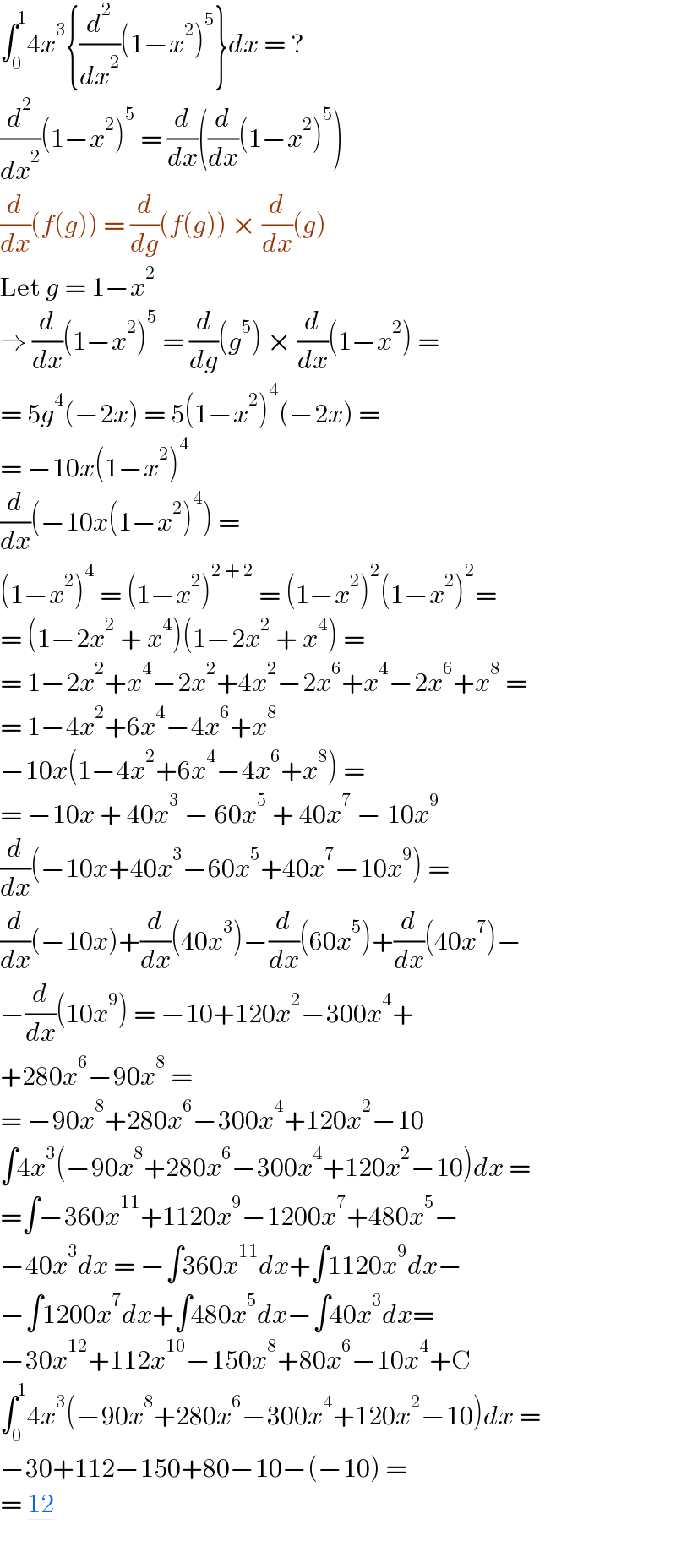
	$∫_0 ^1 4x^3 {(d^2 /dx^2 )(1−x^2 )^5 }dx = ? (d^2 /dx^2 )(1−x^2 )^5 = (d/dx)((d/dx)(1−x^2 )^5 ) (d/dx)(f(g)) = (d/dg)(f(g)) × (d/dx)(g) Let g = 1−x^2 ⇒ (d/dx)(1−x^2 )^5 = (d/dg)(g^5 ) × (d/dx)(1−x^2 ) = = 5g^4 (−2x) = 5(1−x^2 )^4 (−2x) = = −10x(1−x^2 )^4 (d/dx)(−10x(1−x^2 )^4 ) = (1−x^2 )^4 = (1−x^2 )^(2 + 2) = (1−x^2 )^2 (1−x^2 )^2 = = (1−2x^2 + x^4 )(1−2x^2 + x^4 ) = = 1−2x^2 +x^4 −2x^2 +4x^2 −2x^6 +x^4 −2x^6 +x^8 = = 1−4x^2 +6x^4 −4x^6 +x^8 −10x(1−4x^2 +6x^4 −4x^6 +x^8 ) = = −10x + 40x^3 − 60x^5 + 40x^7 − 10x^9 (d/dx)(−10x+40x^3 −60x^5 +40x^7 −10x^9 ) = (d/dx)(−10x)+(d/dx)(40x^3 )−(d/dx)(60x^5 )+(d/dx)(40x^7 )− −(d/dx)(10x^9 ) = −10+120x^2 −300x^4 + +280x^6 −90x^8 = = −90x^8 +280x^6 −300x^4 +120x^2 −10 ∫4x^3 (−90x^8 +280x^6 −300x^4 +120x^2 −10)dx = =∫−360x^(11) +1120x^9 −1200x^7 +480x^5 − −40x^3 dx = −∫360x^(11) dx+∫1120x^9 dx− −∫1200x^7 dx+∫480x^5 dx−∫40x^3 dx= −30x^(12) +112x^(10) −150x^8 +80x^6 −10x^4 +C ∫_0 ^1 4x^3 (−90x^8 +280x^6 −300x^4 +120x^2 −10)dx = −30+112−150+80−10−(−10) = = 12$
	$\int_{0}^{1} 4 x^{3} {\frac{d^{2}}{{d x}^{2}} {(1 - x^{2})}^{5}} d x = ?$ $\frac{d^{2}}{{d x}^{2}} {(1 - x^{2})}^{5} = \frac{d}{d x} (\frac{d}{d x} {(1 - x^{2})}^{5})$ $\underset{―}{\frac{d}{d x} (f (g)) = \frac{d}{d g} (f (g)) \times \frac{d}{d x} (g)}$ $Let g = 1 - x^{2}$ $\Rightarrow \frac{d}{d x} {(1 - x^{2})}^{5} = \frac{d}{d g} (g^{5}) \times \frac{d}{d x} (1 - x^{2}) =$ $= 5 g^{4} (- 2 x) = 5 {(1 - x^{2})}^{4} (- 2 x) =$ $= - 10 x {(1 - x^{2})}^{4}$ $\frac{d}{d x} (- 10 x {(1 - x^{2})}^{4}) =$ ${(1 - x^{2})}^{4} = {(1 - x^{2})}^{2 + 2} = {(1 - x^{2})}^{2} {(1 - x^{2})}^{2} =$ $= (1 - 2 x^{2} + x^{4}) (1 - 2 x^{2} + x^{4}) =$ $= 1 - 2 x^{2} + x^{4} - 2 x^{2} + 4 x^{2} - 2 x^{6} + x^{4} - 2 x^{6} + x^{8} =$ $= 1 - 4 x^{2} + 6 x^{4} - 4 x^{6} + x^{8}$ $- 10 x (1 - 4 x^{2} + 6 x^{4} - 4 x^{6} + x^{8}) =$ $= - 10 x + 40 x^{3} - 60 x^{5} + 40 x^{7} - 10 x^{9}$ $\frac{d}{d x} (- 10 x + 40 x^{3} - 60 x^{5} + 40 x^{7} - 10 x^{9}) =$ $\frac{d}{d x} (- 10 x) + \frac{d}{d x} (40 x^{3}) - \frac{d}{d x} (60 x^{5}) + \frac{d}{d x} (40 x^{7}) -$ $- \frac{d}{d x} (10 x^{9}) = - 10 + 120 x^{2} - 300 x^{4} +$ $+ 280 x^{6} - 90 x^{8} =$ $= - 90 x^{8} + 280 x^{6} - 300 x^{4} + 120 x^{2} - 10$ $\int 4 x^{3} (- 90 x^{8} + 280 x^{6} - 300 x^{4} + 120 x^{2} - 10) d x =$ $= \int - 360 x^{11} + 1120 x^{9} - 1200 x^{7} + 480 x^{5} -$ $- 40 x^{3} d x = - \int 360 x^{11} d x + \int 1120 x^{9} d x -$ $- \int 1200 x^{7} d x + \int 480 x^{5} d x - \int 40 x^{3} d x =$ $- 30 x^{12} + 112 x^{10} - 150 x^{8} + 80 x^{6} - 10 x^{4} + C$ $\int_{0}^{1} 4 x^{3} (- 90 x^{8} + 280 x^{6} - 300 x^{4} + 120 x^{2} - 10) d x =$ $- 30 + 112 - 150 + 80 - 10 - (- 10) =$ $= \underset{―}{12}$
	Commented by Zaynal last updated on 07/Jan/22

	$ans is 2$
	Answered by mr W last updated on 07/Jan/22
	$(d/dx)(1−x^2 )^5 =5(1−x^2 )^4 (−2x) (d^2 /dx^2 )(1−x^2 )^5 =−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 ∫_0 ^1 4x^3 {−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 }dx =∫_0 ^1 2x^2 {−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 }d(x^2 ) =20∫_0 ^1 u(9u−1)(1−u)^3 du =20∫_0 ^1 (u−1+1)(−9(u−1)−8)(u−1)^3 d(u−1) =20∫_(−1) ^0 (t+1)(−9t−8)t^3 dt =20∫_0 ^(−1) (t+1)(9t+8)t^3 dt =20∫_0 ^(−1) (9t^5 +17t^4 +8t^3 )dt =20[((3t^6 )/2)+((17t^5 )/5)+2t^4 ]_0 ^(−1) dt =20((3/2)−((17)/5)+2) =20×(1/(10)) =2$
	$\frac{d}{d x} {(1 - x^{2})}^{5} = 5 {(1 - x^{2})}^{4} (- 2 x)$ $\frac{d^{2}}{{d x}^{2}} {(1 - x^{2})}^{5} = - 10 {(1 - x^{2})}^{4} + 80 x^{2} {(1 - x^{2})}^{3}$ $\int_{0}^{1} 4 x^{3} {- 10 {(1 - x^{2})}^{4} + 80 x^{2} {(1 - x^{2})}^{3}} d x$ $= \int_{0}^{1} 2 x^{2} {- 10 {(1 - x^{2})}^{4} + 80 x^{2} {(1 - x^{2})}^{3}} d (x^{2})$ $= 20 \int_{0}^{1} u (9 u - 1) {(1 - u)}^{3} d u$ $= 20 \int_{0}^{1} (u - 1 + 1) (- 9 (u - 1) - 8) {(u - 1)}^{3} d (u - 1)$ $= 20 \int_{- 1}^{0} (t + 1) (- 9 t - 8) t^{3} d t$ $= 20 \int_{0}^{- 1} (t + 1) (9 t + 8) t^{3} d t$ $= 20 \int_{0}^{- 1} (9 t^{5} + 17 t^{4} + 8 t^{3}) d t$ $= 20 {[\frac{3 t^{6}}{2} + \frac{17 t^{5}}{5} + 2 t^{4}]}_{0}^{- 1} d t$ $= 20 (\frac{3}{2} - \frac{17}{5} + 2)$ $= 20 \times \frac{1}{10}$ $= 2$
	Answered by Ar Brandon last updated on 07/Jan/22
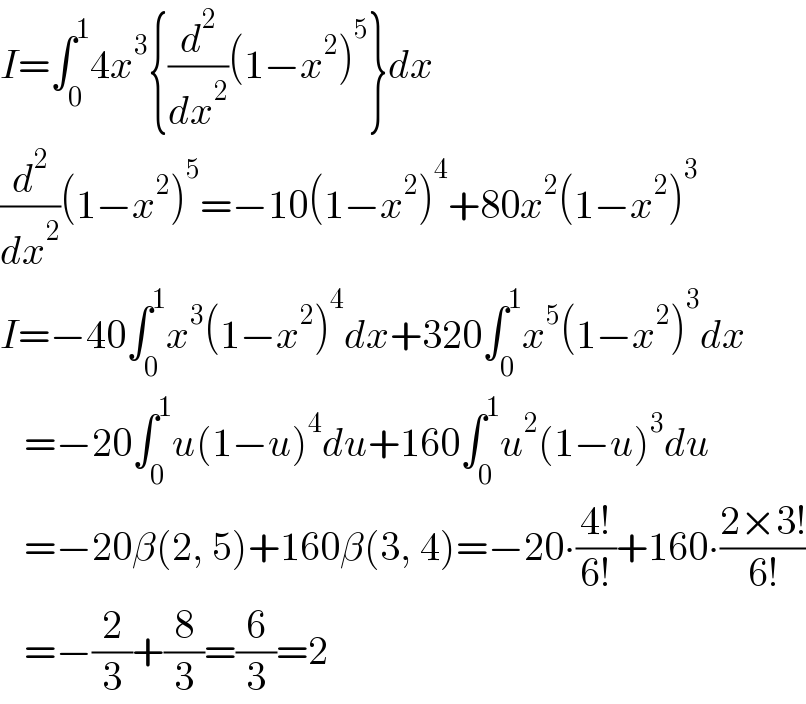
	$I=∫_0 ^1 4x^3 {(d^2 /dx^2 )(1−x^2 )^5 }dx (d^2 /dx^2 )(1−x^2 )^5 =−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 I=−40∫_0 ^1 x^3 (1−x^2 )^4 dx+320∫_0 ^1 x^5 (1−x^2 )^3 dx =−20∫_0 ^1 u(1−u)^4 du+160∫_0 ^1 u^2 (1−u)^3 du =−20β(2, 5)+160β(3, 4)=−20∙((4!)/(6!))+160∙((2×3!)/(6!)) =−(2/3)+(8/3)=(6/3)=2$
	$I = \int_{0}^{1} 4 x^{3} {\frac{d^{2}}{{d x}^{2}} {(1 - x^{2})}^{5}} d x$ $\frac{d^{2}}{{d x}^{2}} {(1 - x^{2})}^{5} = - 10 {(1 - x^{2})}^{4} + 80 x^{2} {(1 - x^{2})}^{3}$ $I = - 40 \int_{0}^{1} x^{3} {(1 - x^{2})}^{4} d x + 320 \int_{0}^{1} x^{5} {(1 - x^{2})}^{3} d x$ $= - 20 \int_{0}^{1} u {(1 - u)}^{4} d u + 160 \int_{0}^{1} u^{2} {(1 - u)}^{3} d u$ $= - 20 β (2, 5) + 160 β (3, 4) = - 20 \cdot \frac{4!}{6!} + 160 \cdot \frac{2 \times 3!}{6!}$ $= - \frac{2}{3} + \frac{8}{3} = \frac{6}{3} = 2$
	Answered by ajfour last updated on 07/Jan/22
	$x^2 =t ∫_0 ^( 1) 2t{(d^2 /dx^2 )(1−x^2 )^5 }dt =∫(d/dx){5(−2x)(1−x^2 )^4 }2tdt =5∫_0 ^( 1) {16t(1−t)^3 −2(1−t)^4 }(2tdt) =10∫_0 ^( 1) {16(1−t)t^3 −2t^4 }(1−t)dt =10∫{16t^3 −18t^4 )(1−t)dt =10∫_0 ^( 1) (16t^3 −16t^4 −18t^4 +18t^5 )dt =10[4−((34)/5)+3]=70−68 = 2 (got it).$
	$x^{2} = t$ $\int_{0}^{1} 2 t {\frac{d^{2}}{{d x}^{2}} {(1 - x^{2})}^{5}} d t$ $= \int \frac{d}{d x} {5 (- 2 x) {(1 - x^{2})}^{4}} 2 t d t$ $= 5 \int_{0}^{1} {16 t {(1 - t)}^{3} - 2 {(1 - t)}^{4}} (2 t d t)$ $= 10 \int_{0}^{1} {16 (1 - t) t^{3} - 2 t^{4}} (1 - t) d t$ $= 10 \int {16 t^{3} - 18 t^{4}) (1 - t) d t$ $= 10 \int_{0}^{1} (16 t^{3} - 16 t^{4} - 18 t^{4} + 18 t^{5}) d t$ $= 10 [4 - \frac{34}{5} + 3] = 70 - 68 = 2 (g o t i t) .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum