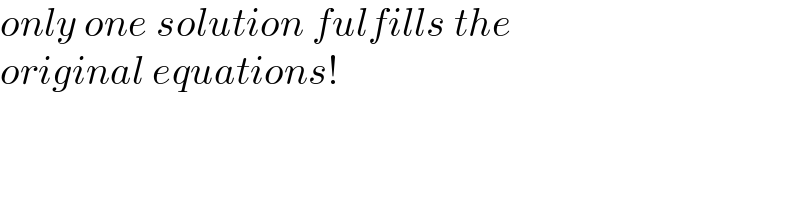Math Question and Answers


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 163627 by nurtani last updated on 08/Jan/22

	Answered by mr W last updated on 08/Jan/22
	$u=(1/(x+y)) >0 v=xy (√(21v))(1−u^2 )=8(√2) v=((128)/(21(1−u^2 )^2 )) x=(4/(3(1+u)^2 )) y=((32)/(7(1−u)^2 )) u=(1/(x+y))=(1/((4/(3(1+u)^2 ))+((32)/(7(1−u)^2 ))))=((21(1−u^2 )^2 )/(4[7(1−u)^2 +24(1+u)^2 ])) 4u=((21−42u^2 +21u^4 )/(31u^2 +34u+31)) 21u^4 −124u^3 −178u^2 −124u+21=0 (3u^2 −22u+3)(7u^2 +10u+7)=0 3u^2 −22u+3=0 u=((11−4(√7))/3) x+y=(1/u)=((11+4(√7))/3) xy=v=((128)/(21(1−u^2 )^2 ))=((466+176(√7))/(147)) x,y are roots of z^2 −((11+4(√7))/3)z+((466+176(√7))/(147))=0 x,y=(1/2){((11+4(√7))/3)±(√((((11+4(√7))/3))^2 −4(((466+176(√7))/(147)))))} x=(1/6){11+4(√7)−((5(√(233+88(√7))))/7)}≈1.0278 y=(1/6){11+4(√7)+((5(√(233+88(√7))))/7)}≈6.1666$
	$u = \frac{1}{x + y} > 0$ $v = x y$ $\sqrt{21 v} (1 - u^{2}) = 8 \sqrt{2}$ $v = \frac{128}{21 {(1 - u^{2})}^{2}}$ $x = \frac{4}{3 {(1 + u)}^{2}}$ $y = \frac{32}{7 {(1 - u)}^{2}}$ $u = \frac{1}{x + y} = \frac{1}{\frac{4}{3 {(1 + u)}^{2}} + \frac{32}{7 {(1 - u)}^{2}}} = \frac{21 {(1 - u^{2})}^{2}}{4 [7 {(1 - u)}^{2} + 24 {(1 + u)}^{2}]}$ $4 u = \frac{21 - 42 u^{2} + 21 u^{4}}{31 u^{2} + 34 u + 31}$ $21 u^{4} - 124 u^{3} - 178 u^{2} - 124 u + 21 = 0$ $(3 u^{2} - 22 u + 3) (7 u^{2} + 10 u + 7) = 0$ $3 u^{2} - 22 u + 3 = 0$ $u = \frac{11 - 4 \sqrt{7}}{3}$ $x + y = \frac{1}{u} = \frac{11 + 4 \sqrt{7}}{3}$ $x y = v = \frac{128}{21 {(1 - u^{2})}^{2}} = \frac{466 + 176 \sqrt{7}}{147}$ $x, y a r e r o o t s o f$ $z^{2} - \frac{11 + 4 \sqrt{7}}{3} z + \frac{466 + 176 \sqrt{7}}{147} = 0$ $x, y = \frac{1}{2} {\frac{11 + 4 \sqrt{7}}{3} \pm \sqrt{{(\frac{11 + 4 \sqrt{7}}{3})}^{2} - 4 (\frac{466 + 176 \sqrt{7}}{147})}}$ $x = \frac{1}{6} {11 + 4 \sqrt{7} - \frac{5 \sqrt{233 + 88 \sqrt{7}}}{7}} \approx 1.0278$ $y = \frac{1}{6} {11 + 4 \sqrt{7} + \frac{5 \sqrt{233 + 88 \sqrt{7}}}{7}} \approx 6.1666$
	Commented by nurtani last updated on 09/Jan/22

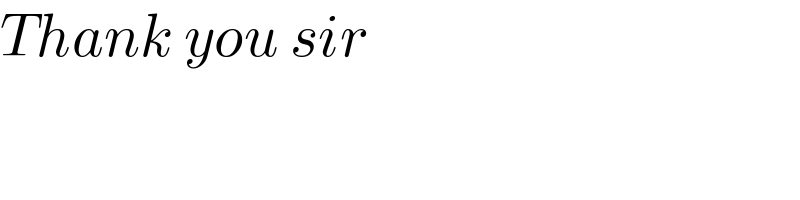
	$T h a n k y o u s i r$
	Commented by Tawa11 last updated on 09/Jan/22

	$Great sir$
	Answered by behi834171 last updated on 09/Jan/22

	$x \neq 0, y \neq 0$ $\frac{2}{\sqrt{3 x}} + \frac{4 \sqrt{2}}{\sqrt{7 y}} = 2 \Rightarrow \frac{2 \sqrt{2}}{\sqrt{7 y}} = 1 - \frac{1}{\sqrt{3 x}} \Rightarrow$ $\Rightarrow \frac{8}{7 y} = 1 - \frac{2}{\sqrt{3 x}} + \frac{1}{3 x} \Rightarrow y = \frac{8}{7 (1 - \frac{2}{\sqrt{3 x}} + \frac{1}{3 x})}$ $\Rightarrow \sqrt{3 x} (1 + \frac{1}{x + \frac{8}{7 (1 - \frac{2}{\sqrt{3 x}} + \frac{1}{3 x})}}) = 2 \overset{\frac{1}{\sqrt{3 x}} = m}{\Rightarrow}$ $\frac{1}{m} (1 + \frac{1}{\frac{1}{3 m^{2}} + \frac{8}{7 - 14 m + 7 m^{2}}}) = 2 \Rightarrow$ $\frac{1}{3 m^{2}} + \frac{8}{7 - 14 m + 7 m^{2}} = \frac{1}{2 m - 1} \Rightarrow$ $\frac{8}{7 - 14 m + 7 m^{2}} = \frac{3 m^{2} - 2 m + 1}{3 m^{2} (2 m - 1)} \Rightarrow$ $\Rightarrow 24 m^{2} (2 m - 1) = 7 (m^{2} - 2 m + 1) (3 m^{2} - 2 m + 1) \Rightarrow$ $\Rightarrow 48 m^{3} - 24 m^{2} = 7 (3 m^{4} - 8 m^{3} + 8 m^{2} - 4 m + 1) \Rightarrow$ $\Rightarrow 21 m^{4} - 104 m^{3} + 80 m^{2} - 28 m + 7 = 0$ $\Rightarrow m = 0.57, m = 4.1$ $\Rightarrow \frac{1}{3 x} = m^{2} \Rightarrow x = \frac{1}{3 m^{2}} \Rightarrow [x = 1.03, 0.021]$ $\Rightarrow \frac{8}{7 y} = 1 - 2 m + m^{2} \Rightarrow [y = 6.2, 0.12] . ◼$
	Commented by nurtani last updated on 09/Jan/22

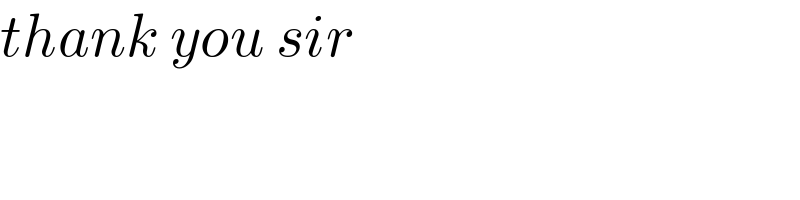
	$t h a n k y o u s i r$
	Commented by mr W last updated on 09/Jan/22

	$o n l y o n e s o l u t i o n f u l f i l l s t h e$ $o r i g i n a l e q u a t i o n s!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum