
Question and Answers Forum
Question Number 163854 by amin96 last updated on 11/Jan/22
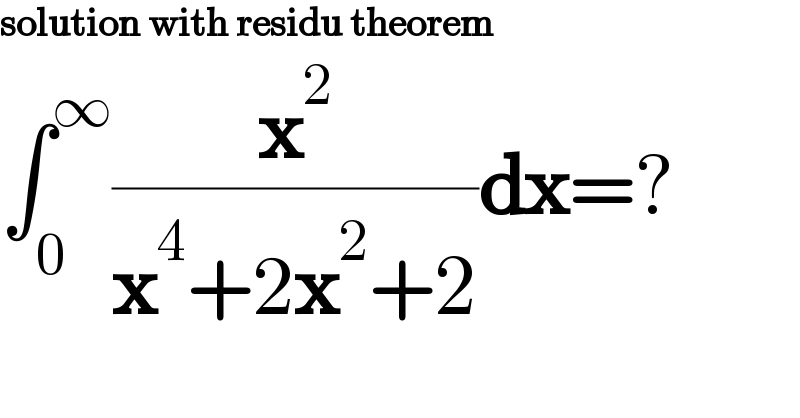
Answered by Ar Brandon last updated on 11/Jan/22
![I=∫_0 ^∞ (x^2 /(x^4 +2x^2 +2))dx=(1/2)∫_0 ^∞ (((x^2 +(√2))+(x^2 −(√2)))/(x^4 +2x^2 +2))dx =(1/2)∫_0 ^∞ ((x^2 +(√2))/(x^4 +2x^2 +2))dx+(1/2)∫_0 ^∞ ((x^2 −(√2))/(x^4 +2x^2 +2))dx =(1/2)∫_0 ^∞ ((1+((√2)/x^2 ))/(x^2 +2+(2/x^2 )))dx+(1/2)∫_0 ^∞ ((1−((√2)/x^2 ))/(x^2 +2+(2/x^2 )))dx =(1/2)∫_0 ^∞ ((1+((√2)/x^2 ))/((x−((√2)/x))^2 +2+2(√2)))dx+(1/2)∫_0 ^∞ ((1−((√2)/x^2 ))/((x+((√2)/x))^2 +2−2(√2)))dx =(1/2)∫_(−∞) ^(+∞) (du/(u^2 +(2+2(√2))))+(1/2)∫_(+∞) ^(+∞) (dv/(v^2 +2−2(√2))) =(1/2)∙(1/( (√(2+2(√2)))))[arctan((u/( (√(2+2(√2))))))]_(−∞) ^(+∞) =(π/(2(√(2+2(√2)))))](Q163864.png)
Commented by peter frank last updated on 11/Jan/22

Commented by amin96 last updated on 11/Jan/22
| ||
Question and Answers Forum | ||
Question Number 163854 by amin96 last updated on 11/Jan/22 | ||
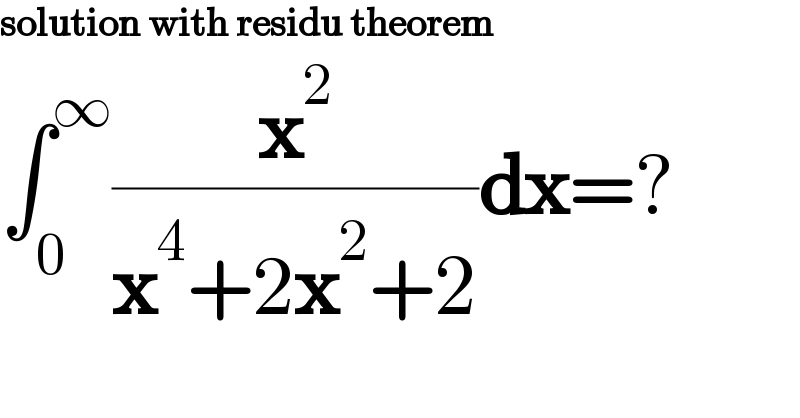 | ||
Answered by Ar Brandon last updated on 11/Jan/22 | ||
![I=∫_0 ^∞ (x^2 /(x^4 +2x^2 +2))dx=(1/2)∫_0 ^∞ (((x^2 +(√2))+(x^2 −(√2)))/(x^4 +2x^2 +2))dx =(1/2)∫_0 ^∞ ((x^2 +(√2))/(x^4 +2x^2 +2))dx+(1/2)∫_0 ^∞ ((x^2 −(√2))/(x^4 +2x^2 +2))dx =(1/2)∫_0 ^∞ ((1+((√2)/x^2 ))/(x^2 +2+(2/x^2 )))dx+(1/2)∫_0 ^∞ ((1−((√2)/x^2 ))/(x^2 +2+(2/x^2 )))dx =(1/2)∫_0 ^∞ ((1+((√2)/x^2 ))/((x−((√2)/x))^2 +2+2(√2)))dx+(1/2)∫_0 ^∞ ((1−((√2)/x^2 ))/((x+((√2)/x))^2 +2−2(√2)))dx =(1/2)∫_(−∞) ^(+∞) (du/(u^2 +(2+2(√2))))+(1/2)∫_(+∞) ^(+∞) (dv/(v^2 +2−2(√2))) =(1/2)∙(1/( (√(2+2(√2)))))[arctan((u/( (√(2+2(√2))))))]_(−∞) ^(+∞) =(π/(2(√(2+2(√2)))))](Q163864.png) | ||
| ||
Commented by peter frank last updated on 11/Jan/22 | ||
 | ||
Commented by amin96 last updated on 11/Jan/22 | ||
 | ||