Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 16392 by ajfour last updated on 21/Jun/17

Answered by Tinkutara last updated on 21/Jun/17

Commented by Tinkutara last updated on 21/Jun/17

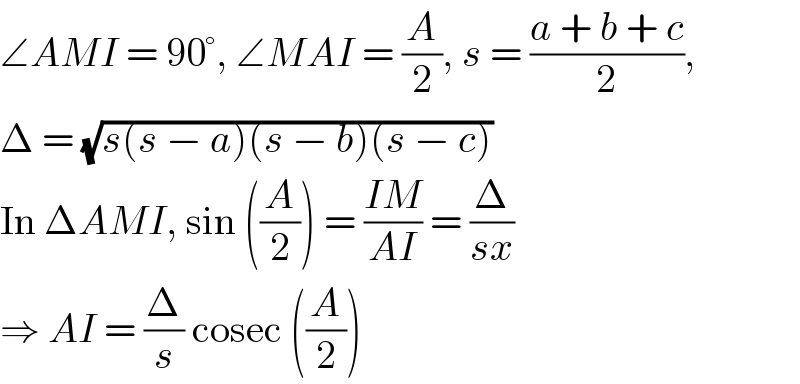
∠AMI = 90°, ∠MAI = (A/2), s = ((a + b + c)/2), Δ = (√(s(s − a)(s − b)(s − c))) In ΔAMI, sin ((A/2)) = ((IM)/(AI)) = (Δ/(sx)) ⇒ AI = (Δ/s) cosec ((A/2))

$$\angle{AMI}\:=\:\mathrm{90}°,\:\angle{MAI}\:=\:\frac{{A}}{\mathrm{2}},\:{s}\:=\:\frac{{a}\:+\:{b}\:+\:{c}}{\mathrm{2}}, \\ $$$$\Delta\:=\:\sqrt{{s}\left({s}\:−\:{a}\right)\left({s}\:−\:{b}\right)\left({s}\:−\:{c}\right)} \\ $$$$\mathrm{In}\:\Delta{AMI},\:\mathrm{sin}\:\left(\frac{{A}}{\mathrm{2}}\right)\:=\:\frac{{IM}}{{AI}}\:=\:\frac{\Delta}{{sx}} \\ $$$$\Rightarrow\:{AI}\:=\:\frac{\Delta}{{s}}\:\mathrm{cosec}\:\left(\frac{{A}}{\mathrm{2}}\right) \\ $$

Commented by Tinkutara last updated on 21/Jun/17

Commented by Tinkutara last updated on 21/Jun/17

[ABC] = [ABP] + [APC] (1/2)bc sin A = (1/2) c.AP sin ((A/2)) + (1/2)b.AP sin ((A/2)) bc sin A = AP (b + c) sin ((A/2)) AP = ((bc sin A)/((b + c) sin ((A/2)))) = ((2bc)/(b + c)) cos ((A/2)) ∴ IP = AP − AI can easily be calculated.

$$\left[{ABC}\right]\:=\:\left[{ABP}\right]\:+\:\left[{APC}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{bc}\:\mathrm{sin}\:{A}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{c}.{AP}\:\mathrm{sin}\:\left(\frac{{A}}{\mathrm{2}}\right) \\ $$$$+\:\frac{\mathrm{1}}{\mathrm{2}}{b}.{AP}\:\mathrm{sin}\:\left(\frac{{A}}{\mathrm{2}}\right) \\ $$$${bc}\:\mathrm{sin}\:{A}\:=\:{AP}\:\left({b}\:+\:{c}\right)\:\mathrm{sin}\:\left(\frac{{A}}{\mathrm{2}}\right) \\ $$$${AP}\:=\:\frac{{bc}\:\mathrm{sin}\:{A}}{\left({b}\:+\:{c}\right)\:\mathrm{sin}\:\left(\frac{{A}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{2}{bc}}{{b}\:+\:{c}}\:\mathrm{cos}\:\left(\frac{{A}}{\mathrm{2}}\right) \\ $$$$\therefore\:\boldsymbol{{IP}}\:=\:\boldsymbol{{AP}}\:−\:\boldsymbol{{AI}}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{be} \\ $$$$\mathrm{calculated}. \\ $$

Commented by ajfour last updated on 21/Jun/17

very good, thanks .

$${very}\:{good},\:{thanks}\:. \\ $$

Answered by mrW1 last updated on 21/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17

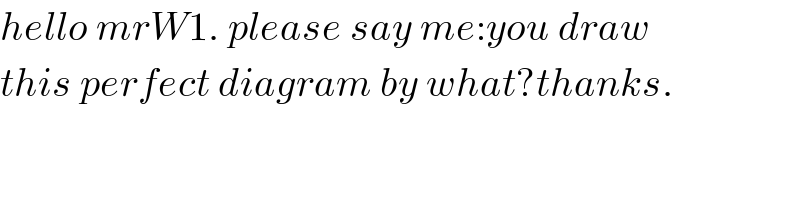
hello mrW1. please say me:you draw this perfect diagram by what?thanks.

$${hello}\:{mrW}\mathrm{1}.\:{please}\:{say}\:{me}:{you}\:{draw}\: \\ $$$${this}\:{perfect}\:{diagram}\:{by}\:{what}?{thanks}. \\ $$

Commented by mrW1 last updated on 22/Jun/17

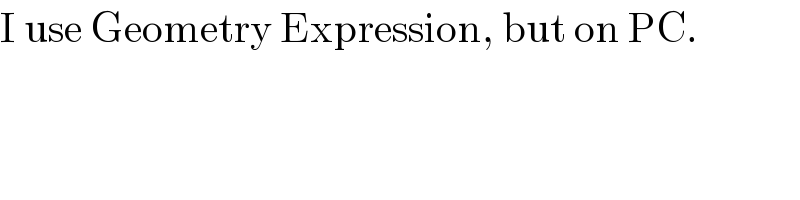
I use Geometry Expression, but on PC.

$$\mathrm{I}\:\mathrm{use}\:\mathrm{Geometry}\:\mathrm{Expression},\:\mathrm{but}\:\mathrm{on}\:\mathrm{PC}. \\ $$

Commented by mrW1 last updated on 21/Jun/17

let s=((a+b+c)/2) let Δ=area of ΔABC=(√(s(s−a)(s−b)(s−c))) u+v=c ...i v+w=a ...ii w+u=b ...iii sum of all: 2(u+v+w)=(a+b+c)=2s ⇒u+v+w=s ...iv (iv)−(i)⇒w=s−c (iv)−(ii)⇒u=s−a (iv)−(iii)⇒v=s−b x^2 =AI^2 =u^2 +r^2 =(s−a)^2 +[(Δ/s)]^2 =(s−a)^2 +((s(s−a)(s−b)(s−c))/s^2 ) =(s−a)[(s−a)+(((s−b)(s−c))/s)] =(s−a)[((2s^2 −s(a+b+c)+bc)/s)] =(s−a)[((2s^2 −2s^2 +bc)/s)] =(((s−a)bc)/s) ⇒x=(√(((s−a)bc)/s)) height of ΔABC over side BC= h_A (1/2)×a×h_A =Δ ⇒h_A =((2Δ)/a) r=(Δ/s) ⇒(h_A /r)=((2s)/a) ((AD)/(ID))=(h_A /r) ⇒((x+y)/y)=(h_A /r)=((2s)/a) ax+ay=2sy (2s−a)y=ax (b+c)y=ax ⇒y=(a/(b+c))x ⇒y=(a/(b+c))(√(((s−a)bc)/s))

$$\mathrm{let}\:\mathrm{s}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2}} \\ $$$$\mathrm{let}\:\Delta=\mathrm{area}\:\mathrm{of}\:\Delta\mathrm{ABC}=\sqrt{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)} \\ $$$$ \\ $$$$\mathrm{u}+\mathrm{v}=\mathrm{c}\:\:...\mathrm{i} \\ $$$$\mathrm{v}+\mathrm{w}=\mathrm{a}\:\:\:...\mathrm{ii} \\ $$$$\mathrm{w}+\mathrm{u}=\mathrm{b}\:\:\:...\mathrm{iii} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{all}: \\ $$$$\mathrm{2}\left(\mathrm{u}+\mathrm{v}+\mathrm{w}\right)=\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)=\mathrm{2s} \\ $$$$\Rightarrow\mathrm{u}+\mathrm{v}+\mathrm{w}=\mathrm{s}\:\:\:...\mathrm{iv} \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{i}\right)\Rightarrow\mathrm{w}=\mathrm{s}−\mathrm{c} \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{ii}\right)\Rightarrow\mathrm{u}=\mathrm{s}−\mathrm{a} \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{iii}\right)\Rightarrow\mathrm{v}=\mathrm{s}−\mathrm{b} \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{AI}^{\mathrm{2}} =\mathrm{u}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\left(\mathrm{s}−\mathrm{a}\right)^{\mathrm{2}} +\left[\frac{\Delta}{\mathrm{s}}\right]^{\mathrm{2}} \\ $$$$=\left(\mathrm{s}−\mathrm{a}\right)^{\mathrm{2}} +\frac{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}{\mathrm{s}^{\mathrm{2}} } \\ $$$$=\left(\mathrm{s}−\mathrm{a}\right)\left[\left(\mathrm{s}−\mathrm{a}\right)+\frac{\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}{\mathrm{s}}\right] \\ $$$$=\left(\mathrm{s}−\mathrm{a}\right)\left[\frac{\mathrm{2s}^{\mathrm{2}} −\mathrm{s}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)+\mathrm{bc}}{\mathrm{s}}\right] \\ $$$$=\left(\mathrm{s}−\mathrm{a}\right)\left[\frac{\mathrm{2s}^{\mathrm{2}} −\mathrm{2s}^{\mathrm{2}} +\mathrm{bc}}{\mathrm{s}}\right] \\ $$$$=\frac{\left(\mathrm{s}−\mathrm{a}\right)\mathrm{bc}}{\mathrm{s}} \\ $$$$\Rightarrow\mathrm{x}=\sqrt{\frac{\left(\mathrm{s}−\mathrm{a}\right)\mathrm{bc}}{\mathrm{s}}} \\ $$$$ \\ $$$$\mathrm{height}\:\mathrm{of}\:\Delta\mathrm{ABC}\:\mathrm{over}\:\mathrm{side}\:\mathrm{BC}=\:\mathrm{h}_{\mathrm{A}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{a}×\mathrm{h}_{\mathrm{A}} =\Delta \\ $$$$\Rightarrow\mathrm{h}_{\mathrm{A}} =\frac{\mathrm{2}\Delta}{\mathrm{a}} \\ $$$$\mathrm{r}=\frac{\Delta}{\mathrm{s}} \\ $$$$\Rightarrow\frac{\mathrm{h}_{\mathrm{A}} }{\mathrm{r}}=\frac{\mathrm{2s}}{\mathrm{a}} \\ $$$$ \\ $$$$\frac{\mathrm{AD}}{\mathrm{ID}}=\frac{\mathrm{h}_{\mathrm{A}} }{\mathrm{r}} \\ $$$$\Rightarrow\frac{\mathrm{x}+\mathrm{y}}{\mathrm{y}}=\frac{\mathrm{h}_{\mathrm{A}} }{\mathrm{r}}=\frac{\mathrm{2s}}{\mathrm{a}} \\ $$$$\mathrm{ax}+\mathrm{ay}=\mathrm{2sy} \\ $$$$\left(\mathrm{2s}−\mathrm{a}\right)\mathrm{y}=\mathrm{ax} \\ $$$$\left(\mathrm{b}+\mathrm{c}\right)\mathrm{y}=\mathrm{ax} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+\mathrm{c}}\mathrm{x} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{a}}{\mathrm{b}+\mathrm{c}}\sqrt{\frac{\left(\mathrm{s}−\mathrm{a}\right)\mathrm{bc}}{\mathrm{s}}} \\ $$

Commented by ajfour last updated on 22/Jun/17

thank you sir, very natural, loved reading the solution..

$$\:{thank}\:{you}\:{sir},\:{very}\:{natural},\:{loved} \\ $$$$\:{reading}\:{the}\:{solution}.. \\ $$

Commented by mrW1 last updated on 22/Jun/17

thank you too, sir! At first I always try to solve without using trigonomical formula which I can′t remember well.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{too},\:\mathrm{sir}! \\ $$$$\mathrm{At}\:\mathrm{first}\:\mathrm{I}\:\mathrm{always}\:\mathrm{try}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{without} \\ $$$$\mathrm{using}\:\mathrm{trigonomical}\:\mathrm{formula}\:\mathrm{which}\:\mathrm{I} \\ $$$$\mathrm{can}'\mathrm{t}\:\mathrm{remember}\:\mathrm{well}. \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17

((BD)/(DC))=(c/b)⇒((BD+DC)/(DC))=((b+c)/b)⇒DC=((ab)/(b+c)) ⇒ { ((BD=((ac)/(b+c)))),((DC=((ab)/(b+c)))) :} a(AD^2 +BD.DC)=b^2 .BD+c^2 .DC⇒ a(AD^2 +((a^2 bc)/((b+c)^2 )))=((acb^2 )/(b+c))+((abc^2 )/(b+c))(Estewart teorem) ⇒AD^2 +((a^2 bc)/((b+c)^2 ))= bc⇒AD^2 =bc−((a^2 bc)/((b+c)^2 )) AD^2 =bc((((b+c)^2 −a^2 )/((b+c)^2 )))=bc((2p.2(p−a))/((b+c)^2 )) ⇒AD=(2/(b+c))(√(bcp(p−a)))=((2bc)/(b+c)).cos(A/2) ((AI)/(sin(B/2)))=(c/(sin(180−((A+B)/2))))=(c/(cos(C/2)))⇒ AI=c.sin(B/2).sec(C/2)=c(√(((p−a)(p−c))/(ac))).(√((ba)/(p(p−c)))) ⇒AI=x=(√(bc.((p−a)/p))) (y/(sin(C/2)))=((DC)/(sin((A+C)/2)))=((DC)/(cos(B/2))) y=DC.sin(C/2).sec(B/2)=((ab)/(b+c))(√(((p−a)(p−b))/(ab))).(√((ac)/(p(p−b))))= =(a/(b+c))(√(bc.(((p−a))/p))) .■ note: ID=(a/(b+c))(√(bc.((p−a)/p))),AI=(√(bc.((p−a)/p))) IE=(b/(a+c))(√(ac.((p−b)/p))),BI=(√(ac.((p−b)/p))) IF=(c/(a+b))(√(ab.((p−c)/p))),CI=(√(ab.((p−c)/p)))

$$\frac{{BD}}{{DC}}=\frac{{c}}{{b}}\Rightarrow\frac{{BD}+{DC}}{{DC}}=\frac{{b}+{c}}{{b}}\Rightarrow{DC}=\frac{{ab}}{{b}+{c}} \\ $$$$\Rightarrow\begin{cases}{{BD}=\frac{{ac}}{{b}+{c}}}\\{{DC}=\frac{{ab}}{{b}+{c}}}\end{cases} \\ $$$${a}\left({AD}^{\mathrm{2}} +{BD}.{DC}\right)={b}^{\mathrm{2}} .{BD}+{c}^{\mathrm{2}} .{DC}\Rightarrow \\ $$$${a}\left({AD}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {bc}}{\left({b}+{c}\right)^{\mathrm{2}} }\right)=\frac{{acb}^{\mathrm{2}} }{{b}+{c}}+\frac{{abc}^{\mathrm{2}} }{{b}+{c}}\left({Estewart}\:{teorem}\right) \\ $$$$\Rightarrow{AD}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {bc}}{\left({b}+{c}\right)^{\mathrm{2}} }=\:{bc}\Rightarrow{AD}^{\mathrm{2}} ={bc}−\frac{{a}^{\mathrm{2}} {bc}}{\left({b}+{c}\right)^{\mathrm{2}} } \\ $$$${AD}^{\mathrm{2}} ={bc}\left(\frac{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{\left({b}+{c}\right)^{\mathrm{2}} }\right)={bc}\frac{\mathrm{2}{p}.\mathrm{2}\left({p}−{a}\right)}{\left({b}+{c}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{AD}=\frac{\mathrm{2}}{{b}+{c}}\sqrt{{bcp}\left({p}−{a}\right)}=\frac{\mathrm{2}{bc}}{{b}+{c}}.{cos}\frac{{A}}{\mathrm{2}} \\ $$$$\frac{{AI}}{{sin}\frac{{B}}{\mathrm{2}}}=\frac{{c}}{{sin}\left(\mathrm{180}−\frac{{A}+{B}}{\mathrm{2}}\right)}=\frac{{c}}{{cos}\frac{{C}}{\mathrm{2}}}\Rightarrow \\ $$$${AI}={c}.{sin}\frac{{B}}{\mathrm{2}}.{sec}\frac{{C}}{\mathrm{2}}={c}\sqrt{\frac{\left({p}−{a}\right)\left({p}−{c}\right)}{{ac}}}.\sqrt{\frac{{ba}}{{p}\left({p}−{c}\right)}} \\ $$$$\Rightarrow{AI}={x}=\sqrt{{bc}.\frac{{p}−{a}}{{p}}} \\ $$$$\frac{{y}}{{sin}\frac{{C}}{\mathrm{2}}}=\frac{{DC}}{{sin}\frac{{A}+{C}}{\mathrm{2}}}=\frac{{DC}}{{cos}\frac{{B}}{\mathrm{2}}} \\ $$$${y}={DC}.{sin}\frac{{C}}{\mathrm{2}}.{sec}\frac{{B}}{\mathrm{2}}=\frac{{ab}}{{b}+{c}}\sqrt{\frac{\left({p}−{a}\right)\left({p}−{b}\right)}{{ab}}}.\sqrt{\frac{{ac}}{{p}\left({p}−{b}\right)}}= \\ $$$$=\frac{{a}}{{b}+{c}}\sqrt{{bc}.\frac{\left({p}−{a}\right)}{{p}}}\:\:\:\:.\blacksquare \\ $$$${note}: \\ $$$${ID}=\frac{{a}}{{b}+{c}}\sqrt{{bc}.\frac{{p}−{a}}{{p}}},{AI}=\sqrt{{bc}.\frac{{p}−{a}}{{p}}} \\ $$$${IE}=\frac{{b}}{{a}+{c}}\sqrt{{ac}.\frac{{p}−{b}}{{p}}},{BI}=\sqrt{{ac}.\frac{{p}−{b}}{{p}}} \\ $$$${IF}=\frac{{c}}{{a}+{b}}\sqrt{{ab}.\frac{{p}−{c}}{{p}}},{CI}=\sqrt{{ab}.\frac{{p}−{c}}{{p}}} \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17

great thank to you dear mr Ajfour.

$${great}\:{thank}\:{to}\:{you}\:{dear}\:{mr}\:{Ajfour}. \\ $$

Commented by ajfour last updated on 22/Jun/17

I am very grateful to you sir, utterly complete an analysis this is.

$${I}\:{am}\:{very}\:{grateful}\:{to}\:{you}\:{sir}, \\ $$$$\:{utterly}\:{complete}\:{an}\:{analysis}\:{this}\:{is}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com