
Question and Answers Forum
Question Number 163921 by ajfour last updated on 11/Jan/22

Answered by mr W last updated on 12/Jan/22
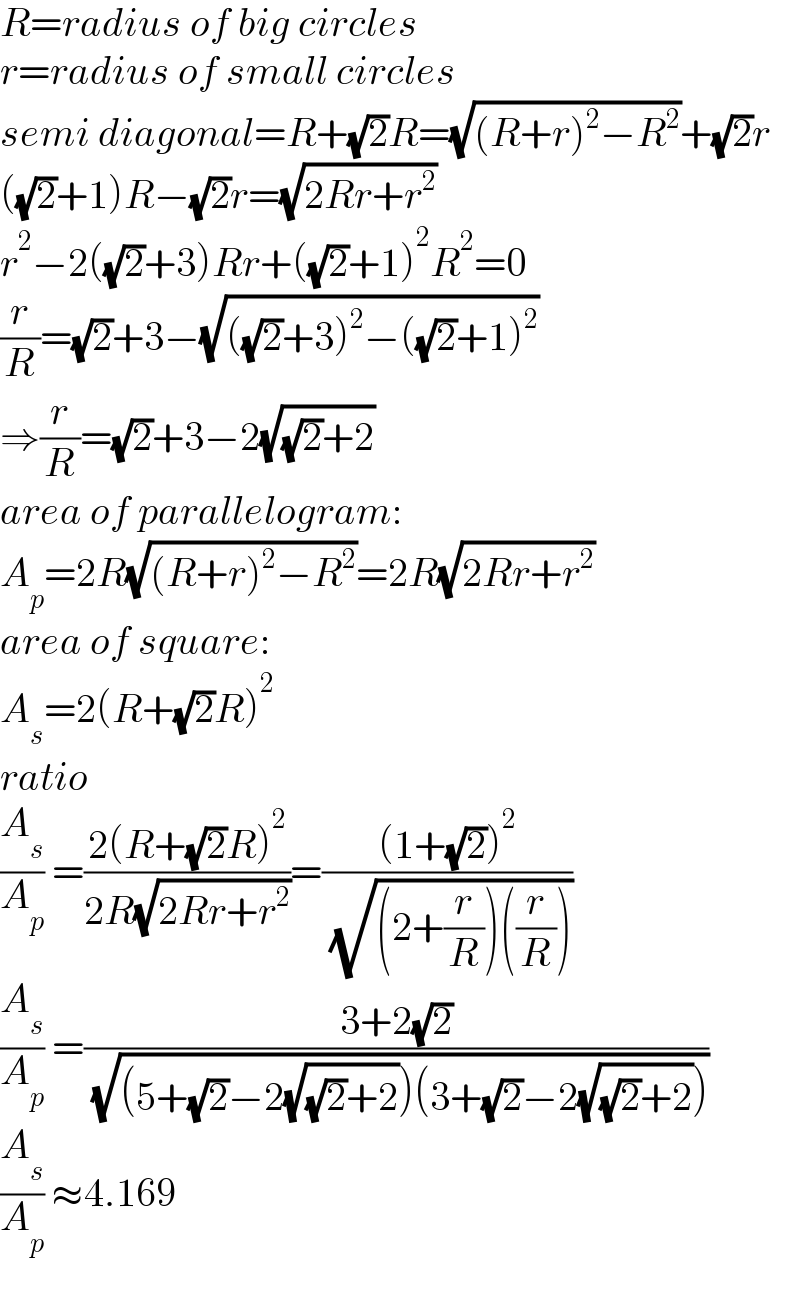
Commented by Tawa11 last updated on 12/Jan/22

Answered by ajfour last updated on 12/Jan/22
![R+R(√2)=s(√2) R+r+2(√(Rr))=2s (√(r/R))+1=(√((2s)/R)) R=(2−(√2))s r=R((√(2/(2−(√2))))−1)^2 =R((√(2+(√2)))−1)^2 A_p =4R(√((r+R)^2 −R^2 )) =(4s^2 )(2−(√2))^2 {[((√(2+(√2)))−1)^2 +1]^2 −1}^(1/2) (A_p /A_s )=(2−(√2))^2 {[((√(2+(√2)))−1)^2 +1]^2 −1}^(1/2) ...](Q164000.png)
| ||
Question and Answers Forum | ||
Question Number 163921 by ajfour last updated on 11/Jan/22 | ||
 | ||
Answered by mr W last updated on 12/Jan/22 | ||
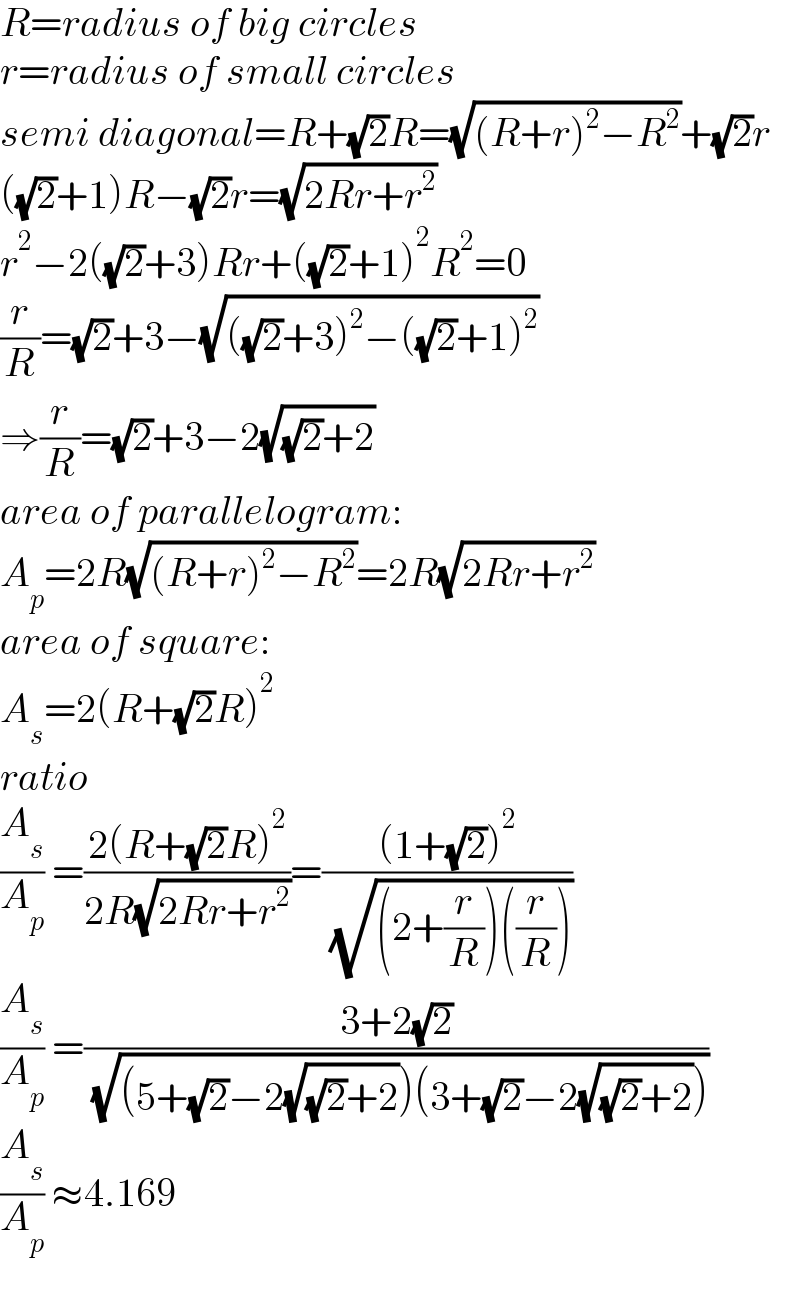 | ||
| ||
Commented by Tawa11 last updated on 12/Jan/22 | ||
 | ||
Answered by ajfour last updated on 12/Jan/22 | ||
![R+R(√2)=s(√2) R+r+2(√(Rr))=2s (√(r/R))+1=(√((2s)/R)) R=(2−(√2))s r=R((√(2/(2−(√2))))−1)^2 =R((√(2+(√2)))−1)^2 A_p =4R(√((r+R)^2 −R^2 )) =(4s^2 )(2−(√2))^2 {[((√(2+(√2)))−1)^2 +1]^2 −1}^(1/2) (A_p /A_s )=(2−(√2))^2 {[((√(2+(√2)))−1)^2 +1]^2 −1}^(1/2) ...](Q164000.png) | ||
| ||