Question Number 164073 by mr W last updated on 13/Jan/22
Commented by mr W last updated on 13/Jan/22
$${are}\:{there}\:{other}\:{equilibrium}\:{positions} \\ $$$${for}\:{the}\:{rod}? \\ $$
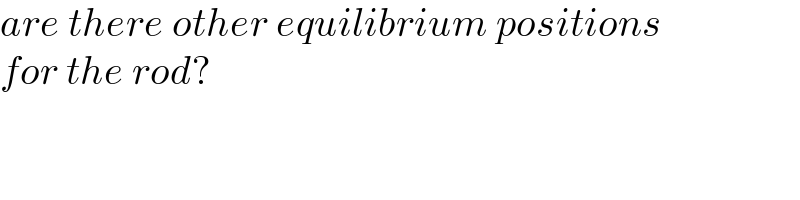
Answered by ajfour last updated on 13/Jan/22
Commented by mr W last updated on 14/Jan/22
$${no}\:{sir}.\:{i}\:{mean}\:{it}\:{should}\:{be}\:{possible} \\ $$$${that}\:{the}\:{three}\:{forces}\:{on}\:{the}\:{rod}\:{are} \\ $$$${in}\:{equilibrium}\:{in}\:{a}\:{way}\:{without}\: \\ $$$${friction}\:{like}\:{this}: \\ $$
Commented by mr W last updated on 14/Jan/22
$${according}\:{to}\:{our}\:{experience}\:{in}\:{real} \\ $$$${life},\:{the}\:{rod}\:{can}\:{also}\:{rest}\:{in}\:{the}\:{bowl} \\ $$$${in}\:{a}\:{inclined}\:{position},\:{which}\:{is}\:{even} \\ $$$${more}\:{stable}.\:{in}\:{fact}\:{the}\:{horizontal}\: \\ $$$${position}\:{is}\:{even}\:{instable},\:{because}\:{we}\: \\ $$$${can}\:{hardly}\:{bring}\:{the}\:{rod}\:{to}\:{rest}\:{in}\:{a}\: \\ $$$${horizontal}\:{position}.\:{but}\:{we}\:{only}\:{need} \\ $$$${to}\:{release}\:{the}\:{rod}\:{in}\:{the}\:{bowl},\:{it}\:{will}\: \\ $$$${come}\:{to}\:{rest}\:{by}\:{itself}\:{in}\:{an}\:{inclined}\: \\ $$$${position}. \\ $$
Commented by ajfour last updated on 13/Jan/22
$${friction}\:{need}\:{be}\:{there},\:{then}\:{only} \\ $$$${it}\:{can}\:{rest}\:{in}\:{inclined}\:{way}\:{is}\:{what} \\ $$$${i}\:{conclude},\:{is}\:{that}\:{what}\:{you}\:{too}\: \\ $$$${mean},\:{sir}? \\ $$
Commented by mr W last updated on 14/Jan/22
Answered by mr W last updated on 14/Jan/22
Commented by mr W last updated on 14/Jan/22
![parabola y=(x^2 /a) with a=1 here length of rod is b. C=center of mass there are three forces acting on rod: normal contact forces N_1 and N_2 , and gravity of rod mg when the rod is in equilibrium, all these three forces must intersect at one point S. say the end points of the rod are A(p, (p^2 /a)), B(q, (q^2 /a)) tan φ=−(dy/dx)∣_(x=p) =−((2p)/a) tan ϕ=(dy/dx)∣_(x=q) =((2q)/a) tan θ=(((q^2 /a)−(p^2 /a))/(q−p))=((q^2 −p^2 )/(a(q−p)))=((q+p)/a) α=(π/2)−φ−θ β=(π/2)−ϕ+θ ((SC)/(AC))=((sin α)/(sin φ))=((sin ((π/2)−φ−θ))/(sin φ))=((cos (φ+θ))/(sin φ)) ((SC)/(CB))=((sin β)/(sin ϕ))=((sin ((π/2)−ϕ+θ))/(sin ϕ))=((cos (ϕ−θ))/(sin ϕ)) since AC=CB=(b/2), ((cos (φ+θ))/(sin φ))=((cos (ϕ−θ))/(sin ϕ)) ((cos φ cos θ−sin φ sin θ)/(sin φ))=((cos ϕ cos θ+sin ϕ sin θ)/(sin ϕ)) ((cos θ)/(tan φ))−sin θ=((cos θ)/(tan ϕ))+sin θ (1/(tan φ))−(1/(tan ϕ))=2 tan θ −(a/(2p))−(a/(2q))=((2(p+q))/a) −((p+q)/(pq))=((4(p+q))/a^2 ) ⇒p+q=0 ⇒p=−q ⇒horizontal position or −(1/(pq))=(4/a^2 ) ⇒pq=−(a^2 /4) or (−p)q=(a^2 /4) (q−p)^2 +((q^2 /a)−(p^2 /a))^2 =b^2 (q−p)^2 +(((q−p)^2 (q+p)^2 )/a^2 )=b^2 (q−p)^2 [1+(((q+p)^2 )/a^2 )]=b^2 (q−p)^2 [1+(((q−p)^2 −4(−p)q)/a^2 )]=b^2 (q−p)^2 [1+(((q−p)^2 −a^2 )/a^2 )]=b^2 (q−p)^4 =a^2 b^2 ⇒q−p=(√(ab)) q and −p are roots of z^2 −(√(ab))z+(a^2 /4)=0 ⇒−p=(((√(ab))−(√(a(b−a))))/2) ⇒p=−(((√(ab))−(√(a(b−a))))/2) ⇒q=(((√(ab))+(√(a(b−a))))/2) that means generally there exist two possible equilibrium positions for a rod in a bowl: position 1: horizontal q=−p=(b/2) position 2: inclined p=−(((√(ab))−(√(a(b−a))))/2) q=(((√(ab))+(√(a(b−a))))/2) only for a short rod with b≤a, the horizontal position is the only possible equilibrium position.](Q164104.png)
$${parabola}\:{y}=\frac{{x}^{\mathrm{2}} }{{a}}\:{with}\:{a}=\mathrm{1}\:{here} \\ $$$${length}\:{of}\:{rod}\:{is}\:{b}. \\ $$$${C}={center}\:{of}\:{mass} \\ $$$${there}\:{are}\:{three}\:{forces}\:{acting}\:{on}\:{rod}: \\ $$$${normal}\:{contact}\:{forces}\:{N}_{\mathrm{1}} \:{and}\:{N}_{\mathrm{2}} , \\ $$$${and}\:{gravity}\:{of}\:{rod}\:{mg} \\ $$$${when}\:{the}\:{rod}\:{is}\:{in}\:{equilibrium},\:{all} \\ $$$${these}\:{three}\:{forces}\:{must}\:{intersect}\:{at} \\ $$$${one}\:{point}\:{S}. \\ $$$${say}\:{the}\:{end}\:{points}\:{of}\:{the}\:{rod}\:{are} \\ $$$${A}\left({p},\:\frac{{p}^{\mathrm{2}} }{{a}}\right),\:{B}\left({q},\:\frac{{q}^{\mathrm{2}} }{{a}}\right) \\ $$$$\mathrm{tan}\:\phi=−\frac{{dy}}{{dx}}\mid_{{x}={p}} =−\frac{\mathrm{2}{p}}{{a}} \\ $$$$\mathrm{tan}\:\varphi=\frac{{dy}}{{dx}}\mid_{{x}={q}} =\frac{\mathrm{2}{q}}{{a}} \\ $$$$\mathrm{tan}\:\theta=\frac{\frac{{q}^{\mathrm{2}} }{{a}}−\frac{{p}^{\mathrm{2}} }{{a}}}{{q}−{p}}=\frac{{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{{a}\left({q}−{p}\right)}=\frac{{q}+{p}}{{a}} \\ $$$$\alpha=\frac{\pi}{\mathrm{2}}−\phi−\theta \\ $$$$\beta=\frac{\pi}{\mathrm{2}}−\varphi+\theta \\ $$$$\frac{{SC}}{{AC}}=\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\phi}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\phi−\theta\right)}{\mathrm{sin}\:\phi}=\frac{\mathrm{cos}\:\left(\phi+\theta\right)}{\mathrm{sin}\:\phi} \\ $$$$\frac{{SC}}{{CB}}=\frac{\mathrm{sin}\:\beta}{\mathrm{sin}\:\varphi}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\varphi+\theta\right)}{\mathrm{sin}\:\varphi}=\frac{\mathrm{cos}\:\left(\varphi−\theta\right)}{\mathrm{sin}\:\varphi} \\ $$$${since}\:{AC}={CB}=\frac{{b}}{\mathrm{2}}, \\ $$$$\frac{\mathrm{cos}\:\left(\phi+\theta\right)}{\mathrm{sin}\:\phi}=\frac{\mathrm{cos}\:\left(\varphi−\theta\right)}{\mathrm{sin}\:\varphi} \\ $$$$\frac{\mathrm{cos}\:\phi\:\mathrm{cos}\:\theta−\mathrm{sin}\:\phi\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\phi}=\frac{\mathrm{cos}\:\varphi\:\mathrm{cos}\:\theta+\mathrm{sin}\:\varphi\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\varphi} \\ $$$$\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\phi}−\mathrm{sin}\:\theta=\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\varphi}+\mathrm{sin}\:\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\phi}−\frac{\mathrm{1}}{\mathrm{tan}\:\varphi}=\mathrm{2}\:\mathrm{tan}\:\theta \\ $$$$−\frac{{a}}{\mathrm{2}{p}}−\frac{{a}}{\mathrm{2}{q}}=\frac{\mathrm{2}\left({p}+{q}\right)}{{a}} \\ $$$$−\frac{{p}+{q}}{{pq}}=\frac{\mathrm{4}\left({p}+{q}\right)}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{p}+{q}=\mathrm{0}\:\Rightarrow{p}=−{q}\:\Rightarrow{horizontal}\:{position} \\ $$$${or} \\ $$$$−\frac{\mathrm{1}}{{pq}}=\frac{\mathrm{4}}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{pq}=−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\:{or}\:\left(−{p}\right){q}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\left({q}−{p}\right)^{\mathrm{2}} +\left(\frac{{q}^{\mathrm{2}} }{{a}}−\frac{{p}^{\mathrm{2}} }{{a}}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\left({q}−{p}\right)^{\mathrm{2}} +\frac{\left({q}−{p}\right)^{\mathrm{2}} \left({q}+{p}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }={b}^{\mathrm{2}} \\ $$$$\left({q}−{p}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\left({q}+{p}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right]={b}^{\mathrm{2}} \\ $$$$\left({q}−{p}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\left({q}−{p}\right)^{\mathrm{2}} −\mathrm{4}\left(−{p}\right){q}}{{a}^{\mathrm{2}} }\right]={b}^{\mathrm{2}} \\ $$$$\left({q}−{p}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\left({q}−{p}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right]={b}^{\mathrm{2}} \\ $$$$\left({q}−{p}\right)^{\mathrm{4}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow{q}−{p}=\sqrt{{ab}} \\ $$$${q}\:{and}\:−{p}\:{are}\:{roots}\:{of} \\ $$$${z}^{\mathrm{2}} −\sqrt{{ab}}{z}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow−{p}=\frac{\sqrt{{ab}}−\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow{p}=−\frac{\sqrt{{ab}}−\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow{q}=\frac{\sqrt{{ab}}+\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$${that}\:{means}\:{generally}\:{there}\:{exist}\: \\ $$$${two}\:{possible}\:{equilibrium}\:{positions}\: \\ $$$${for}\:{a}\:{rod}\:{in}\:{a}\:{bowl}: \\ $$$${position}\:\mathrm{1}:\:{horizontal}\: \\ $$$$\:\:\:\:\:\:\:{q}=−{p}=\frac{{b}}{\mathrm{2}} \\ $$$${position}\:\mathrm{2}:\:{inclined} \\ $$$$\:\:\:\:\:\:{p}=−\frac{\sqrt{{ab}}−\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{q}=\frac{\sqrt{{ab}}+\sqrt{{a}\left({b}−{a}\right)}}{\mathrm{2}} \\ $$$${only}\:{for}\:{a}\:{short}\:{rod}\:{with}\:{b}\leqslant{a},\:{the} \\ $$$${horizontal}\:{position}\:{is}\:{the}\:{only} \\ $$$${possible}\:{equilibrium}\:{position}. \\ $$
Commented by mr W last updated on 14/Jan/22
Commented by mr W last updated on 14/Jan/22
Commented by ajfour last updated on 14/Jan/22
$${excellent},\:{thank}\:{you}\:{sir}. \\ $$$${I}\:{shall}\:{attempt}\:{too}.. \\ $$
Commented by Tawa11 last updated on 15/Jan/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 17/Jan/22
Commented by mr W last updated on 16/Jan/22
$${we}\:{see}\:{that}\:{the}\:{inclined}\:{equilibrium} \\ $$$${position}\:{of}\:{the}\:{rod}\:{is}\:{the}\:{position} \\ $$$${where}\:{the}\:{center}\:{of}\:{mass}\:{of}\:{the}\:{rod} \\ $$$${is}\:{lowest}.\:{therefore}\:{it}'{s}\:{also}\:\:{the}\:{most} \\ $$$${stable}\:{position}. \\ $$$${see}\:{also}\:{Q}\mathrm{164178}. \\ $$
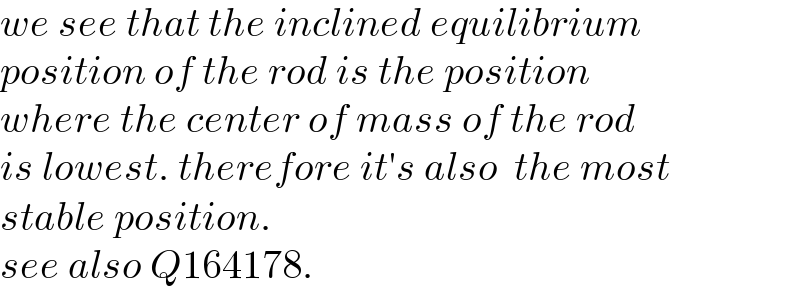
Commented by ajfour last updated on 16/Jan/22
$${This}\:{is}\:{really}\:{really}\:{Excellent}\:{sol}^{{n}} \:{sir}. \\ $$
Commented by mr W last updated on 16/Jan/22
$${thanks}\:{for}\:{reviewing}\:{sir}! \\ $$
Commented by mr W last updated on 17/Jan/22
$${interesting}: \\ $$$${at}\:{equilibrium}\:{positions},\:{we}\:{always} \\ $$$${have}\:{SA}\bot{SB}. \\ $$