Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 164305 by ajfour last updated on 16/Jan/22

Commented by ajfour last updated on 16/Jan/22

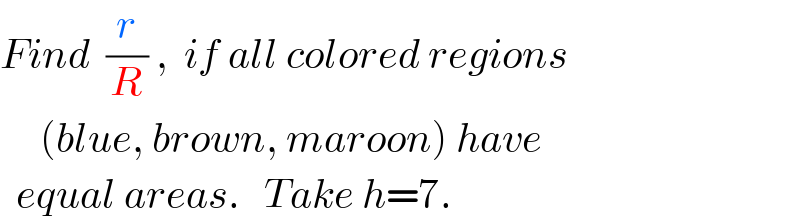
Find (r/R) , if all colored regions (blue, brown, maroon) have equal areas. Take h=7.

$${Find}\:\:\frac{{r}}{{R}}\:,\:\:{if}\:{all}\:{colored}\:{regions} \\ $$$$\:\:\:\:\:\left({blue},\:{brown},\:{maroon}\right)\:{have} \\ $$$$\:\:{equal}\:{areas}.\:\:\:{Take}\:{h}=\mathrm{7}. \\ $$

Answered by mr W last updated on 16/Jan/22

Commented by mr W last updated on 16/Jan/22

area of each region is ((h×1)/3)=(h/3) (((R+(√(R^2 −(b^2 /4)))−1)/(R+(√(R^2 −(b^2 /4))))))^2 =(1/2) ((R+(√(R^2 −(b^2 /4)))−1)/(R+(√(R^2 −(b^2 /4)))))=(1/( (√2))) (1/(R+(√(R^2 −(b^2 /4)))))=1−(1/( (√2)))=(((√2)−1)/( (√2))) R+(√(R^2 −(b^2 /4)))=((√2)/( (√2)−1))=2+(√2) (√(R^2 −(b^2 /4)))=2+(√2)−R R^2 −(b^2 /4)=(2+(√2))^2 +R^2 −2(2+(√2))R (2+(√2))^2 +(b^2 /4)=2(2+(√2))R ⇒R=1+((√2)/2)+(((2−(√2))b^2 )/(16)) ...(i) (b/2)×(R+(√(R^2 −(b^2 /4))))=2×(h/3) ⇒b(R+(√(R^2 −(b^2 /4))))=((4h)/3) ...(ii) ((R+(√(R^2 −(b^2 /4)))−1−r)/r)=((2(√([R+(√(R^2 −(b^2 /4)))]^2 +(b^2 /4))))/b) ((R+(√(R^2 −(b^2 /4)))−1)/r)=1+((2(√(2R(R+(√(R^2 −(b^2 /4)))))))/( b)) ⇒r=((R+(√(R^2 −(b^2 /4)))−1)/(1+((2(√(2R(R+(√(R^2 −(b^2 /4)))))))/b))) ...(iii) example: h=7 ⇒b≈2.7337 ⇒R≈1.9807 ⇒r≈0.6542

$${area}\:{of}\:{each}\:{region}\:{is}\:\frac{{h}×\mathrm{1}}{\mathrm{3}}=\frac{{h}}{\mathrm{3}} \\ $$$$\left(\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}=\mathrm{2}+\sqrt{\mathrm{2}}−{R} \\ $$$${R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){R} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){R} \\ $$$$\Rightarrow{R}=\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){b}^{\mathrm{2}} }{\mathrm{16}}\:\:\:...\left({i}\right) \\ $$$$\frac{{b}}{\mathrm{2}}×\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)=\mathrm{2}×\frac{{h}}{\mathrm{3}} \\ $$$$\Rightarrow{b}\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)=\frac{\mathrm{4}{h}}{\mathrm{3}}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$$\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}−{r}}{{r}}=\frac{\mathrm{2}\sqrt{\left[{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right]^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}{{b}} \\ $$$$\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{{r}}=\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{2}{R}\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)}}{\:{b}} \\ $$$$\Rightarrow{r}=\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{2}{R}\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)}}{{b}}}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$${example}:\:{h}=\mathrm{7} \\ $$$$\Rightarrow{b}\approx\mathrm{2}.\mathrm{7337} \\ $$$$\Rightarrow{R}\approx\mathrm{1}.\mathrm{9807} \\ $$$$\Rightarrow{r}\approx\mathrm{0}.\mathrm{6542} \\ $$

Commented by mr W last updated on 16/Jan/22

Commented by mr W last updated on 16/Jan/22

check: b=2.7337 R=1.9807 (√(R^2 −((b/2))^2 ))=1.4335 area of big triangle =((2.7337×(1.9807+1.4335))/2)=4.6667 =(7/3)×2 ✓ area of small triangle =4.6667×(((1.9807+1.4335−1)/(1.9807+1.4335)))^2 =2.3333 =(7/3) ✓

$${check}: \\ $$$${b}=\mathrm{2}.\mathrm{7337} \\ $$$${R}=\mathrm{1}.\mathrm{9807} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{1}.\mathrm{4335} \\ $$$${area}\:{of}\:{big}\:{triangle} \\ $$$$=\frac{\mathrm{2}.\mathrm{7337}×\left(\mathrm{1}.\mathrm{9807}+\mathrm{1}.\mathrm{4335}\right)}{\mathrm{2}}=\mathrm{4}.\mathrm{6667} \\ $$$$=\frac{\mathrm{7}}{\mathrm{3}}×\mathrm{2}\:\checkmark \\ $$$${area}\:{of}\:{small}\:{triangle} \\ $$$$=\mathrm{4}.\mathrm{6667}×\left(\frac{\mathrm{1}.\mathrm{9807}+\mathrm{1}.\mathrm{4335}−\mathrm{1}}{\mathrm{1}.\mathrm{9807}+\mathrm{1}.\mathrm{4335}}\right)^{\mathrm{2}} =\mathrm{2}.\mathrm{3333} \\ $$$$=\frac{\mathrm{7}}{\mathrm{3}}\:\checkmark \\ $$

Commented by ajfour last updated on 16/Jan/22

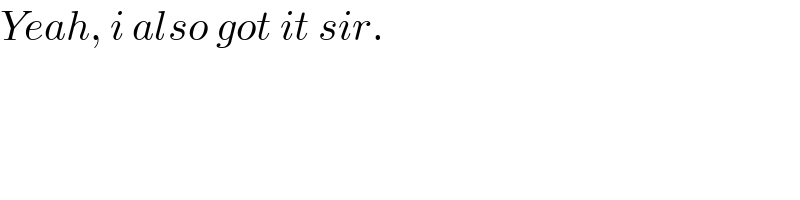
Yeah, i also got it sir.

$${Yeah},\:{i}\:{also}\:{got}\:{it}\:{sir}. \\ $$

Commented by Tawa11 last updated on 16/Jan/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 16/Jan/22

Commented by ajfour last updated on 16/Jan/22

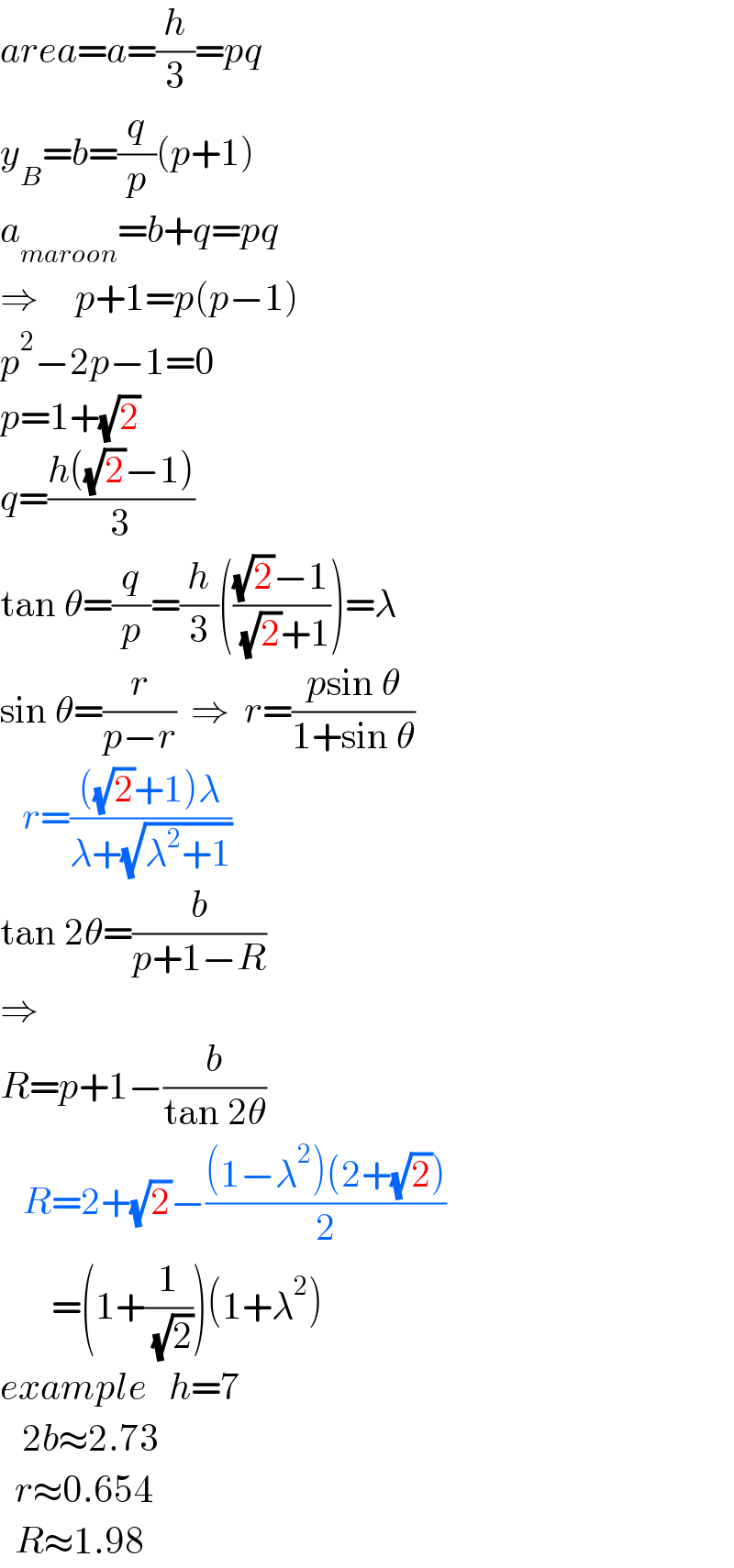
area=a=(h/3)=pq y_B =b=(q/p)(p+1) a_(maroon) =b+q=pq ⇒ p+1=p(p−1) p^2 −2p−1=0 p=1+(√2) q=((h((√2)−1))/3) tan θ=(q/p)=(h/3)((((√2)−1)/( (√2)+1)))=λ sin θ=(r/(p−r)) ⇒ r=((psin θ)/(1+sin θ)) r=((((√2)+1)λ)/(λ+(√(λ^2 +1)))) tan 2θ=(b/(p+1−R)) ⇒ R=p+1−(b/(tan 2θ)) R=2+(√2)−(((1−λ^2 )(2+(√2)))/2) =(1+(1/( (√2))))(1+λ^2 ) example h=7 2b≈2.73 r≈0.654 R≈1.98

$${area}={a}=\frac{{h}}{\mathrm{3}}={pq} \\ $$$${y}_{{B}} ={b}=\frac{{q}}{{p}}\left({p}+\mathrm{1}\right) \\ $$$${a}_{{maroon}} ={b}+{q}={pq}\:\:\:\: \\ $$$$\Rightarrow\:\:\:\:\:{p}+\mathrm{1}={p}\left({p}−\mathrm{1}\right) \\ $$$${p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{1}=\mathrm{0} \\ $$$${p}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$${q}=\frac{{h}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\theta=\frac{{q}}{{p}}=\frac{{h}}{\mathrm{3}}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right)=\lambda \\ $$$$\mathrm{sin}\:\theta=\frac{{r}}{{p}−{r}}\:\:\Rightarrow\:\:{r}=\frac{{p}\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta} \\ $$$$\:\:\:{r}=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\lambda}{\lambda+\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{tan}\:\mathrm{2}\theta=\frac{{b}}{{p}+\mathrm{1}−{R}} \\ $$$$\Rightarrow \\ $$$${R}={p}+\mathrm{1}−\frac{{b}}{\mathrm{tan}\:\mathrm{2}\theta} \\ $$$$\:\:\:{R}=\mathrm{2}+\sqrt{\mathrm{2}}−\frac{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\left(\mathrm{1}+\lambda^{\mathrm{2}} \right) \\ $$$${example}\:\:\:{h}=\mathrm{7} \\ $$$$\:\:\:\mathrm{2}{b}\approx\mathrm{2}.\mathrm{73} \\ $$$$\:\:{r}\approx\mathrm{0}.\mathrm{654} \\ $$$$\:\:{R}\approx\mathrm{1}.\mathrm{98} \\ $$

Commented by mr W last updated on 16/Jan/22

perfect! better than my solution which delivers only approximated result.

$${perfect}!\:{better}\:{than}\:{my}\:{solution}\:{which} \\ $$$${delivers}\:{only}\:{approximated}\:{result}. \\ $$

Commented by Tawa11 last updated on 16/Jan/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com