Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 164544 by mr W last updated on 18/Jan/22

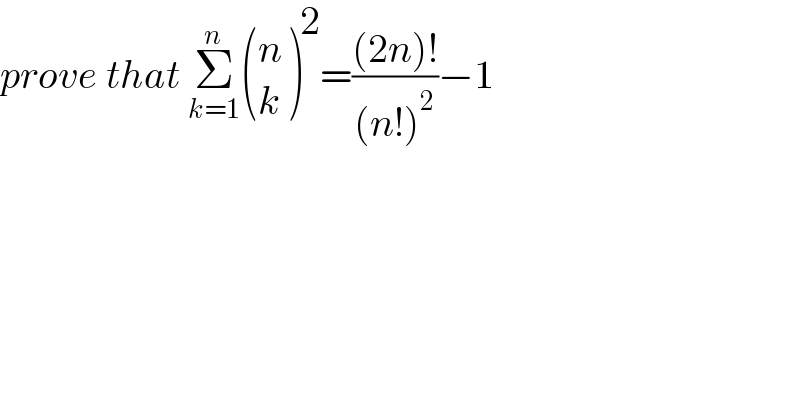
prove that Σ_(k=1) ^n ((n),(k) )^2 =(((2n)!)/((n!)^2 ))−1

$${prove}\:{that}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} =\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} }−\mathrm{1} \\ $$

Answered by mindispower last updated on 18/Jan/22

=Σ_(k=0) ^n ((n),(k) )−1 =Σ_(k=0) ^n ((n),(k) ) ((n),((n−k)) ) Σ_(k=0) ^(2n) (((2n)),(k) )x^k =(1+x)^(2n) =(1+x)^n (1+x)^n =Σ_(k=0) ^n Σ_(j=0) ^n ((n),(k) ) ((n),((n−j)) )x^(n+k−j) coeficient of x^n =Σ_(k=0) ^n ((n),(k) ) ((n),((n−k)) )= (((2n)),(n) ) S= (((2n)),(n) )−1=(((2n)!)/((n!)^2 ))−1

$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}−\mathrm{1} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\begin{pmatrix}{{n}}\\{{n}−{k}}\end{pmatrix} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{{k}}\end{pmatrix}{x}^{{k}} =\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} =\left(\mathrm{1}+{x}\right)^{{n}} \left(\mathrm{1}+{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\begin{pmatrix}{{n}}\\{{n}−{j}}\end{pmatrix}{x}^{{n}+{k}−{j}} \\ $$$${coeficient}\:{of}\:{x}^{{n}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\begin{pmatrix}{{n}}\\{{n}−{k}}\end{pmatrix}=\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix} \\ $$$${S}=\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}−\mathrm{1}=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} }−\mathrm{1} \\ $$$$ \\ $$

Commented by mr W last updated on 18/Jan/22

thanks alot sir!

$${thanks}\:{alot}\:{sir}! \\ $$

Commented by mindispower last updated on 18/Jan/22

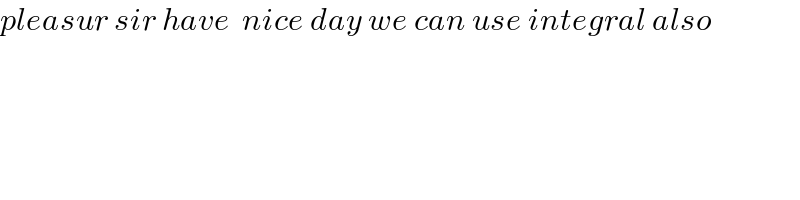
pleasur sir have nice day we can use integral also

$${pleasur}\:{sir}\:{have}\:\:{nice}\:{day}\:{we}\:{can}\:{use}\:{integral}\:{also} \\ $$

Answered by mindispower last updated on 19/Jan/22

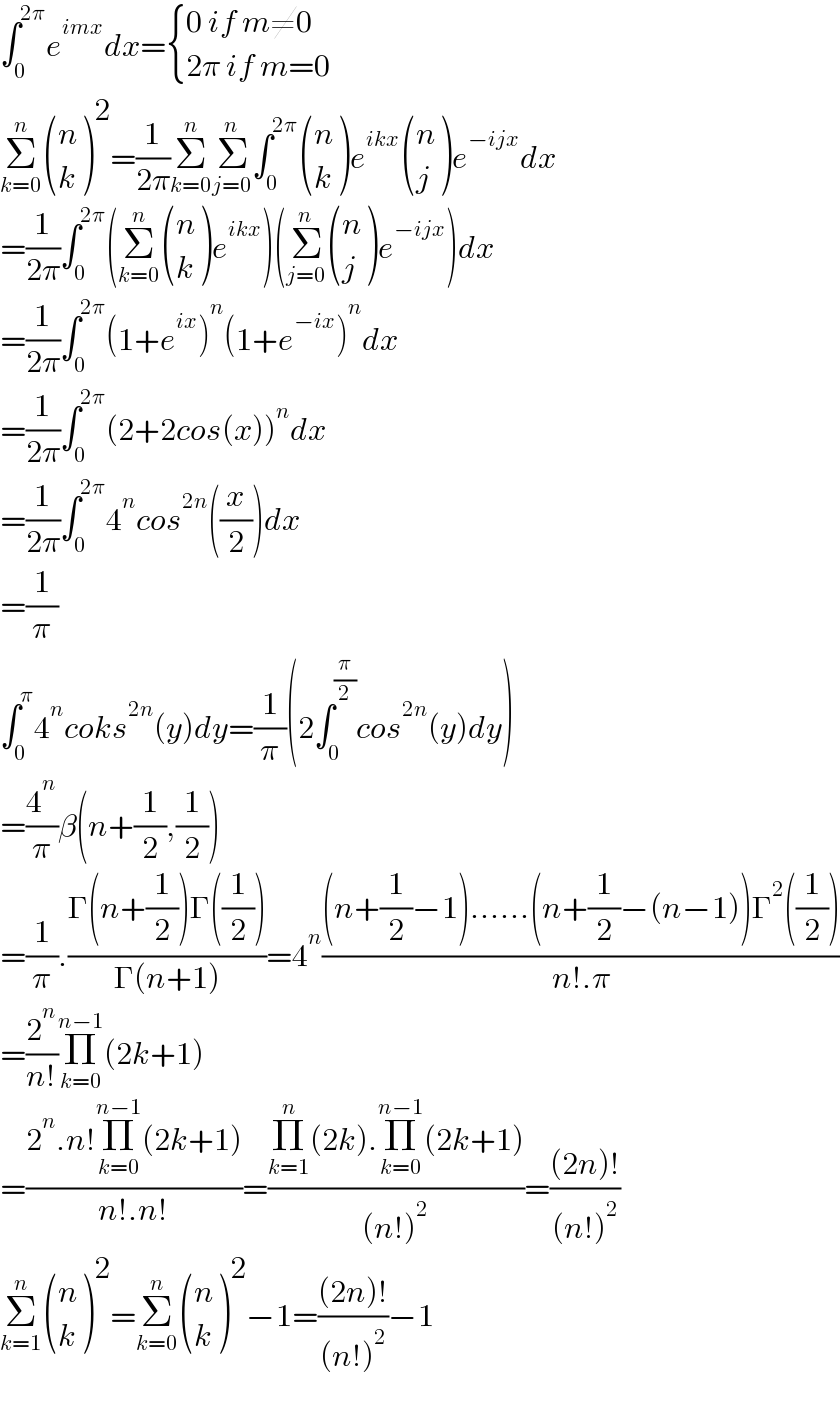
∫_0 ^(2π) e^(imx) dx= { ((0 if m≠0)),((2π if m=0)) :} Σ_(k=0) ^n ((n),(k) )^2 =(1/(2π))Σ_(k=0) ^n Σ_(j=0) ^n ∫_0 ^(2π) ((n),(k) )e^(ikx) ((n),(j) )e^(−ijx) dx =(1/(2π))∫_0 ^(2π) (Σ_(k=0) ^n ((n),(k) )e^(ikx) )(Σ_(j=0) ^n ((n),(j) )e^(−ijx) )dx =(1/(2π))∫_0 ^(2π) (1+e^(ix) )^n (1+e^(−ix) )^n dx =(1/(2π))∫_0 ^(2π) (2+2cos(x))^n dx =(1/(2π))∫_0 ^(2π) 4^n cos^(2n) ((x/2))dx =(1/π) ∫_0 ^π 4^n coks^(2n) (y)dy=(1/π)(2∫_0 ^(π/2) cos^(2n) (y)dy) =(4^n /π)β(n+(1/2),(1/2)) =(1/π).((Γ(n+(1/2))Γ((1/2)))/(Γ(n+1)))=4^n (((n+(1/2)−1)......(n+(1/2)−(n−1))Γ^2 ((1/2)))/(n!.π)) =(2^n /(n!))Π_(k=0) ^(n−1) (2k+1) =((2^n .n!Π_(k=0) ^(n−1) (2k+1))/(n!.n!))=((Π_(k=1) ^n (2k).Π_(k=0) ^(n−1) (2k+1))/((n!)^2 ))=(((2n)!)/((n!)^2 )) Σ_(k=1) ^n ((n),(k) )^2 =Σ_(k=0) ^n ((n),(k) )^2 −1=(((2n)!)/((n!)^2 ))−1

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{{imx}} {dx}=\begin{cases}{\mathrm{0}\:{if}\:{m}\neq\mathrm{0}}\\{\mathrm{2}\pi\:{if}\:{m}=\mathrm{0}}\end{cases} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}\pi}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{e}^{{ikx}} \begin{pmatrix}{{n}}\\{{j}}\end{pmatrix}{e}^{−{ijx}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{e}^{{ikx}} \right)\left(\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{j}}\end{pmatrix}{e}^{−{ijx}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{1}+{e}^{{ix}} \right)^{{n}} \left(\mathrm{1}+{e}^{−{ix}} \right)^{{n}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{2}+\mathrm{2}{cos}\left({x}\right)\right)^{{n}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{4}^{{n}} {cos}^{\mathrm{2}{n}} \left(\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\pi} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{4}^{{n}} {coks}^{\mathrm{2}{n}} \left({y}\right){dy}=\frac{\mathrm{1}}{\pi}\left(\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{n}} \left({y}\right){dy}\right) \\ $$$$=\frac{\mathrm{4}^{{n}} }{\pi}\beta\left({n}+\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\pi}.\frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}+\mathrm{1}\right)}=\mathrm{4}^{{n}} \frac{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)......\left({n}+\frac{\mathrm{1}}{\mathrm{2}}−\left({n}−\mathrm{1}\right)\right)\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}!.\pi} \\ $$$$=\frac{\mathrm{2}^{{n}} }{{n}!}\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}^{{n}} .{n}!\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right)}{{n}!.{n}!}=\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{2}{k}\right).\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right)}{\left({n}!\right)^{\mathrm{2}} }=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} −\mathrm{1}=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}!\right)^{\mathrm{2}} }−\mathrm{1} \\ $$$$ \\ $$

Commented by mr W last updated on 19/Jan/22

great!

$${great}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com