
Question and Answers Forum
Question Number 164547 by mnjuly1970 last updated on 21/Jan/22
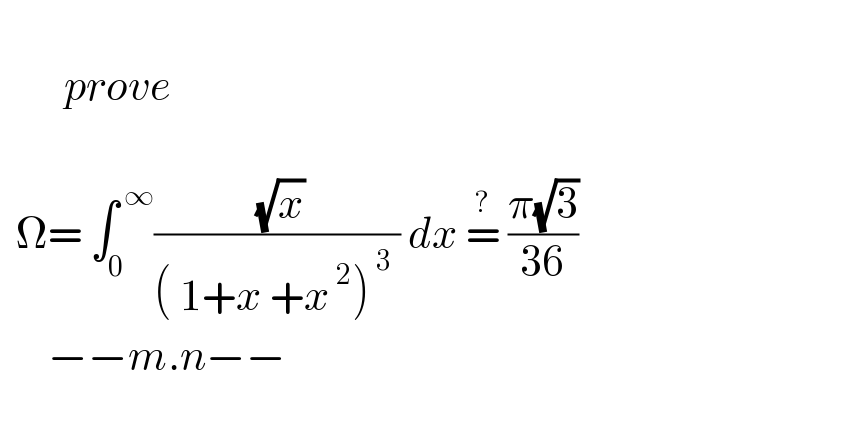
Answered by MJS_new last updated on 19/Jan/22
![∫((√x)/((x^2 +x+2)^3 ))dx= [t=(√x) → dx=2(√x)dt] =2∫(t^2 /((t^4 +t^2 +1)^3 ))dt= [Ostrogradski′s Method] =((t(7t^6 +10t^4 +14t^2 +5))/(12(t^4 +t^2 +1)^2 ))+(1/(12))∫((7t^2 −5)/(t^4 +t^2 +1))dt= (1/(12))∫((7t^2 −5)/(t^4 +t^2 +1))dt= =(1/4)∫((2t−1)/(t^2 −t+1))dt+(1/(24))∫(dt/(t^2 −t+1))−(1/4)∫((2t+1)/(t^2 +t+1))dt+(1/(24))∫(dt/(t^2 +t+1))= ... =(1/4)ln ((t^2 −t+1)/(t^2 +t+1)) +((√3)/(36))(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3)) =((t(7t^6 +10t^4 +14t^2 +5))/(12(t^4 +t^2 +1)^2 ))+(1/4)ln ((t^2 −t+1)/(t^2 +t+1)) +((√3)/(36))(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3))= =(((√x)(7x^3 +10x^2 +14x+5))/(12(x^2 +x+1)^2 ))+(1/4)ln ((x−(√x)+1)/(x+(√x)+1)) +((√3)/(36))(arctan (((√3)(2(√x)−1))/3) +arctan (((√3)(2(√x)+1))/3))+C ⇒ ∫_0 ^∞ ((√x)/((x^2 +x+2)^3 ))dx=(((√3)π)/(36))](Q164566.png)
| ||
Question and Answers Forum | ||
Question Number 164547 by mnjuly1970 last updated on 21/Jan/22 | ||
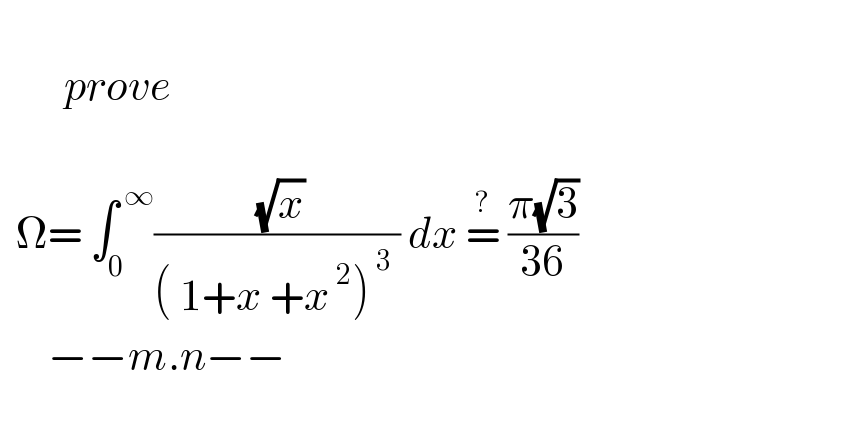 | ||
Answered by MJS_new last updated on 19/Jan/22 | ||
![∫((√x)/((x^2 +x+2)^3 ))dx= [t=(√x) → dx=2(√x)dt] =2∫(t^2 /((t^4 +t^2 +1)^3 ))dt= [Ostrogradski′s Method] =((t(7t^6 +10t^4 +14t^2 +5))/(12(t^4 +t^2 +1)^2 ))+(1/(12))∫((7t^2 −5)/(t^4 +t^2 +1))dt= (1/(12))∫((7t^2 −5)/(t^4 +t^2 +1))dt= =(1/4)∫((2t−1)/(t^2 −t+1))dt+(1/(24))∫(dt/(t^2 −t+1))−(1/4)∫((2t+1)/(t^2 +t+1))dt+(1/(24))∫(dt/(t^2 +t+1))= ... =(1/4)ln ((t^2 −t+1)/(t^2 +t+1)) +((√3)/(36))(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3)) =((t(7t^6 +10t^4 +14t^2 +5))/(12(t^4 +t^2 +1)^2 ))+(1/4)ln ((t^2 −t+1)/(t^2 +t+1)) +((√3)/(36))(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3))= =(((√x)(7x^3 +10x^2 +14x+5))/(12(x^2 +x+1)^2 ))+(1/4)ln ((x−(√x)+1)/(x+(√x)+1)) +((√3)/(36))(arctan (((√3)(2(√x)−1))/3) +arctan (((√3)(2(√x)+1))/3))+C ⇒ ∫_0 ^∞ ((√x)/((x^2 +x+2)^3 ))dx=(((√3)π)/(36))](Q164566.png) | ||
| ||