6 boys and 6 girls go to an exhibition and the cost of ticket is Rs 10.Each girl has a 10 rupees note while each boy has a 20 rupees note. They stand in a queue at the counter and the cashier does not have any money at the begining , then the number of ways of arranging the boys and girls so that no one waits for a change is A) 132 B) 264 C) 132(720)^2 D)264(720)^2


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 164560 by PRITHWISH SEN 2 last updated on 18/Jan/22

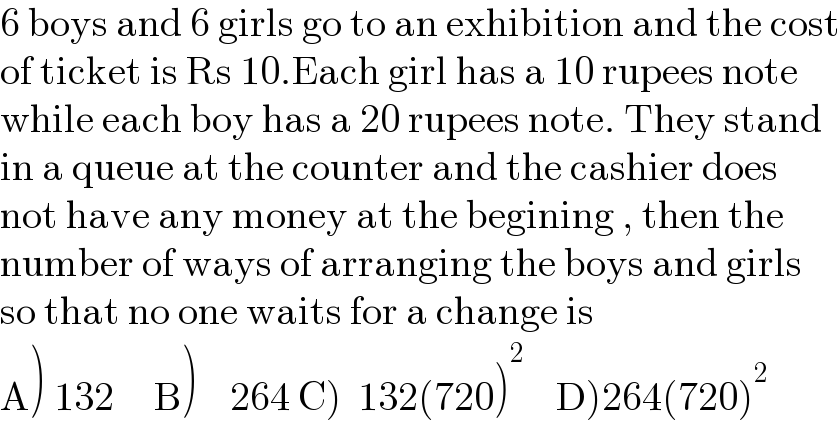
$6 boys and 6 girls go to an exhibition and the cost$ $of ticket is Rs 10 . Each girl has a 10 rupees note$ $while each boy has a 20 rupees note . They stand$ $in a queue at the counter and the cashier does$ $not have any money at the begining, then the$ $number of ways of arranging the boys and girls$ $so that no one waits for a change is$ $A) 132 B) 264 C) 132 {(720)}^{2} D) 264 {(720)}^{2}$
Commented by mr W last updated on 12/Mar/23

$g e n e r a l s o l u t i o n s e e Q 189049$
	Answered by nikif99 last updated on 19/Jan/22

	$C) 132 {(720)}^{2} = 68 428 800$
	Commented by PRITHWISH SEN 2 last updated on 20/Jan/22

	$Thank you sir . But workings ?$
	Commented by nikif99 last updated on 20/Jan/22

	${L e t}^{'} s i g n o r e b o y s . 6 g i r l s c a n s t a n d i n$ $a q u e u e i n 6! w a y s . N o w w e i g n o r e g i r l s .$ $6 b o y s c a n s t a n d i n a q u e u e i n 6! w a y s .$ $M e r g i n g t h e s e q u e u e s i n a n y w a y$ $p r o d u c e s {(6!)}^{2} = 518400 w a y s f o r$ $r e a c h i n g t h e c a s h i e r . N o w t h e p r o b l e m$ $i s ‘ ‘ i n h o w m a n y w a y s c a n w e m e r g e$ $t h e s e t w o l i s t s w i t h t h e r e s t r i c t i o n$ $^{'} n u m b e r o f g i r l s p a s s e d >= n u m b e r$ $o f b o y s {p a s s e d}^{‴} .$ $I s t i l l l o o k f o r t h i s a n s w e r . A l l q u e u e s$ $m u s t s t a r t w i t h g i r l a n d e n d w i t h b o y .$ $U s i n g g r a p h i c d e s i g n I e s t i m a t e t h i s$ $t o 132 . I s u p p o s e n u m b e r o f a c c e p t e d$ $m e r g i n s (132) i s c o m b i n a t i o n s o f 12$ $o v e r 6 (C_{6}^{12}) m i n u s 792 w h i c h r e p r e s e n t$ $q u e u e s n o t f u l l f i l l i n g t h e r e s t r i c t i o n$ $(n e e d t o e x p l o r e h o w t o c o m p u t e i t) .$ $I f s o m e o n e e l s e c o u l d a d v a n c e t o a$ $s o l u t i o n I w o u l d b e h a p p y t o r e a d .$
	Answered by mr W last updated on 24/Jan/22

	$◂ {G B}_{1} {G B}_{2} {G B}_{3} {G B}_{4} {G B}_{5} {G B}_{6}$ $G = p o s i t i o n s o f t h e g i r l s$ $B_{i} = p o s s i b l e p o s i t i o n s o f b o y s$ $a = n u m b e r o f b o y s a t p o s i t i o n B_{1}$ $b = n u m b e r o f b o y s a t p o s i t i o n B_{2}$ $. . .$ $f = n u m b e r o f b o y s a t p o s i t i o n B_{6}$ $a + b + c + d + e + f = 6$ $0 ⩽ a ⩽ 1$ $0 ⩽ b ⩽ 2 - a$ $0 ⩽ c ⩽ 3 - a - b$ $0 ⩽ d ⩽ 4 - a - b - c$ $0 ⩽ e ⩽ 5 - a - b - c - d$ $0 ⩽ f ⩽ 6 - a - b - c - d - e$ $n u m b e r o f w a y s t o p l a c e t h e 6 b o y s$ $i n t o t h e p r o p e r p o s i t i o n s i s$ $n = \underset{a = 0}{\sum^{1}} \underset{b = 0}{\sum^{2 - a}} \underset{c = 0}{\sum^{3 - a - b}} \underset{d = 0}{\sum^{4 - a - b - c}} \underset{e = 0}{\sum^{5 - a - b - c - d}} \underset{f = 0}{\sum^{6 - a - b - c - d - e}} i f (a + b + c + d + e + f = 6)$ $w e g e t n = 132 .$ $i n e a c h o f t h e s e a r r a n g e m e n t s w e$ $h a v e 6! = 720 w a y s t o a r r a n g e t h e b o y s$ $a n d 6! = 720 w a y s t o a r r a n g e t h e g i r l s .$ $s o t h e t o t a l n u m b e r o f w a y s t o$ $q u e u e t h e b o y s a n d g i r l s p r o p e r l y i s$ $132 \times {(720)}^{2} .$
	Commented by mr W last updated on 25/Jan/22

	$h o w t o c a l c u l a t e$ $n = \underset{a = 0}{\sum^{1}} \underset{b = 0}{\sum^{2 - a}} \underset{c = 0}{\sum^{3 - a - b}} \underset{d = 0}{\sum^{4 - a - b - c}} \underset{e = 0}{\sum^{5 - a - b - c - d}} \underset{f = 0}{\sum^{6 - a - b - c - d - e}} i f (a + b + c + d + e + f = 6)$ $w e c a n g e t t h e v a l u e o f n i n f o l l o w i n g$ $w a y, e . g . u s i n g w o l f r a m a l p h a :$ $n_{1} = \underset{a = 0}{\sum^{1}} \underset{b = 0}{\sum^{2 - a}} \underset{c = 0}{\sum^{3 - a - b}} \underset{d = 0}{\sum^{4 - a - b - c}} \underset{e = 0}{\sum^{5 - a - b - c - d}} \underset{f = 0}{\sum^{6 - a - b - c - d - e}} (1)$ $n_{2} = \underset{a = 0}{\sum^{1}} \underset{b = 0}{\sum^{2 - a}} \underset{c = 0}{\sum^{3 - a - b}} \underset{d = 0}{\sum^{4 - a - b - c}} \underset{e = 0}{\sum^{5 - a - b - c - d}} \underset{f = 0}{\sum^{6 - a - b - c - d - e}} ∣ s i g n (a + b + c + d + e + f - 6) ∣$ $n_{1} = 429$ $n_{2} = 297$ $n = n_{1} - n_{2} = 429 - 297 = 132$
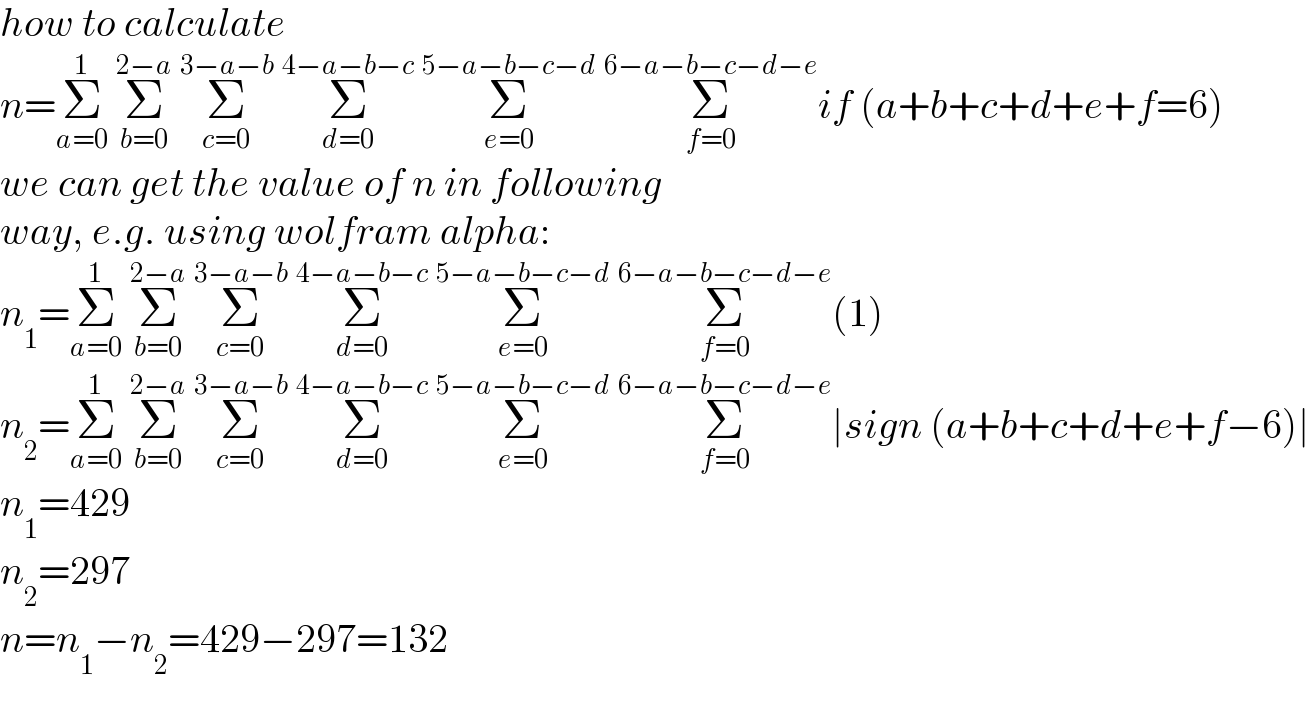
	Commented by mr W last updated on 25/Jan/22

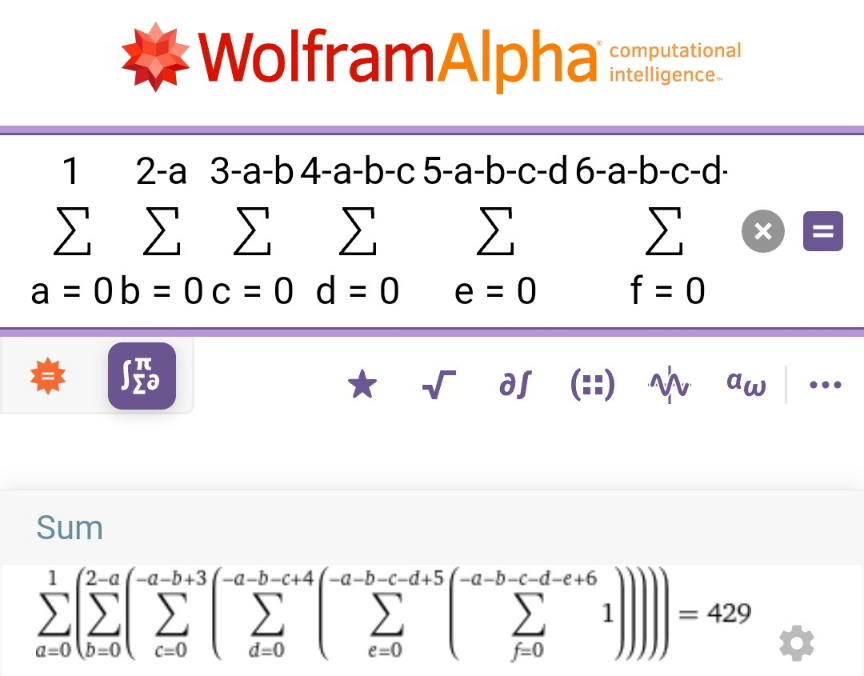
	Commented by mr W last updated on 25/Jan/22

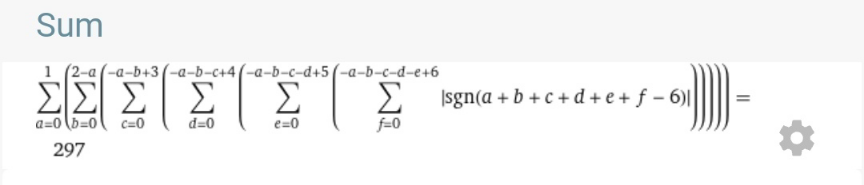
	Commented by nikif99 last updated on 30/Jan/22

	$A w o n d e r f u l l s o l u t i o n t o a c o m p l i c a t e d$ $p r o b l e m . T h a n k y o u S i r W f o r y o u r$ $c o n t r i b u t i o n .$
	Commented by Ar Brandon last updated on 30/Jan/22
	Q161675 , Sir ��
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum