
Question and Answers Forum
Question Number 164653 by mnjuly1970 last updated on 20/Jan/22
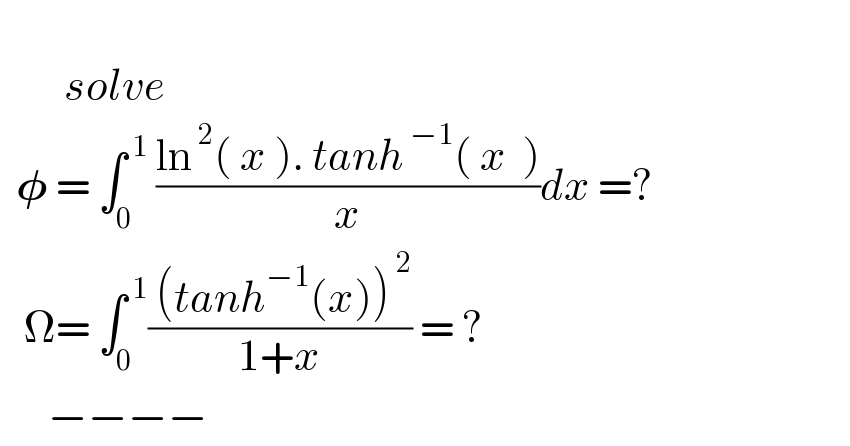
Answered by Lordose last updated on 20/Jan/22
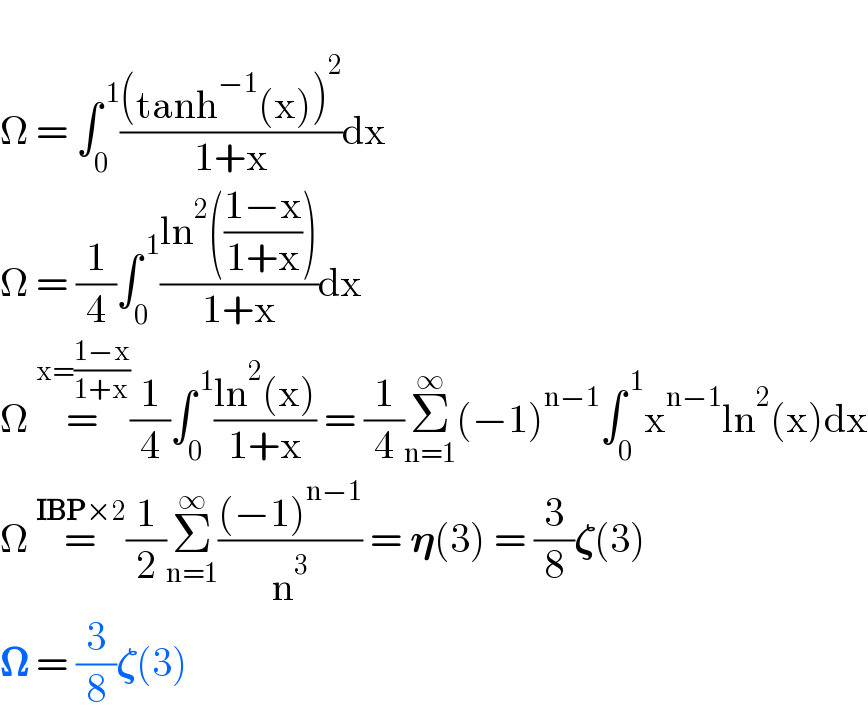
Answered by Ar Brandon last updated on 20/Jan/22
![φ=∫_0 ^1 ((ln^2 xtanh^(−1) (x))/x)dx =[((ln^3 x)/3)tanh^(−1) (x)]_0 ^1 −(1/3)∫_0 ^1 ((ln^3 x)/(1−x^2 ))dx =−(1/3)∙(1/2)∙(1/8)∫_0 ^1 ((u^(−(1/2)) ln^3 u)/(1−u))du=(1/(48))ψ^((3)) ((1/2)) =2(ζ(4)−(1/(16))ζ(4))=((15)/8)ζ(4)=((15)/(720))π^4](Q164666.png)
Commented by mnjuly1970 last updated on 20/Jan/22
| ||
Question and Answers Forum | ||
Question Number 164653 by mnjuly1970 last updated on 20/Jan/22 | ||
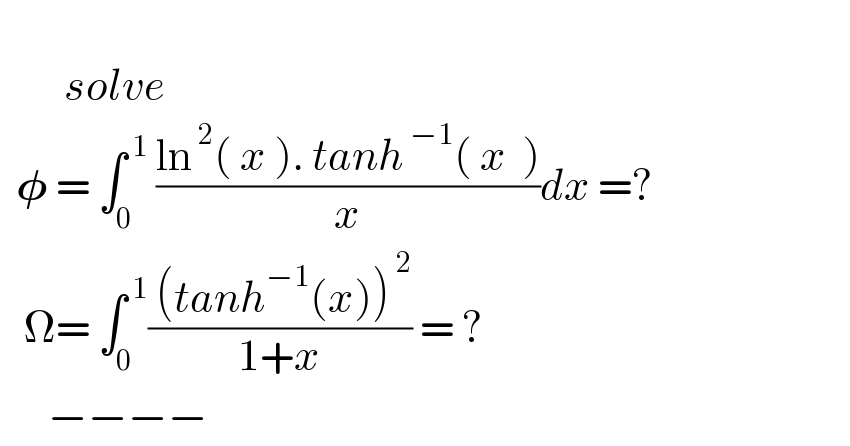 | ||
Answered by Lordose last updated on 20/Jan/22 | ||
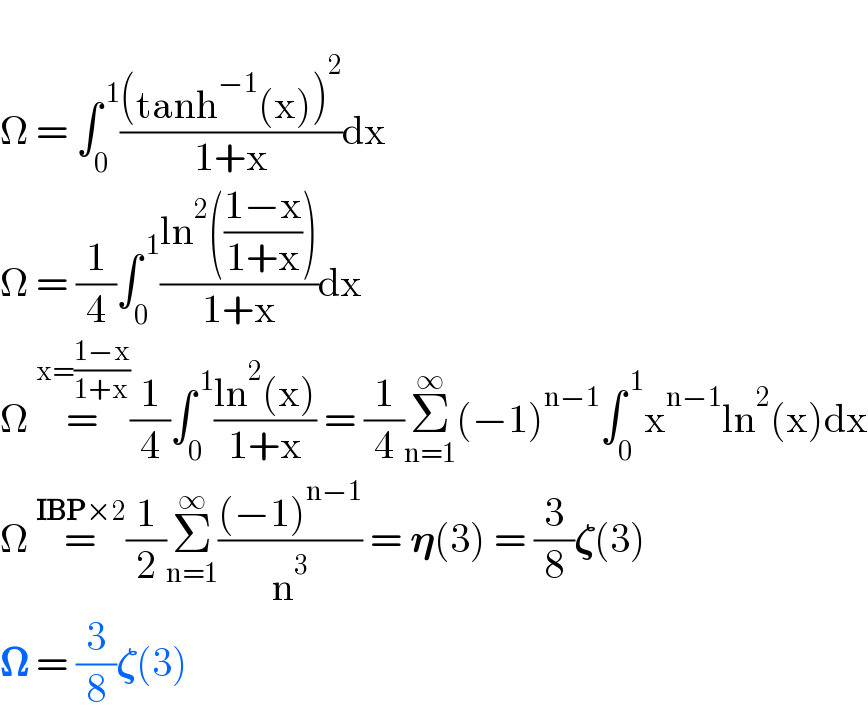 | ||
| ||
Answered by Ar Brandon last updated on 20/Jan/22 | ||
![φ=∫_0 ^1 ((ln^2 xtanh^(−1) (x))/x)dx =[((ln^3 x)/3)tanh^(−1) (x)]_0 ^1 −(1/3)∫_0 ^1 ((ln^3 x)/(1−x^2 ))dx =−(1/3)∙(1/2)∙(1/8)∫_0 ^1 ((u^(−(1/2)) ln^3 u)/(1−u))du=(1/(48))ψ^((3)) ((1/2)) =2(ζ(4)−(1/(16))ζ(4))=((15)/8)ζ(4)=((15)/(720))π^4](Q164666.png) | ||
| ||
Commented by mnjuly1970 last updated on 20/Jan/22 | ||
 | ||