
Question and Answers Forum
Question Number 164705 by Kayela last updated on 20/Jan/22
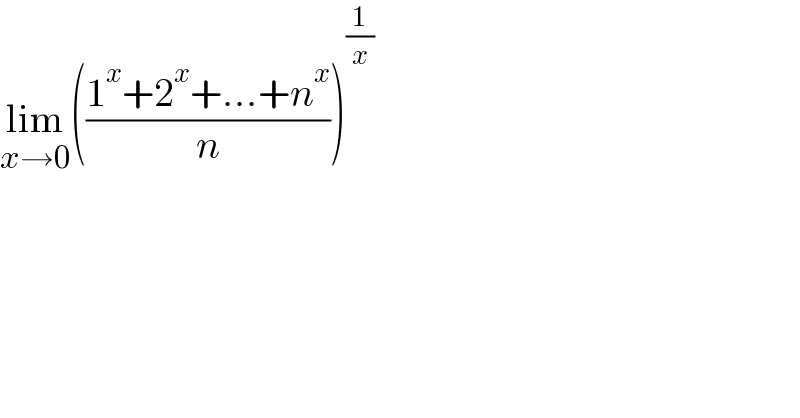
Answered by Berlindo last updated on 20/Jan/22
![=[lim_(x→0) (1+((1^x +2^x +...+n^x −n)/n))^(n/(1^x +2^x +...+n^x −n)) ]^(lim_(x→0) ((1^x +2^x +...+n^x −n)/x)∙(1/n)) =e^(lim_(x→0) (((1^x −1)+(2^x −1)+...+(n^x −1))/x)∙(1/n)) =e^([lim_(x→0) ((1^x −1)/x)+lim_(x→0) ((2^x −1)/x)+...+lim_(x→0) ((n^x −1)/x)]∙(1/n)) =e^((ln 1+ln 2+...+ln n)∙(1/n)) =e^((1/n)ln (n!)) =e^(ln (((n!))^(1/n) )) =((n!))^(1/n) ∴lim_(x→0) (((1^x +2^x +...+n^x )/n))^(1/x) =((n!))^(1/n) ★Berlindo Ndala★](Q164708.png)
Answered by puissant last updated on 21/Jan/22

| ||
Question and Answers Forum | ||
Question Number 164705 by Kayela last updated on 20/Jan/22 | ||
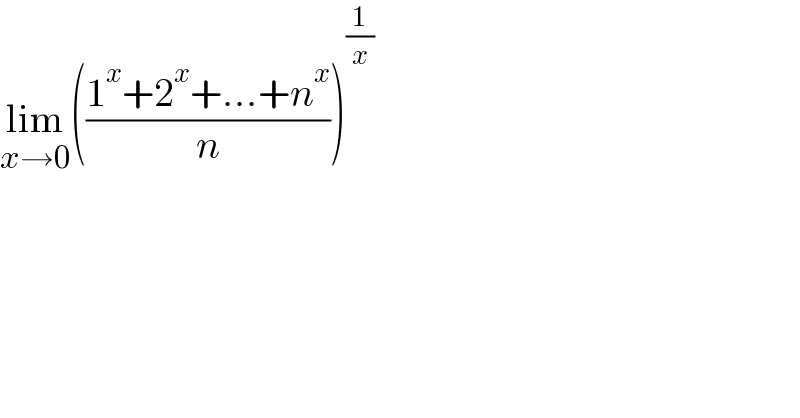 | ||
Answered by Berlindo last updated on 20/Jan/22 | ||
![=[lim_(x→0) (1+((1^x +2^x +...+n^x −n)/n))^(n/(1^x +2^x +...+n^x −n)) ]^(lim_(x→0) ((1^x +2^x +...+n^x −n)/x)∙(1/n)) =e^(lim_(x→0) (((1^x −1)+(2^x −1)+...+(n^x −1))/x)∙(1/n)) =e^([lim_(x→0) ((1^x −1)/x)+lim_(x→0) ((2^x −1)/x)+...+lim_(x→0) ((n^x −1)/x)]∙(1/n)) =e^((ln 1+ln 2+...+ln n)∙(1/n)) =e^((1/n)ln (n!)) =e^(ln (((n!))^(1/n) )) =((n!))^(1/n) ∴lim_(x→0) (((1^x +2^x +...+n^x )/n))^(1/x) =((n!))^(1/n) ★Berlindo Ndala★](Q164708.png) | ||
| ||
Answered by puissant last updated on 21/Jan/22 | ||
 | ||
| ||