Math Question and Answers


Question and Answers Forum

All Questions Topic List
Coordinate Geometry Questions
Previous in All Question Next in All Question
Previous in Coordinate Geometry Next in Coordinate Geometry
Question Number 164728 by mr W last updated on 21/Jan/22

Commented by mr W last updated on 21/Jan/22

$t w o p o i n t s P a n d Q o n t h e p a r a b o l a$ $y = \frac{x^{2}}{a} w i t h ∣ P Q ∣= l . t h e n o r m a l l i n e s$ $a t P a n d Q i n t e r s e c t a t p o i n t S .$ $f i n d t h e l o c u s o f S .$
	Answered by ajfour last updated on 21/Jan/22

	$S (- h, k)$ $N o r m a l f r o m S$ $y = - (\frac{a}{2 p}) x + c P (p, \frac{p^{2}}{a}) l i e s o n i t$ $\frac{p^{2}}{a} = - \frac{a}{2} + c$ ${(p_{2} - p_{1})}^{2} + \frac{{(p_{2}^{2} - p_{1}^{2})}^{2}}{a^{3}} = L^{2} . . . (I)$ $k = \frac{a h}{2 p} + \frac{p^{2}}{a} + \frac{a}{2}$ $\Rightarrow 2 p^{3} + a (a - 2 k) p + a h = 0$ $w e g e t p_{1}, p_{2}, p_{3} i n t e r m s o f$ $h, k, a .$ $s u b s t i t u t i n g i n . . (I) g i v e s r e q u i r e d$ $t h e t h r e e l o c i i, f o r t h r e e c h o i c e s o f$ $p a i r s f r o m a m o n g p_{1}, p_{2}, p_{3} .$
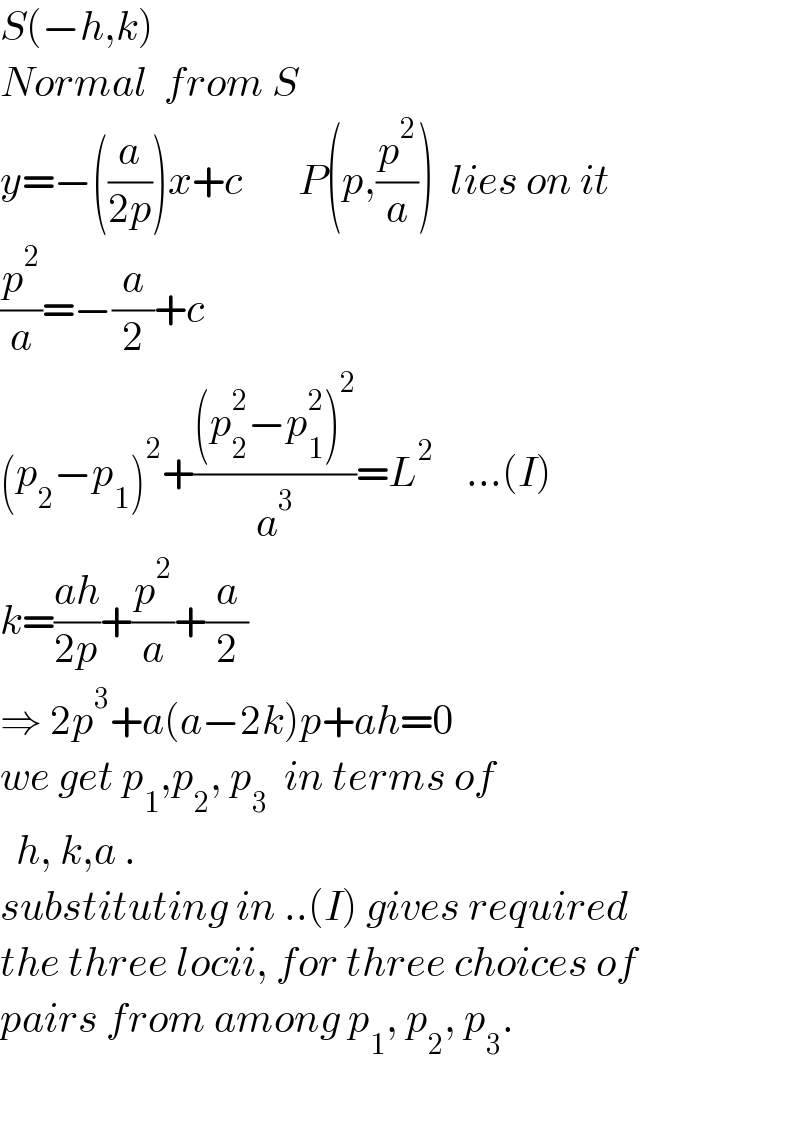
	Commented by mr W last updated on 21/Jan/22

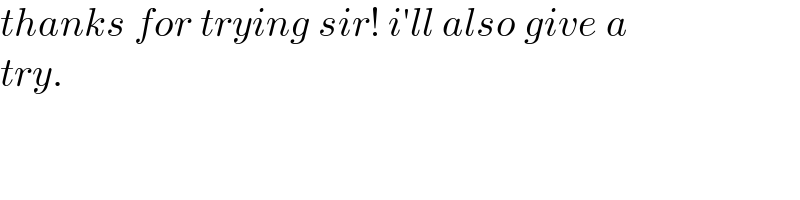
	$t h a n k s f o r t r y i n g s i r! i^{'} l l a l s o g i v e a$ $t r y .$
	Answered by mr W last updated on 21/Jan/22

	Commented by mr W last updated on 23/Jan/22

	$l o c u s i n s h a p e o f a G e r m a n B r e z e l . . .$
	Commented by mr W last updated on 22/Jan/22

	Commented by mr W last updated on 21/Jan/22
	$say P(p, (p^2 /a)), Q(q, (q^2 /a)) tan φ=((2p)/a) tan ϕ=((2q)/a) (q−p)^2 +((q^2 /a)−(p^2 /a))^2 =l^2 (q−p)^2 [1+(((p+q)^2 )/a^2 )]=l^2 [(q+p)^2 −4pq][1+(((p+q)^2 )/a^2 )]=l^2 let u=p+q, v=pq (u^2 −4v)(1+(u^2 /a^2 ))=l^2 ⇒v=(1/4)(u^2 −((a^2 l^2 )/(a^2 +u^2 ))) eqn. of PS: y=(p^2 /a)−(a/(2p))(x−p) y=(p^2 /a)+(a/2)−((ax)/(2p)) eqn. of QS: y=(q^2 /a)+(a/2)−((ax)/(2q)) say intersection point S(x_s ,y_s ) (p^2 /a)+(a/2)−((ax_s )/(2p))=(q^2 /a)+(a/2)−((ax_s )/(2q)) (p^2 /a)−((ax_s )/(2p))=(q^2 /a)−((ax_s )/(2q)) x_s =−((2(q+p)pq)/a^2 ) ⇒x_s =−((2uv)/a^2 ) 2y_s =((p^2 +q^2 )/a)+a−ax_s ((1/(2p))+(1/(2q))) y_s =(a/2)+((p^2 +q^2 )/(2a))−((a(p+q)x_s )/(4pq)) y_s =(a/2)+(((p+q)^2 −pq)/a) ⇒y_s =(a/2)+((u^2 −v)/a) taking u as parameter we get the eqn. of locus of point S: { ((x=−((2uv)/a^2 ))),((y=(a/2)+((u^2 −v)/a))) :} with v=(1/4)(u^2 −((a^2 l^2 )/(a^2 +u^2 ))) with u given, p, q are roots of z^2 −uz+(1/4)(u^2 −((a^2 l^2 )/(a^2 +u^2 )))=0 ⇒p,q=(1/2)(u∓((al)/( (√(a^2 +u^2 )))))$
	$s a y P (p, \frac{p^{2}}{a}), Q (q, \frac{q^{2}}{a})$ $\tan ϕ = \frac{2 p}{a}$ $\tan φ = \frac{2 q}{a}$ ${(q - p)}^{2} + {(\frac{q^{2}}{a} - \frac{p^{2}}{a})}^{2} = l^{2}$ ${(q - p)}^{2} [1 + \frac{{(p + q)}^{2}}{a^{2}}] = l^{2}$ $[{(q + p)}^{2} - 4 p q] [1 + \frac{{(p + q)}^{2}}{a^{2}}] = l^{2}$ $l e t u = p + q, v = p q$ $(u^{2} - 4 v) (1 + \frac{u^{2}}{a^{2}}) = l^{2}$ $\Rightarrow v = \frac{1}{4} (u^{2} - \frac{a^{2} l^{2}}{a^{2} + u^{2}})$ $e q n . o f P S :$ $y = \frac{p^{2}}{a} - \frac{a}{2 p} (x - p)$ $y = \frac{p^{2}}{a} + \frac{a}{2} - \frac{a x}{2 p}$ $e q n . o f Q S :$ $y = \frac{q^{2}}{a} + \frac{a}{2} - \frac{a x}{2 q}$ $s a y i n t e r s e c t i o n p o i n t S (x_{s}, y_{s})$ $\frac{p^{2}}{a} + \frac{a}{2} - \frac{{a x}_{s}}{2 p} = \frac{q^{2}}{a} + \frac{a}{2} - \frac{{a x}_{s}}{2 q}$ $\frac{p^{2}}{a} - \frac{{a x}_{s}}{2 p} = \frac{q^{2}}{a} - \frac{{a x}_{s}}{2 q}$ $x_{s} = - \frac{2 (q + p) p q}{a^{2}}$ $\Rightarrow x_{s} = - \frac{2 u v}{a^{2}}$ $2 y_{s} = \frac{p^{2} + q^{2}}{a} + a - {a x}_{s} (\frac{1}{2 p} + \frac{1}{2 q})$ $y_{s} = \frac{a}{2} + \frac{p^{2} + q^{2}}{2 a} - \frac{a (p + q) x_{s}}{4 p q}$ $y_{s} = \frac{a}{2} + \frac{{(p + q)}^{2} - p q}{a}$ $\Rightarrow y_{s} = \frac{a}{2} + \frac{u^{2} - v}{a}$ $t a k i n g u a s p a r a m e t e r w e g e t t h e e q n .$ $o f l o c u s o f p o i n t S :$ ${\begin{cases} x = - \frac{2 u v}{a^{2}} \\ y = \frac{a}{2} + \frac{u^{2} - v}{a} \end{cases} w i t h v = \frac{1}{4} (u^{2} - \frac{a^{2} l^{2}}{a^{2} + u^{2}})$ $w i t h u g i v e n, p, q a r e r o o t s o f$ $z^{2} - u z + \frac{1}{4} (u^{2} - \frac{a^{2} l^{2}}{a^{2} + u^{2}}) = 0$ $\Rightarrow p, q = \frac{1}{2} (u \mp \frac{a l}{\sqrt{a^{2} + u^{2}}})$
	Commented by mr W last updated on 21/Jan/22

	Commented by mr W last updated on 21/Jan/22

	Commented by ajfour last updated on 21/Jan/22

	$g r e a t w o r k i n g s s i r, i w i l l t r y n$ $f o l l o w . .$
	Commented by Tawa11 last updated on 21/Jan/22

	$Weldone sir$
	Answered by ajfour last updated on 23/Jan/22
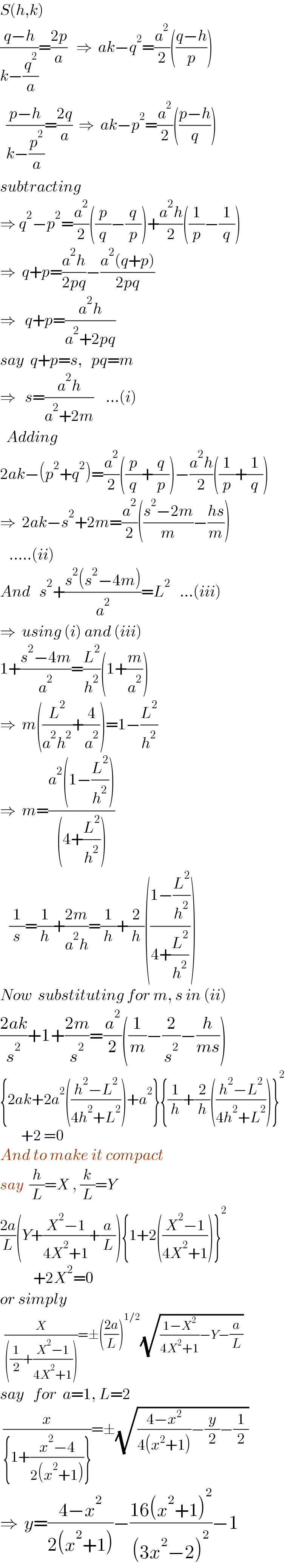
	$S(h,k) ((q−h)/(k−(q^2 /a)))=((2p)/a) ⇒ ak−q^2 =(a^2 /2)(((q−h)/p)) ((p−h)/(k−(p^2 /a)))=((2q)/a) ⇒ ak−p^2 =(a^2 /2)(((p−h)/q)) subtracting ⇒ q^2 −p^2 =(a^2 /2)((p/q)−(q/p))+((a^2 h)/2)((1/p)−(1/q)) ⇒ q+p=((a^2 h)/(2pq))−((a^2 (q+p))/(2pq)) ⇒ q+p=((a^2 h)/(a^2 +2pq)) say q+p=s, pq=m ⇒ s=((a^2 h)/(a^2 +2m)) ...(i) Adding 2ak−(p^2 +q^2 )=(a^2 /2)((p/q)+(q/p))−((a^2 h)/2)((1/p)+(1/q)) ⇒ 2ak−s^2 +2m=(a^2 /2)(((s^2 −2m)/m)−((hs)/m)) .....(ii) And s^2 +((s^2 (s^2 −4m))/a^2 )=L^2 ...(iii) ⇒ using (i) and (iii) 1+((s^2 −4m)/a^2 )=(L^2 /h^2 )(1+(m/a^2 )) ⇒ m((L^2 /(a^2 h^2 ))+(4/a^2 ))=1−(L^2 /h^2 ) ⇒ m=((a^2 (1−(L^2 /h^2 )))/((4+(L^2 /h^2 )))) (1/s)=(1/h)+((2m)/(a^2 h))=(1/h)+(2/h)(((1−(L^2 /h^2 ))/(4+(L^2 /h^2 )))) Now substituting for m, s in (ii) ((2ak)/s^2 )+1+((2m)/s^2 )=(a^2 /2)((1/m)−(2/s^2 )−(h/(ms))) {2ak+2a^2 (((h^2 −L^2 )/(4h^2 +L^2 )))+a^2 }{(1/h)+(2/h)(((h^2 −L^2 )/(4h^2 +L^2 )))}^2 +2 =0 And to make it compact say (h/L)=X , (k/L)=Y ((2a)/L)(Y+((X^2 −1)/(4X^2 +1))+(a/L)){1+2(((X^2 −1)/(4X^2 +1)))}^2 +2X^2 =0 or simply (X/(((1/2)+((X^2 −1)/(4X^2 +1)))))=±(((2a)/L))^(1/2) (√(((1−X^2 )/(4X^2 +1))−Y−(a/L))) say for a=1, L=2 (x/({1+((x^2 −4)/(2(x^2 +1)))}))=±(√(((4−x^2 )/(4(x^2 +1)))−(y/2)−(1/2))) ⇒ y=((4−x^2 )/(2(x^2 +1)))−((16(x^2 +1)^2 )/((3x^2 −2)^2 ))−1$
	$S (h, k)$ $\frac{q - h}{k - \frac{q^{2}}{a}} = \frac{2 p}{a} \Rightarrow a k - q^{2} = \frac{a^{2}}{2} (\frac{q - h}{p})$ $\frac{p - h}{k - \frac{p^{2}}{a}} = \frac{2 q}{a} \Rightarrow a k - p^{2} = \frac{a^{2}}{2} (\frac{p - h}{q})$ $s u b t r a c t i n g$ $\Rightarrow q^{2} - p^{2} = \frac{a^{2}}{2} (\frac{p}{q} - \frac{q}{p}) + \frac{a^{2} h}{2} (\frac{1}{p} - \frac{1}{q})$ $\Rightarrow q + p = \frac{a^{2} h}{2 p q} - \frac{a^{2} (q + p)}{2 p q}$ $\Rightarrow q + p = \frac{a^{2} h}{a^{2} + 2 p q}$ $s a y q + p = s, p q = m$ $\Rightarrow s = \frac{a^{2} h}{a^{2} + 2 m} . . . (i)$ $A d d i n g$ $2 a k - (p^{2} + q^{2}) = \frac{a^{2}}{2} (\frac{p}{q} + \frac{q}{p}) - \frac{a^{2} h}{2} (\frac{1}{p} + \frac{1}{q})$ $\Rightarrow 2 a k - s^{2} + 2 m = \frac{a^{2}}{2} (\frac{s^{2} - 2 m}{m} - \frac{h s}{m})$ $. . . . . (i i)$ $A n d s^{2} + \frac{s^{2} (s^{2} - 4 m)}{a^{2}} = L^{2} . . . (i i i)$ $\Rightarrow u s i n g (i) a n d (i i i)$ $1 + \frac{s^{2} - 4 m}{a^{2}} = \frac{L^{2}}{h^{2}} (1 + \frac{m}{a^{2}})$ $\Rightarrow m (\frac{L^{2}}{a^{2} h^{2}} + \frac{4}{a^{2}}) = 1 - \frac{L^{2}}{h^{2}}$ $\Rightarrow m = \frac{a^{2} (1 - \frac{L^{2}}{h^{2}})}{(4 + \frac{L^{2}}{h^{2}})}$ $\frac{1}{s} = \frac{1}{h} + \frac{2 m}{a^{2} h} = \frac{1}{h} + \frac{2}{h} (\frac{1 - \frac{L^{2}}{h^{2}}}{4 + \frac{L^{2}}{h^{2}}})$ $N o w s u b s t i t u t i n g f o r m, s i n (i i)$ $\frac{2 a k}{s^{2}} + 1 + \frac{2 m}{s^{2}} = \frac{a^{2}}{2} (\frac{1}{m} - \frac{2}{s^{2}} - \frac{h}{m s})$ ${2 a k + 2 a^{2} (\frac{h^{2} - L^{2}}{4 h^{2} + L^{2}}) + a^{2}} {\frac{1}{h} + \frac{2}{h} (\frac{h^{2} - L^{2}}{4 h^{2} + L^{2}})}^{2}$ $+ 2 = 0$ $A n d t o m a k e i t c o m p a c t$ $s a y \frac{h}{L} = X, \frac{k}{L} = Y$ $\frac{2 a}{L} (Y + \frac{X^{2} - 1}{4 X^{2} + 1} + \frac{a}{L}) {1 + 2 (\frac{X^{2} - 1}{4 X^{2} + 1})}^{2}$ $+ 2 X^{2} = 0$ $o r s i m p l y$ $\frac{X}{(\frac{1}{2} + \frac{X^{2} - 1}{4 X^{2} + 1})} = \pm {(\frac{2 a}{L})}^{1 / 2} \sqrt{\frac{1 - X^{2}}{4 X^{2} + 1} - Y - \frac{a}{L}}$ $s a y f o r a = 1, L = 2$ $\frac{x}{{1 + \frac{x^{2} - 4}{2 (x^{2} + 1)}}} = \pm \sqrt{\frac{4 - x^{2}}{4 (x^{2} + 1)} - \frac{y}{2} - \frac{1}{2}}$ $\Rightarrow y = \frac{4 - x^{2}}{2 (x^{2} + 1)} - \frac{16 {(x^{2} + 1)}^{2}}{{(3 x^{2} - 2)}^{2}} - 1$
	Commented by ajfour last updated on 23/Jan/22

	$s o m e l i t t l e e r r o r . . . i s h a l l e d i t$ $t o d a y . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum