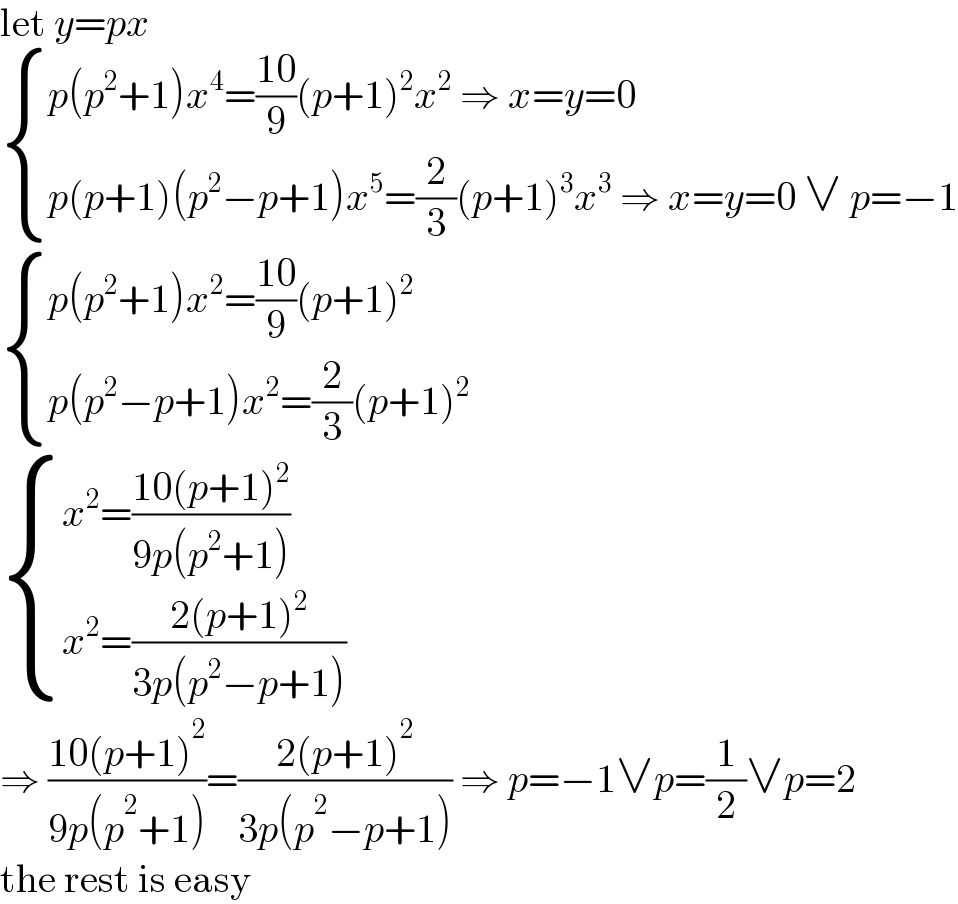Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 164787 by cortano1 last updated on 22/Jan/22

Answered by mr W last updated on 22/Jan/22

xy[(x+y)^2 −2xy]=((10(x+y)^2 )/9) xy[(x+y)^3 −3xy(x+y)]=((2(x+y)^3 )/3) let u=x+y, v=xy { ((v(u^2 −2v)=((10u^2 )/9) ...(i))),((vu(u^2 −3v)=((2u^3 )/3) ...(ii))) :} from (ii): u=0 ⇒v=0 ⇒x=y=0 or u≠0 ⇒v≠0 v(u^2 −3v)=((2u^2 )/3) ...(iii) (i)/(ii): ((u^2 −2v)/(u^2 −3v))=(5/3) 2u^2 =9v ⇒v=((2u^2 )/9) put this into (iii): ((2u^2 )/9)(u^2 −3×((2u^2 )/9))=((2u^2 )/3) u^2 =9 ⇒u=±3 ⇒v=2 x,y are roots of z^2 −uz+v=0 x,y=((u±(√(u^2 −4v)))/2)=((±3±1)/2)=2, 1 or −2,−1 summary: (x,y)=(0,0), (−2,−1),(−1,−2),(2,1),(1,2)

$${xy}\left[\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}\right]=\frac{\mathrm{10}\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{9}} \\ $$$${xy}\left[\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right)\right]=\frac{\mathrm{2}\left({x}+{y}\right)^{\mathrm{3}} }{\mathrm{3}} \\ $$$${let}\:{u}={x}+{y},\:{v}={xy} \\ $$$$\begin{cases}{{v}\left({u}^{\mathrm{2}} −\mathrm{2}{v}\right)=\frac{\mathrm{10}{u}^{\mathrm{2}} }{\mathrm{9}}\:\:\:...\left({i}\right)}\\{{vu}\left({u}^{\mathrm{2}} −\mathrm{3}{v}\right)=\frac{\mathrm{2}{u}^{\mathrm{3}} }{\mathrm{3}}\:\:\:...\left({ii}\right)}\end{cases} \\ $$$${from}\:\left({ii}\right): \\ $$$${u}=\mathrm{0} \\ $$$$\Rightarrow{v}=\mathrm{0} \\ $$$$\Rightarrow{x}={y}=\mathrm{0} \\ $$$${or} \\ $$$${u}\neq\mathrm{0}\:\Rightarrow{v}\neq\mathrm{0} \\ $$$${v}\left({u}^{\mathrm{2}} −\mathrm{3}{v}\right)=\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{3}}\:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\frac{{u}^{\mathrm{2}} −\mathrm{2}{v}}{{u}^{\mathrm{2}} −\mathrm{3}{v}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{2}{u}^{\mathrm{2}} =\mathrm{9}{v} \\ $$$$\Rightarrow{v}=\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${put}\:{this}\:{into}\:\left({iii}\right): \\ $$$$\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{9}}\left({u}^{\mathrm{2}} −\mathrm{3}×\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{9}}\right)=\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${u}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow{u}=\pm\mathrm{3} \\ $$$$\Rightarrow{v}=\mathrm{2} \\ $$$${x},{y}\:{are}\:{roots}\:{of}\:{z}^{\mathrm{2}} −{uz}+{v}=\mathrm{0} \\ $$$${x},{y}=\frac{{u}\pm\sqrt{{u}^{\mathrm{2}} −\mathrm{4}{v}}}{\mathrm{2}}=\frac{\pm\mathrm{3}\pm\mathrm{1}}{\mathrm{2}}=\mathrm{2},\:\mathrm{1}\:{or}\:−\mathrm{2},−\mathrm{1} \\ $$$${summary}: \\ $$$$\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right),\:\left(−\mathrm{2},−\mathrm{1}\right),\left(−\mathrm{1},−\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{1},\mathrm{2}\right) \\ $$

Commented by leonhard77 last updated on 22/Jan/22

(i):(ii)⇒(5/(3u))

$$\left({i}\right):\left({ii}\right)\Rightarrow\frac{\mathrm{5}}{\mathrm{3}{u}} \\ $$

Commented by mr W last updated on 22/Jan/22

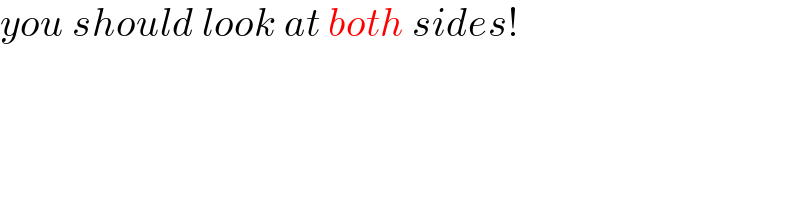
you should look at both sides!

$${you}\:{should}\:{look}\:{at}\:{both}\:{sides}! \\ $$

Commented by cortano1 last updated on 22/Jan/22

Commented by Tawa11 last updated on 22/Jan/22

Great sirs

$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Answered by MJS_new last updated on 22/Jan/22

let y=px { ((p(p^2 +1)x^4 =((10)/9)(p+1)^2 x^2 ⇒ x=y=0)),((p(p+1)(p^2 −p+1)x^5 =(2/3)(p+1)^3 x^3 ⇒ x=y=0 ∨ p=−1)) :} { ((p(p^2 +1)x^2 =((10)/9)(p+1)^2 )),((p(p^2 −p+1)x^2 =(2/3)(p+1)^2 )) :} { ((x^2 =((10(p+1)^2 )/(9p(p^2 +1))))),((x^2 =((2(p+1)^2 )/(3p(p^2 −p+1))))) :} ⇒ ((10(p+1)^2 )/(9p(p^2 +1)))=((2(p+1)^2 )/(3p(p^2 −p+1))) ⇒ p=−1∨p=(1/2)∨p=2 the rest is easy

$$\mathrm{let}\:{y}={px} \\ $$$$\begin{cases}{{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{4}} =\frac{\mathrm{10}}{\mathrm{9}}\left({p}+\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}} \:\Rightarrow\:{x}={y}=\mathrm{0}}\\{{p}\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right){x}^{\mathrm{5}} =\frac{\mathrm{2}}{\mathrm{3}}\left({p}+\mathrm{1}\right)^{\mathrm{3}} {x}^{\mathrm{3}} \:\Rightarrow\:{x}={y}=\mathrm{0}\:\vee\:{p}=−\mathrm{1}}\end{cases} \\ $$$$\begin{cases}{{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{2}} =\frac{\mathrm{10}}{\mathrm{9}}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }\\{{p}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right){x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }\end{cases} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} =\frac{\mathrm{10}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}}\\{{x}^{\mathrm{2}} =\frac{\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}{p}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)}}\end{cases} \\ $$$$\Rightarrow\:\frac{\mathrm{10}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}{p}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)}\:\Rightarrow\:{p}=−\mathrm{1}\vee{p}=\frac{\mathrm{1}}{\mathrm{2}}\vee{p}=\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com