Question and Answers Forum
Question Number 164842 by ajfour last updated on 22/Jan/22

Commented by MJS_new last updated on 22/Jan/22
Commented by ajfour last updated on 22/Jan/22
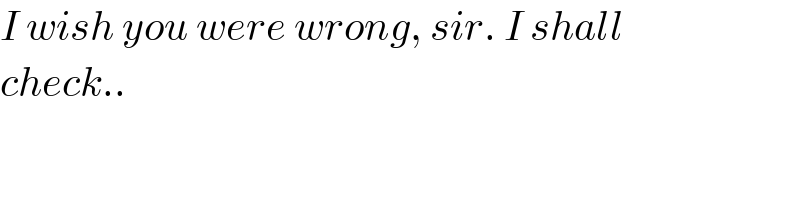
Commented by mr W last updated on 22/Jan/22
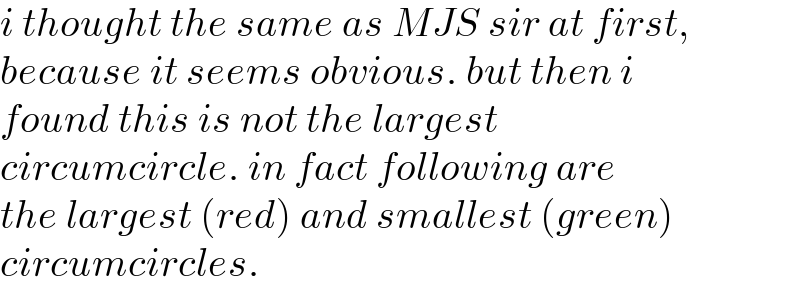
Commented by mr W last updated on 22/Jan/22

Commented by mr W last updated on 22/Jan/22
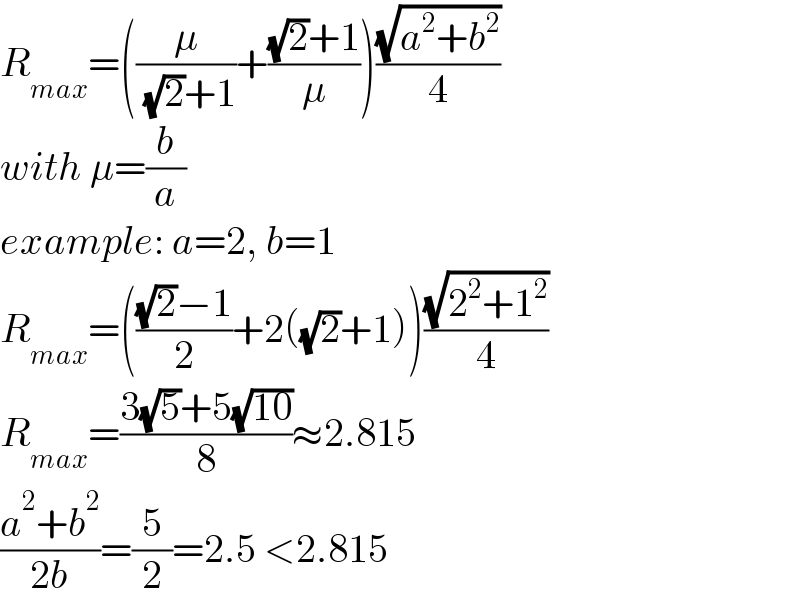
Commented by MJS_new last updated on 23/Jan/22

Commented by MJS_new last updated on 23/Jan/22

Commented by MJS_new last updated on 23/Jan/22
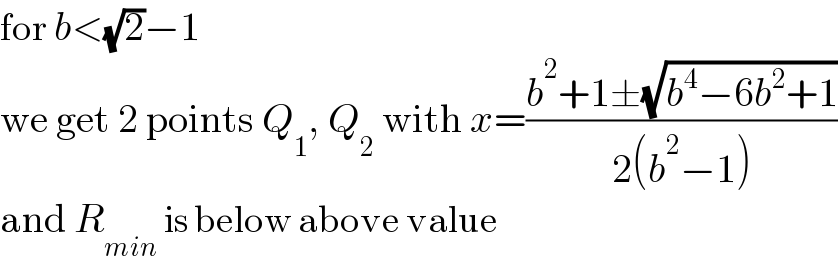
Commented by MJS_new last updated on 23/Jan/22
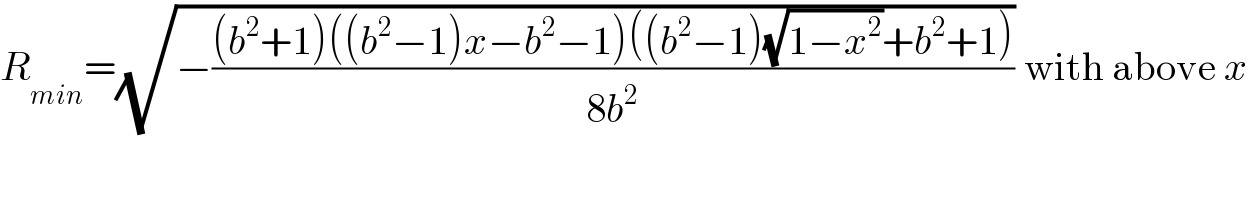
Commented by mr W last updated on 23/Jan/22

Commented by mr W last updated on 23/Jan/22

Commented by mr W last updated on 23/Jan/22

Commented by mr W last updated on 23/Jan/22
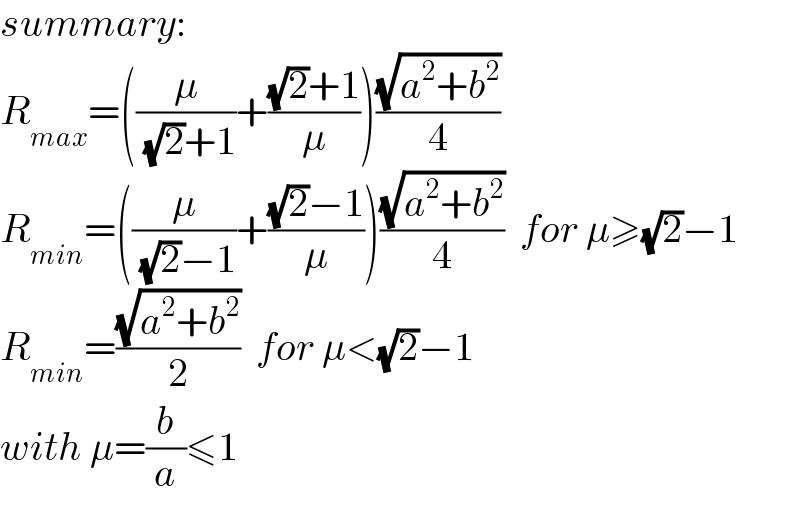
Answered by ajfour last updated on 22/Jan/22
![P(acos θ,bsin θ) condider line y−((asin θ)/2)=−(((acos θ+a)/(asin θ)))(x−((a−acos θ)/2)) And line y+(b/2)=(a/b)(x+(a/2)) subteacting (b/2)+((asin θ)/2)=((a/b)+((1+cos θ)/(sin θ)))x +(a^2 /(2b))−((asin θ)/2) ⇒ x=((((a^2 +b^2 )/b)+asin θ)/(2((a/b)+((1+cos θ)/(sin θ))))) y+b=((a^2 +b^2 )/(2b))+(a/b){((((a^2 +b^2 )/b)+asin θ)/(2((a/b)+((1+cos θ)/(sin θ)))))} x^2 +(y+b)^2 =R^2 R^2 ={((((a^2 +b^2 )/b)+asin θ)/(2((a/b)+((1+cos θ)/(sin θ)))))}^2 + +[((a^2 +b^2 )/(2b))+(a/b){((((a^2 +b^2 )/b)+asin θ)/(2((a/b)+((1+cos θ)/(sin θ)))))}]^2 R^2 =(((((a^2 +b^2 )/b)+asin θ)^2 +[4(((a^2 +b^2 )/(2b)))((a/b)+((1+cos θ)/(sin θ)))^2 +(a/b)(((a^2 +b^2 )/b)+asin θ)^2 ]^2 )/(4((a/b)+((1+cos θ)/(sin θ)))^2 )) let for example a=2, b=1 R^2 =(((5+2sin θ)^2 +[10(2+((1+cos θ)/(sin θ)))^2 +2(5+2sin θ)^2 ]^2 )/(4(2+((1+cos θ)/(sin θ)))^2 )) .....](Q164869.png)
Commented by Tawa11 last updated on 22/Jan/22

Answered by ajfour last updated on 23/Jan/22
![Let left end be origin O. slope p=((bsin θ)/(a+acos θ)) p^2 +1=((a^2 (1+cos θ)^2 +b^2 sin^2 θ)/(a^2 (1+cos θ)^2 )) slope q=((b+bsin θ)/(acos θ)) tan φ=tan (tan^(−1) q−tan^(−1) p) R is maximum if φ=φ_(max) . tan φ=((q−p)/(1+pq)) ((d(tan φ))/dθ)=0 ⇒ (((1+pq)((dq/dθ)−(dp/dθ))−(q−p)[q((dp/dθ))+p((dq/dθ))])/((1+pq)^2 )) =0 (1+p^2 )((dq/dθ))=(1+q^2 )((dp/dθ)) (1+p^2 )[((abcos^2 θ+asin θ(b+bsin θ))/(a^2 cos^2 θ))] =(1+q^2 )[(((1+q^2 )[abcos θ(1+cos θ)+absin^2 θ])/((a+acos θ)^2 )) ⇒ (1+p^2 )(((1+sin θ)/(cos^2 θ)))=(1+q^2 )((1/(1+cos θ))) ....](Q164897.png)
Answered by mr W last updated on 23/Jan/22

Commented by mr W last updated on 24/Jan/22
![let μ=(b/a)≤1 A(−a,0) B(0,−b) say P(a cos θ, b sin θ) AP=(√(a^2 (1+cos θ)^2 +b^2 sin^2 θ)) ⇒AP=a(√((1+cos θ)^2 +μ^2 sin^2 θ)) BP=(√(a^2 cos^2 θ+b^2 (1+sin θ)^2 )) ⇒BP=a(√(cos^2 θ+μ^2 (1+sin θ)^2 )) AB=(√(a^2 +b^2 ))=a(√(1+μ^2 )) eqn. of AB: (x/a)+(y/b)+1=0 distance from P to AB: d=((∣cos θ+sin θ+1∣)/( (√((1/a^2 )+(1/b^2 )))))=((a^2 μ∣cos θ+sin θ+1∣)/( (√(a^2 +b^2 )))) area of ΔABP: Δ=(d(√(a^2 +b^2 ))/2)=((a^2 μ(cos θ+sin θ+1))/2) Δ=((AP×BP sin φ)/2) Δ=((a^2 sin φ(√([(1+cos θ)^2 +μ^2 sin^2 θ][cos^2 θ+μ^2 (1+sin θ)^2 ])))/2) ((a^2 μ(cos θ+sin θ+1))/2)=((a^2 sin φ(√([(1+cos θ)^2 +μ^2 sin^2 θ][cos^2 θ+μ^2 (1+sin θ)^2 ])))/2) sin φ=((μ(cos θ+sin θ+1))/( (√([(1+cos θ)^2 +μ^2 sin^2 θ][cos^2 θ+μ^2 (1+sin θ)^2 ])))) R=radius of circumcircle of ΔABP AB=2R sin φ R=((AB)/(2 sin φ)) R=((√(a^2 +b^2 ))/(2μ))×((√([(1+cos θ)^2 +μ^2 sin^2 θ][cos^2 θ+μ^2 (1+sin θ)^2 ]))/(cos θ+sin θ+1)) R=(((1−μ^2 )(√(a^2 +b^2 )))/(2μ))×((√((1+cos θ)(1+sin θ)(((1+μ^2 )/(1−μ^2 ))+cos θ)(((1+μ^2 )/(1−μ^2 ))−sin θ)))/(cos θ+sin θ+1)) let λ=((1+μ^2 )/(1−μ^2 )) R=(((1−μ^2 )(√(a^2 +b^2 )))/(2μ))×((√((1+cos θ)(1+sin θ)(λ+cos θ)(λ−sin θ)))/(cos θ+sin θ+1)) R=(((1−μ^2 )(√(a^2 +b^2 )))/(2μ))×(√(Φ(θ))) Φ(θ)=(((1+cos θ)(1+sin θ)(λ+cos θ)(λ−sin θ))/((cos θ+sin θ+1)^2 )) ln Φ(θ)=ln (1+cos θ)+ln (1+sin θ)+ln (λ+cos θ)+ln (λ−sin θ)−2 ln (cos θ+sin θ+1) ((Φ′(θ))/(Φ(θ)))=((−sin θ)/(1+cos θ))+((cos θ)/(1+sin θ))+((−sin θ)/(λ+cos θ))+((−cos θ)/(λ−sin θ))−((2(−sin θ+cos θ))/(cos θ+sin θ+1)) ((Φ′(θ))/(Φ(θ)))=(cos θ−sin θ)[(((1+cos θ+sin θ)^2 −2(1+cos θ)(1+sin θ))/((1+cos θ)(1+sin θ)))]−(((sin θ+cos θ)(λ+cos θ−sin θ))/((λ+cos θ)(λ−sin θ))) ((Φ′(θ))/(Φ(θ)))=−(((sin θ+cos θ)(λ+cos θ−sin θ))/((λ+cos θ)(λ−sin θ))) Φ′(θ)=0 for R_(max) or R_(min) . (sin θ+cos θ)(λ+cos θ−sin θ)=0 sin θ+cos θ=0 tan θ=−1 ⇒θ=−(π/4) or ((3π)/4) λ+cos θ−sin θ=0 sin θ−cos θ=λ (√2) sin (θ−(π/4))=λ sin (θ−(π/4))=(λ/( (√2))) valid only when (λ/( (√2)))≤1, i.e. λ=((1+μ^2 )/(1−μ^2 ))≤(√2), μ^2 ≤(((√2)−1)/( (√2)+1))=((√2)−1)^2 ⇒μ≤(√2)−1 θ−(π/4)=sin^(−1) (λ/( (√2))) or π−sin^(−1) (λ/( (√2))) ⇒θ=sin^(−1) (λ/( (√2)))+(π/4) or ((5π)/4)−sin^(−1) (λ/( (√2))) R_(max) is at θ=−(π/4): R_(max) =(1/( (√2)))(λ+(1/( (√2))))(((1−μ^2 )(√(a^2 +b^2 )))/(2μ)) R_(max) =((((√2)+1)/( μ))+(μ/( (√2)+1)))((√(a^2 +b^2 ))/4) R_(min) is at θ=((3π)/4), if μ≥(√2)−1: R_(min) =((((√2)−1)/( μ))+(μ/( (√2)−1)))((√(a^2 +b^2 ))/4) R_(min) is at θ=sin^(−1) (λ/( (√2)))+(π/4) or ((5π)/4)−sin^(−1) (λ/( (√2))), if μ≤(√2)−1: R_(min) =((√(a^2 +b^2 ))/2) how to find the circumcenter: eqn. of bisector of AP: y=((b sin θ)/2)−((cos θ+1)/(μ sin θ)) (x−((a(cos θ−1))/2)) eqn. of bisector of BP: y=((b(sin θ−1))/2)−((cos θ)/(μ(1+sin θ)))(x−((a cos θ)/2)) circumcenter C(x_C , y_C ) ((μ(sin θ−1))/2)−((cos θ)/(μ(1+sin θ)))((x_C /a)−((cos θ)/2))=((μ sin θ)/2)−((cos θ+1)/(μ sin θ)) ((x_C /a)−((cos θ−1)/2)) −(μ^2 /2)=((cos θ)/((1+sin θ)))((x_C /a)−((cos θ)/2))−((cos θ+1)/( sin θ)) ((x_C /a)−((cos θ−1)/2)) ((1−μ^2 )/2)=(((cos θ)/(1+sin θ))−((cos θ+1)/( sin θ)))(x_C /a) ⇒(x_C /a)=−(((1−μ^2 )(1+sin θ) sin θ)/(2(1+sin θ+cos θ))) (y_C /a)=((μ(sin θ−1))/2)−((cos θ)/(μ(1+sin θ)))((x_C /a)−((cos θ)/2)) (y_C /a)=(1/(2μ)){((−μ^2 (1−sin θ)(1+sin θ+cos θ)+cos θ−μ^2 sin θ cos θ+cos^2 θ)/((1+sin θ+cos θ)))} ⇒(y_C /a)=(((1−μ^2 )(1+cos θ) cos θ)/(2μ(1+sin θ+cos θ)))](Q164946.png)
Commented by mr W last updated on 23/Jan/22

Commented by mr W last updated on 23/Jan/22

Commented by mr W last updated on 23/Jan/22

Commented by ajfour last updated on 24/Jan/22