a_1 =1 a_2 =−1 and a_n =−a_(n−1) −2a_(n−2) Find a


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 164956 by Jamshidbek last updated on 24/Jan/22

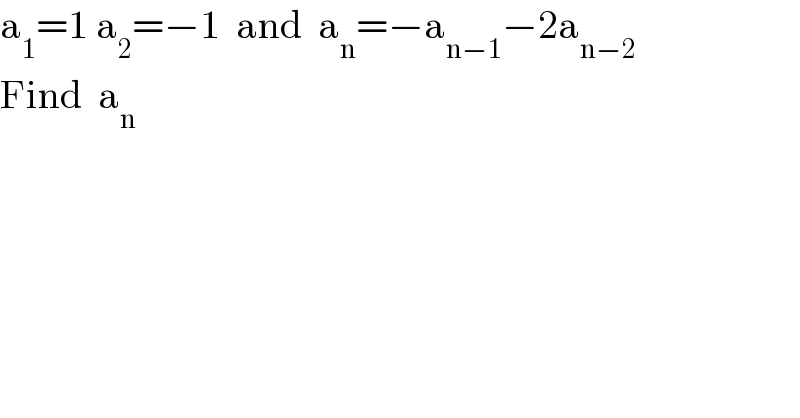
$a_{1} = 1 a_{2} = - 1 and a_{n} = - a_{n - 1} - {2 a}_{n - 2}$ $Find a_{n}$
	Answered by mr W last updated on 24/Jan/22
	$1,−1,0,1,−1,0,1,−1,0,... through “observation”: ⇒a_(3n) =0 ⇒a_(3n+1) =1 ⇒a_(3n+2) =−1 general method: r^2 +r+2=0 r=((−1±i(√3))/2)=−e^(±((πi)/3)) a_n =(−1)^n {Ae^((nπi)/3) +Be^(−((nπi)/3)) } a_2 =−a_1 −2a_0 ⇒−1=−1−2a_0 ⇒a_0 =0 a_0 =A+B=0 a_1 =−{A((1+i(√3))/2)+B((1−i(√3))/2)}=1 A{((1+i(√3))/2)−((1−i(√3))/2)}=−1 A=(i/( (√3)))=(1/( (√3)))e^((πi)/2) =−B a_n =(((−1)^n )/( (√3))){e^(((nπi)/3)+((πi)/2)) −e^(−((nπi)/3)+((πi)/2)) } a_n =(((−1)^n )/( (√3))){cos (((nπ)/3)+(π/2))−cos (−((nπ)/3)+(π/2))+i [sin (((nπ)/3)+(π/2))−sin (−((nπ)/3)+(π/2))]} a_n =(((−1)^n )/( (√3))){−2sin (((nπ)/3))+i [cos (((nπ)/3))−cos (((nπ)/3))} a_n =(((−1)^(n+1) 2 sin (((nπ)/3)))/( (√3)))$
	$1, - 1, 0, 1, - 1, 0, 1, - 1, 0, . . .$ $t h r o u g h ‘ ‘ {o b s e r v a t i o n}^{″} :$ $\Rightarrow a_{3 n} = 0$ $\Rightarrow a_{3 n + 1} = 1$ $\Rightarrow a_{3 n + 2} = - 1$ $g e n e r a l m e t h o d :$ $r^{2} + r + 2 = 0$ $r = \frac{- 1 \pm i \sqrt{3}}{2} = - e^{\pm \frac{π i}{3}}$ $a_{n} = {(- 1)}^{n} {{A e}^{\frac{n π i}{3}} + {B e}^{- \frac{n π i}{3}}}$ $a_{2} = - a_{1} - 2 a_{0} \Rightarrow - 1 = - 1 - 2 a_{0} \Rightarrow a_{0} = 0$ $a_{0} = A + B = 0$ $a_{1} = - {A \frac{1 + i \sqrt{3}}{2} + B \frac{1 - i \sqrt{3}}{2}} = 1$ $A {\frac{1 + i \sqrt{3}}{2} - \frac{1 - i \sqrt{3}}{2}} = - 1$ $A = \frac{i}{\sqrt{3}} = \frac{1}{\sqrt{3}} e^{\frac{π i}{2}} = - B$ $a_{n} = \frac{{(- 1)}^{n}}{\sqrt{3}} {e^{\frac{n π i}{3} + \frac{π i}{2}} - e^{- \frac{n π i}{3} + \frac{π i}{2}}}$ $a_{n} = \frac{{(- 1)}^{n}}{\sqrt{3}} {\cos (\frac{n π}{3} + \frac{π}{2}) - \cos (- \frac{n π}{3} + \frac{π}{2}) + i [\sin (\frac{n π}{3} + \frac{π}{2}) - \sin (- \frac{n π}{3} + \frac{π}{2})]}$ $a_{n} = \frac{{(- 1)}^{n}}{\sqrt{3}} {- 2 \sin (\frac{n π}{3}) + i [\cos (\frac{n π}{3}) - \cos (\frac{n π}{3})}$ $a_{n} = \frac{{(- 1)}^{n + 1} 2 \sin (\frac{n π}{3})}{\sqrt{3}}$
	Commented by solihin last updated on 24/Jan/22

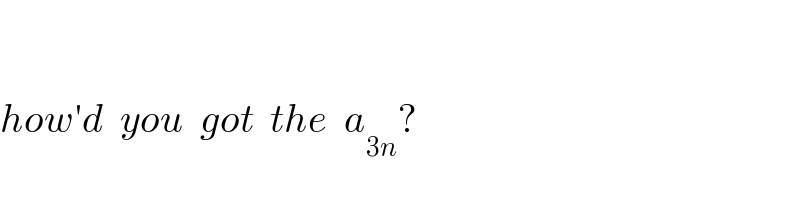
	${h o w}^{'} d y o u g o t t h e a_{3 n} ?$
	Commented by solihin last updated on 24/Jan/22

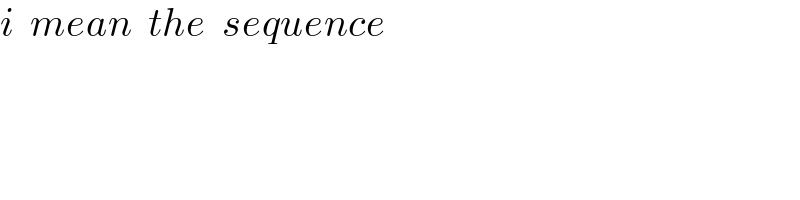
	$i m e a n t h e s e q u e n c e$
	Commented by mr W last updated on 24/Jan/22

	$w i t h a_{1} = 1, a_{2} = - 1 a n d a_{n} = - a_{n - 1} - 2 a_{n - 2}$ $y o u g e t$ $a_{3} = 0$ $a_{4} = 1$ $a_{5} = - 1$ $a_{6} = 0$ $a_{7} = 1$ $a_{8} = - 1$ $a_{9} = 0$ $. . . .$ $t h e n y o u c a n s e e$ $a_{3 n} = 0$ $a_{3 n + 1} = 1$ $a_{3 n + 2} = - 1$ $t h i s i s n o t a n ‘ ‘ {e x a c t}^{″} m e t h o d . i t$ $i s b a s e d o n ‘ ‘ {o b s e r v a t i o n}^{″} .$ $t h e r e f o r e i h a v e g i v e n a s e c o n d a n d$ $m o r e g e n e r a l m e t h o d .$
	Commented by Tawa11 last updated on 24/Jan/22

	$Great sir .$
	Commented by Jamshidbek last updated on 25/Jan/22

	$Mistake$
	Commented by mr W last updated on 25/Jan/22

	$y o u s h o u l d b e m o r e c l e a r s i r! w h a t d o$ $y o u m e a n ? i s t h e r e a m i s t a k e i n t h e$ $q u e s t i o n o r i s t h e r e a m i s t a k e i n m y$ $s o l u t i o n o r w h a t e l s e ?$
	Commented by aleks041103 last updated on 25/Jan/22

	$I t h i n k t h a t y o u c a n a l s o p r o v e t h i s$ $b y i n d u c t i o n .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum