
Question and Answers Forum
Question Number 165063 by MathsFan last updated on 25/Jan/22
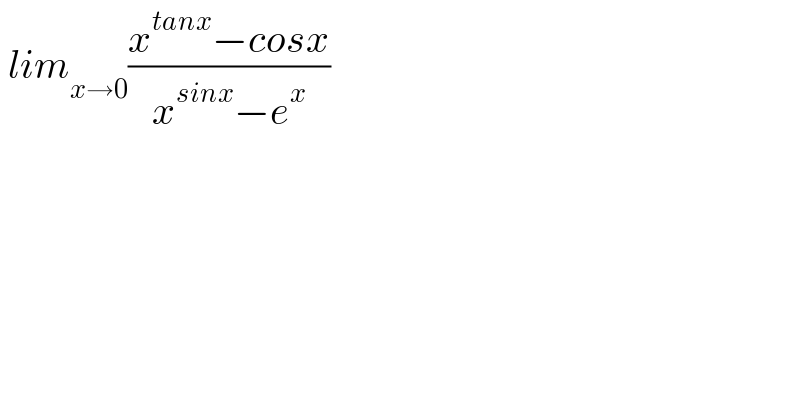
Commented by MathsFan last updated on 25/Jan/22

Answered by aleks041103 last updated on 27/Jan/22
![lim_(x→0) ((x^(tanx) −cosx)/(x^(sinx) −e^x ))=L first we substitute (([0^0 ]−1)/([0^0 ]−1))=? lim_(x→0) x^(tanx) =e^(lim_(x→0) tan(x)ln(x)) lim_(x→0) ((lnx)/(ctgx))=^(l′hopital) lim_(x→0) ((1/x)/(−(1/(sin^2 x))))=−lim_(x→0) ((sin^2 x)/x)= =−lim_(x→0) ((2sin(x)cos(x))/1)=0 ⇒lim_(x→0) x^(tan(x)) =e^0 =1 lim_(x→0) x^(sin(x)) =e^(lim_(x→0) ln(x) sin (x)) lim_(x→0) ln(x)sin(x)=lim_(x→0) ((ln(x))/(1/(sin(x))))= =lim_(x→0) ((1/x)/(−((cos(x))/(sin^2 x))))=−lim_(x→0) ((sin^2 x)/(x cos(x)))=−lim_(x→0) ((sin^2 x)/x)=0 ⇒lim_(x→0) x^(sin(x)) =e^0 =1 ⇒lim_(x→0) ((x^(tanx) −cosx)/(x^(sinx) −e^x ))=[((1−1)/(1−1))]=[(0/0)] tanx→x sinx→x l′hopital (x^x )′=x^x (x ln(x))′=x^x (1+ln(x)) ⇒L=lim_(x→0) ((x^x (1+ln(x))+sin(x))/(x^x (1+ln(x))−e^x ))= =lim_(x→0) ((x^x (1+ln(x)))/(x^x (1+ln(x))−e^x ))=1+lim_(x→0) (e^x /(x^x (1+ln(x))−e^x ))= =1+lim_(x→0) (1/(ln(x)))=1 L=1](Q165197.png)
Commented by aleks041103 last updated on 27/Jan/22

| ||
Question and Answers Forum | ||
Question Number 165063 by MathsFan last updated on 25/Jan/22 | ||
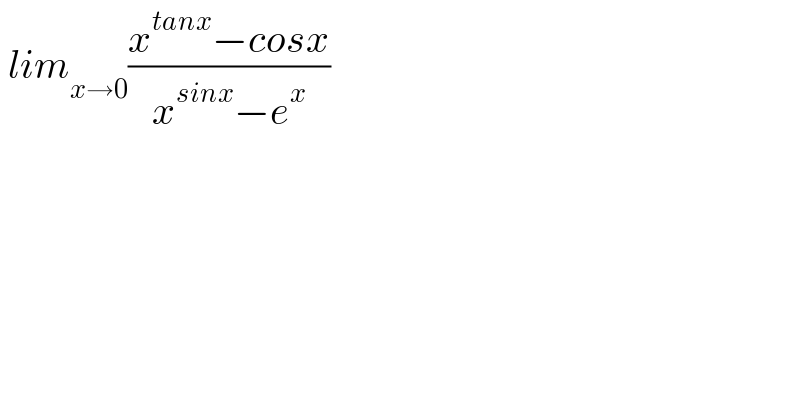 | ||
Commented by MathsFan last updated on 25/Jan/22 | ||
 | ||
Answered by aleks041103 last updated on 27/Jan/22 | ||
![lim_(x→0) ((x^(tanx) −cosx)/(x^(sinx) −e^x ))=L first we substitute (([0^0 ]−1)/([0^0 ]−1))=? lim_(x→0) x^(tanx) =e^(lim_(x→0) tan(x)ln(x)) lim_(x→0) ((lnx)/(ctgx))=^(l′hopital) lim_(x→0) ((1/x)/(−(1/(sin^2 x))))=−lim_(x→0) ((sin^2 x)/x)= =−lim_(x→0) ((2sin(x)cos(x))/1)=0 ⇒lim_(x→0) x^(tan(x)) =e^0 =1 lim_(x→0) x^(sin(x)) =e^(lim_(x→0) ln(x) sin (x)) lim_(x→0) ln(x)sin(x)=lim_(x→0) ((ln(x))/(1/(sin(x))))= =lim_(x→0) ((1/x)/(−((cos(x))/(sin^2 x))))=−lim_(x→0) ((sin^2 x)/(x cos(x)))=−lim_(x→0) ((sin^2 x)/x)=0 ⇒lim_(x→0) x^(sin(x)) =e^0 =1 ⇒lim_(x→0) ((x^(tanx) −cosx)/(x^(sinx) −e^x ))=[((1−1)/(1−1))]=[(0/0)] tanx→x sinx→x l′hopital (x^x )′=x^x (x ln(x))′=x^x (1+ln(x)) ⇒L=lim_(x→0) ((x^x (1+ln(x))+sin(x))/(x^x (1+ln(x))−e^x ))= =lim_(x→0) ((x^x (1+ln(x)))/(x^x (1+ln(x))−e^x ))=1+lim_(x→0) (e^x /(x^x (1+ln(x))−e^x ))= =1+lim_(x→0) (1/(ln(x)))=1 L=1](Q165197.png) | ||
| ||
Commented by aleks041103 last updated on 27/Jan/22 | ||
 | ||