
Previous in Differential Equation Next in Differential Equation
Question Number 16514 by Sai dadon. last updated on 23/Jun/17
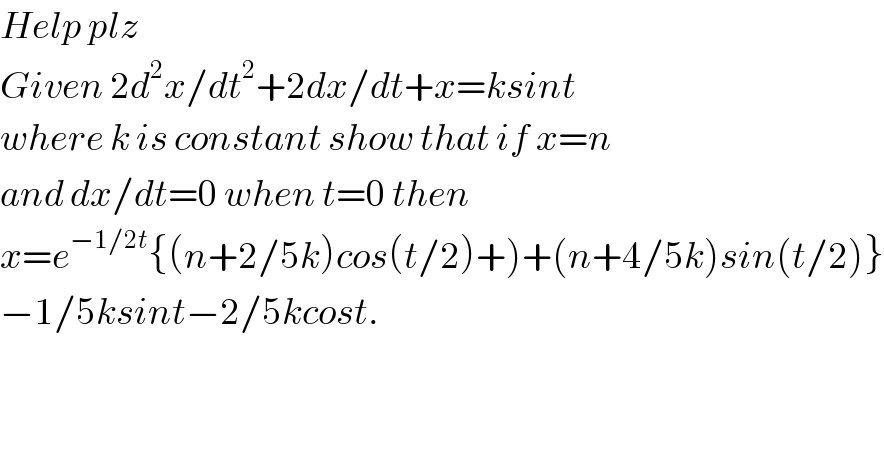
$${Help}\:{plz} \\ $$$${Given}\:\mathrm{2}{d}^{\mathrm{2}} {x}/{dt}^{\mathrm{2}} +\mathrm{2}{dx}/{dt}+{x}={ksint} \\ $$$${where}\:{k}\:{is}\:{constant}\:{show}\:{that}\:{if}\:{x}={n} \\ $$$${and}\:{dx}/{dt}=\mathrm{0}\:{when}\:{t}=\mathrm{0}\:{then}\: \\ $$$$\left.{x}={e}^{−\mathrm{1}/\mathrm{2}{t}} \left\{\left({n}+\mathrm{2}/\mathrm{5}{k}\right){cos}\left({t}/\mathrm{2}\right)+\right)+\left({n}+\mathrm{4}/\mathrm{5}{k}\right){sin}\left({t}/\mathrm{2}\right)\right\} \\ $$$$−\mathrm{1}/\mathrm{5}{ksint}−\mathrm{2}/\mathrm{5}{kcost}. \\ $$
Commented by Sai dadon. last updated on 23/Jun/17

$${I}\:{need}\:{help}\:{guys}. \\ $$
Answered by ajfour last updated on 23/Jun/17
![characteristic equation is: 2λ^2 +2λ+1=0 λ=((−2±(√(4−8)))/4) ⇒ λ_1 =−(1/2)+(i/2) , λ_2 =−(1/2)−(i/2) x_h = e^(−t/2) [Acos (t/2)+Bsin (t/2)] let x_p =Kcos t+Msin t x_p ^′ =−Ksin t+Mcos t x_p ^(′′) =−Kcos t−Msin t =− x_p substituting x=x_p in 2x^(′′) +2x′+x=k sin t −2x_p +2x_p ^′ +x_p = k sin t 2x_p ^′ −x_p =k sin t 2(−Ksin t+Mcos t) −Msin t−Kcos t = k sin t ⇒ 2K+M=−k and 2M−K = 0 or K=2M so, 5M=−k M= −(k/5) and K=−(2/5) x_p = −((2k)/5)cos t−(k/5)sin t the general solution is then x= e^(−t/2) [Acos (t/2)+Bsin (t/2)] −((2k)/5)cos t−(k/5)sin t ...(i) with x=n for t=0 in (i) gives n= A−((2k)/5) ⇒ A = n+((2k)/5) (dx/dt)=−(1/2)e^(−t/2) [Acos (t/2)+Bsin (t/2)] +e^(−t/2) [−(A/2)sin (t/2)+(B/2)cos (t/2)] +((2k)/5)sin t−(k/5)cos t at t=0 we have (dx/dt)=0 , so 0= −(A/2)+(B/2)−(k/5) B= ((2k)/5)+A = ((2k)/5)+n+((2k)/5) B = n+((4k)/5) , we then have x=e^(−t/2) {(n+((2k)/5))cos (t/2)+(n+((4k)/5))sin (t/2)} −(k/5)sin t−((2k)/5)cos t .](Q16539.png)
$$\:{characteristic}\:{equation}\:{is}: \\ $$$$\:\:\mathrm{2}\lambda^{\mathrm{2}} +\mathrm{2}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\:\lambda=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{8}}}{\mathrm{4}}\: \\ $$$$\Rightarrow\:\:\lambda_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}}{\mathrm{2}}\:,\:\lambda_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}−\frac{{i}}{\mathrm{2}} \\ $$$$\:{x}_{{h}} =\:{e}^{−{t}/\mathrm{2}} \left[{A}\mathrm{cos}\:\left({t}/\mathrm{2}\right)+{B}\mathrm{sin}\:\left({t}/\mathrm{2}\right)\right] \\ $$$${let}\:{x}_{{p}} ={K}\mathrm{cos}\:{t}+{M}\mathrm{sin}\:{t} \\ $$$$\:\:\:\:\:\:\:{x}_{{p}} ^{'} =−{K}\mathrm{sin}\:{t}+{M}\mathrm{cos}\:\:{t} \\ $$$$\:\:\:\:\:\:{x}_{{p}} ^{''} =−{K}\mathrm{cos}\:{t}−{M}\mathrm{sin}\:{t}\:=−\:{x}_{{p}} \\ $$$${substituting}\:{x}={x}_{{p}} \:{in} \\ $$$$\:\mathrm{2}{x}^{''} +\mathrm{2}{x}'+{x}={k}\:\mathrm{sin}\:{t} \\ $$$$\:\:−\mathrm{2}{x}_{{p}} +\mathrm{2}{x}_{{p}} ^{'} +{x}_{{p}} =\:{k}\:\mathrm{sin}\:{t} \\ $$$$\:\:\mathrm{2}{x}_{{p}} ^{'} −{x}_{{p}} ={k}\:\mathrm{sin}\:{t} \\ $$$$\:\:\mathrm{2}\left(−{K}\mathrm{sin}\:{t}+{M}\mathrm{cos}\:{t}\right) \\ $$$$\:\:\:\:\:−{M}\mathrm{sin}\:{t}−{K}\mathrm{cos}\:{t}\:=\:{k}\:\mathrm{sin}\:{t} \\ $$$$\Rightarrow\:\:\mathrm{2}{K}+{M}=−{k}\:\:\:\:\:{and} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}{M}−{K}\:=\:\mathrm{0}\:\:\:{or}\:\:{K}=\mathrm{2}{M} \\ $$$$\:{so},\:\:\:\:\:\:\:\mathrm{5}{M}=−{k}\:\:\: \\ $$$$\:\:\:\:\:\:\:{M}=\:−\frac{{k}}{\mathrm{5}}\:\:{and}\:{K}=−\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:{x}_{{p}} =\:−\frac{\mathrm{2}{k}}{\mathrm{5}}\mathrm{cos}\:{t}−\frac{{k}}{\mathrm{5}}\mathrm{sin}\:{t} \\ $$$${the}\:{general}\:{solution}\:{is}\:{then} \\ $$$$\:{x}=\:{e}^{−{t}/\mathrm{2}} \left[{A}\mathrm{cos}\:\left({t}/\mathrm{2}\right)+{B}\mathrm{sin}\:\left({t}/\mathrm{2}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{2}{k}}{\mathrm{5}}\mathrm{cos}\:{t}−\frac{{k}}{\mathrm{5}}\mathrm{sin}\:{t}\:\:\:...\left({i}\right) \\ $$$$\:{with}\:{x}={n}\:\:\:{for}\:{t}=\mathrm{0}\:\:\:\:{in}\:\left({i}\right)\:{gives} \\ $$$${n}=\:{A}−\frac{\mathrm{2}{k}}{\mathrm{5}}\:\:\:\:\:\Rightarrow\:{A}\:=\:{n}+\frac{\mathrm{2}{k}}{\mathrm{5}} \\ $$$$\:\frac{{dx}}{{dt}}=−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{t}/\mathrm{2}} \left[{A}\mathrm{cos}\:\left({t}/\mathrm{2}\right)+{B}\mathrm{sin}\:\left({t}/\mathrm{2}\right)\right] \\ $$$$\:\:+{e}^{−{t}/\mathrm{2}} \left[−\frac{{A}}{\mathrm{2}}\mathrm{sin}\:\left({t}/\mathrm{2}\right)+\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\left({t}/\mathrm{2}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{2}{k}}{\mathrm{5}}\mathrm{sin}\:{t}−\frac{{k}}{\mathrm{5}}\mathrm{cos}\:{t} \\ $$$${at}\:{t}=\mathrm{0}\:\:{we}\:{have}\:\:\frac{{dx}}{{dt}}=\mathrm{0}\:,\:\:{so} \\ $$$$\:\mathrm{0}=\:−\frac{{A}}{\mathrm{2}}+\frac{{B}}{\mathrm{2}}−\frac{{k}}{\mathrm{5}} \\ $$$$\:\:{B}=\:\frac{\mathrm{2}{k}}{\mathrm{5}}+{A}\:=\:\frac{\mathrm{2}{k}}{\mathrm{5}}+{n}+\frac{\mathrm{2}{k}}{\mathrm{5}} \\ $$$$\:\:{B}\:=\:{n}+\frac{\mathrm{4}{k}}{\mathrm{5}}\:,\:{we}\:{then}\:{have} \\ $$$$\:\boldsymbol{{x}}={e}^{−{t}/\mathrm{2}} \left\{\left({n}+\frac{\mathrm{2}{k}}{\mathrm{5}}\right)\mathrm{cos}\:\frac{{t}}{\mathrm{2}}+\left({n}+\frac{\mathrm{4}{k}}{\mathrm{5}}\right)\mathrm{sin}\:\frac{{t}}{\mathrm{2}}\right\} \\ $$$$\:\:\:\:\:\:−\frac{{k}}{\mathrm{5}}\mathrm{sin}\:{t}−\frac{\mathrm{2}{k}}{\mathrm{5}}\mathrm{cos}\:{t}\:. \\ $$
Commented by Sai dadon. last updated on 23/Jun/17

$${Thank}\:{you}\:{aj}. \\ $$$${God}\:{bless}\:{you}. \\ $$
