Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 165296 by ajfour last updated on 28/Jan/22

Commented by ajfour last updated on 28/Jan/22

If when the disc rolls down and is about to to hit the pivot, the rod gets horizontal, find initial angle θ at which system is released. (assume pure rolling throughout)

$${If}\:{when}\:{the}\:{disc}\:{rolls}\:{down}\:{and}\:{is} \\ $$$$\:{about}\:{to}\:{to}\:{hit}\:{the}\:{pivot},\:{the}\:{rod} \\ $$$${gets}\:{horizontal},\:{find}\:{initial}\:{angle} \\ $$$$\theta\:{at}\:{which}\:{system}\:{is}\:{released}. \\ $$$$\left({assume}\:{pure}\:{rolling}\:{throughout}\right) \\ $$

Answered by TheSupreme last updated on 29/Jan/22

locking x Δθ=Δϕ locking θ x=L−ΔϕR x_F =0 Δϕ_F =(L/R)=Δθ θ_0 =θ_F −Δθ=(L/R)

$${locking}\:{x} \\ $$$$\Delta\theta=\Delta\varphi \\ $$$${locking}\:\theta \\ $$$${x}={L}−\Delta\varphi{R} \\ $$$${x}_{{F}} =\mathrm{0} \\ $$$$\Delta\varphi_{{F}} =\frac{{L}}{{R}}=\Delta\theta \\ $$$$\theta_{\mathrm{0}} =\theta_{{F}} −\Delta\theta=\frac{{L}}{{R}} \\ $$

Answered by mr W last updated on 30/Jan/22

Commented by mr W last updated on 29/Jan/22

the common center of mass of both objects (green) remains unchanged in horizontal direction. M×(L/2)=M×(L/2)×cos θ+m×(L cos θ−R sin θ) 1=cos θ+((2m)/M)×(cos θ−(R/L) sin θ) let ξ=1+((2m)/M), λ=((2mR)/(ML)) 1=ξ cos θ−λ sin θ (1/( (√(ξ^2 +λ^2 ))))=(ξ/( (√(ξ^2 +λ^2 ))))×cos θ−(λ/( (√(ξ^2 +λ^2 ))))×sin θ (1/( (√(ξ^2 +λ^2 ))))=cos (θ+φ) θ=cos^(−1) (1/( (√(ξ^2 +λ^2 ))))−tan^(−1) (λ/ξ) ⇒θ=cos^(−1) (1/( (√(1+((4m)/M)+(1+(R^2 /L^2 ))((4m^2 )/M^2 )))))−tan^(−1) (R/((1+(M/(2m)))L)) example: M=m, L=5R θ=cos^(−1) (5/( (√(229))))−tan^(−1) (2/(15))≈63.11°

$${the}\:{common}\:{center}\:{of}\:{mass}\:{of}\:{both} \\ $$$${objects}\:\left({green}\right)\:{remains}\:{unchanged} \\ $$$${in}\:{horizontal}\:{direction}. \\ $$$${M}×\frac{{L}}{\mathrm{2}}={M}×\frac{{L}}{\mathrm{2}}×\mathrm{cos}\:\theta+{m}×\left({L}\:\mathrm{cos}\:\theta−{R}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{1}=\mathrm{cos}\:\theta+\frac{\mathrm{2}{m}}{{M}}×\left(\mathrm{cos}\:\theta−\frac{{R}}{{L}}\:\mathrm{sin}\:\theta\right) \\ $$$${let}\:\xi=\mathrm{1}+\frac{\mathrm{2}{m}}{{M}},\:\lambda=\frac{\mathrm{2}{mR}}{{ML}} \\ $$$$\mathrm{1}=\xi\:\mathrm{cos}\:\theta−\lambda\:\mathrm{sin}\:\theta \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\xi^{\mathrm{2}} +\lambda^{\mathrm{2}} }}=\frac{\xi}{\:\sqrt{\xi^{\mathrm{2}} +\lambda^{\mathrm{2}} }}×\mathrm{cos}\:\theta−\frac{\lambda}{\:\sqrt{\xi^{\mathrm{2}} +\lambda^{\mathrm{2}} }}×\mathrm{sin}\:\theta \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\xi^{\mathrm{2}} +\lambda^{\mathrm{2}} }}=\mathrm{cos}\:\left(\theta+\phi\right) \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\xi^{\mathrm{2}} +\lambda^{\mathrm{2}} }}−\mathrm{tan}^{−\mathrm{1}} \frac{\lambda}{\xi} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{4}{m}}{{M}}+\left(\mathrm{1}+\frac{{R}^{\mathrm{2}} }{{L}^{\mathrm{2}} }\right)\frac{\mathrm{4}{m}^{\mathrm{2}} }{{M}^{\mathrm{2}} }}}−\mathrm{tan}^{−\mathrm{1}} \frac{{R}}{\left(\mathrm{1}+\frac{{M}}{\mathrm{2}{m}}\right){L}} \\ $$$${example}:\:{M}={m},\:{L}=\mathrm{5}{R} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}}{\:\sqrt{\mathrm{229}}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{15}}\approx\mathrm{63}.\mathrm{11}° \\ $$

Commented by Tawa11 last updated on 29/Jan/22

Weldone sir.

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$

Commented by ajfour last updated on 29/Jan/22

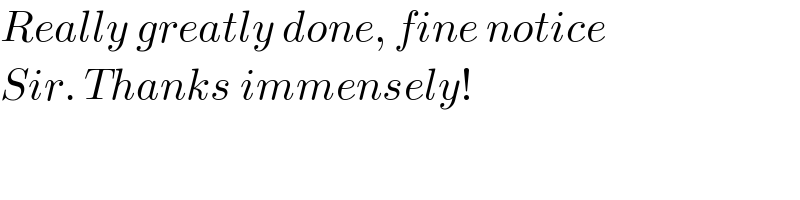
Really greatly done, fine notice Sir. Thanks immensely!

$${Really}\:{greatly}\:{done},\:{fine}\:{notice} \\ $$$${Sir}.\:{Thanks}\:{immensely}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com