
Question and Answers Forum
Question Number 165349 by mkam last updated on 31/Jan/22

Answered by puissant last updated on 31/Jan/22

Commented by puissant last updated on 31/Jan/22
![=lim_(k→∞) Σ_(t=1) ^k arctan(2t+1)−arcan(2t−1) = lim_(t→∞) [arcan(3)−arctan(1)+arctan(5)−arctan(3)+ arctan(7)−arctan(5)....+arctan(2k+1)−arctan(2k−1)] = lim_(k→∞) {−arctan(1)+arctan(2k+1)} = −(π/4)+(π/2) = (π/4).](Q165360.png)
Commented by mkam last updated on 31/Jan/22
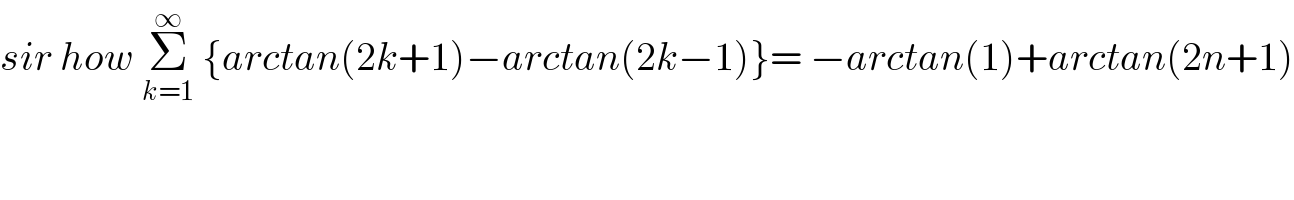
| ||
Question and Answers Forum | ||
Question Number 165349 by mkam last updated on 31/Jan/22 | ||
 | ||
Answered by puissant last updated on 31/Jan/22 | ||
 | ||
| ||
Commented by puissant last updated on 31/Jan/22 | ||
![=lim_(k→∞) Σ_(t=1) ^k arctan(2t+1)−arcan(2t−1) = lim_(t→∞) [arcan(3)−arctan(1)+arctan(5)−arctan(3)+ arctan(7)−arctan(5)....+arctan(2k+1)−arctan(2k−1)] = lim_(k→∞) {−arctan(1)+arctan(2k+1)} = −(π/4)+(π/2) = (π/4).](Q165360.png) | ||
Commented by mkam last updated on 31/Jan/22 | ||
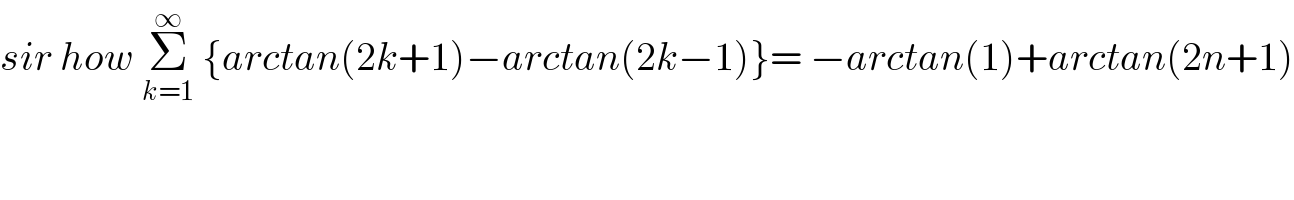 | ||