Question Number 165431 by ajfour last updated on 01/Feb/22
Answered by mr W last updated on 01/Feb/22
Commented by mr W last updated on 01/Feb/22
$${P}\left({p},\:{a}^{\mathrm{2}} −{p}^{\mathrm{2}} \right) \\ $$$${Q}\left({h},\:{r}\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }},\:\mathrm{sin}\:\theta=\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$${r}={a}^{\mathrm{2}} −{p}^{\mathrm{2}} +{r}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{r}=\frac{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}} \\ $$$${h}={p}+{r}\:\mathrm{sin}\:\theta={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$${tangent}\:{line}:\:{y}={c}+{mx} \\ $$$${m}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\frac{\mathrm{1}}{\mathrm{2}{p}} \\ $$$${y}={c}+\frac{{x}}{\mathrm{2}{p}} \\ $$$${c}+\frac{{x}}{\mathrm{2}{p}}={a}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\frac{{x}}{\mathrm{2}{p}}+{c}−{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta=\frac{\mathrm{1}}{\mathrm{4}{p}^{\mathrm{2}} }−\mathrm{4}\left({c}−{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{16}{p}^{\mathrm{2}} }+{a}^{\mathrm{2}} \\ $$$$\frac{{x}}{\mathrm{2}{p}}−{y}+\frac{\mathrm{1}}{\mathrm{16}{p}^{\mathrm{2}} }+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${r}=\frac{\mid\frac{\mathrm{1}}{\mathrm{2}{p}}\left({p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\right)−{r}+\frac{\mathrm{1}}{\mathrm{16}{p}^{\mathrm{2}} }+{a}^{\mathrm{2}} \mid}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{p}^{\mathrm{2}} }}} \\ $$$${r}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{p}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}{p}}\left({p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\right)−{r}+\frac{\mathrm{1}}{\mathrm{16}{p}^{\mathrm{2}} }+{a}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\left({a}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }−\mathrm{1}}\left(\frac{\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}{\mathrm{2}{p}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{16}{p}^{\mathrm{2}} }+{a}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 01/Feb/22
Commented by ajfour last updated on 01/Feb/22
$${But}\:{sir},\:{in}\:{your}\:{solution} \\ $$$$\:\:{r}={f}\left({p}\right)\:,\:{p}\:{isnt}\:{determined} \\ $$$$\:{though}... \\ $$
Commented by mr W last updated on 01/Feb/22
$${i}\:{can}\:{only}\:{get}\:{an}\:{equation}\:{for}\:{p}, \\ $$$${which}\:{can}\:{be}\:{solved}\:{numerically} \\ $$$${for}\:{a}\:{given}\:{a}.\:{with}\:{this}\:{p}\:{we}\:{can}\: \\ $$$${calculate}\:{r}. \\ $$$${i}\:{can}'{t}\:{find}\:{an}\:{equation}\:{directly}\:{for} \\ $$$${r}. \\ $$
Commented by mr W last updated on 01/Feb/22
$${or}\:{we}\:{can}\:{take}\:{p}\:{as}\:{parameter}\:{and} \\ $$$${show}\:{the}\:{relationship}\:{between}\:{a} \\ $$$${and}\:{r}: \\ $$
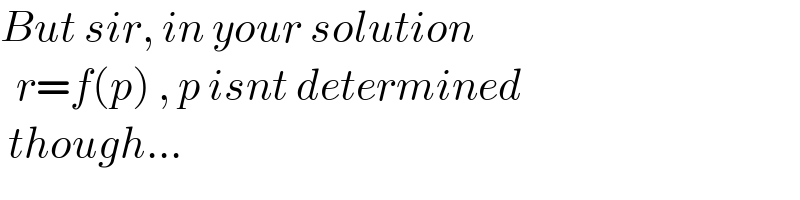
Commented by mr W last updated on 01/Feb/22
Commented by ajfour last updated on 01/Feb/22
Yeah, even i tried n got two eqns. in r, p, a. Thanks sir, i shall chase it bit more..
Commented by Tawa11 last updated on 02/Feb/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 02/Feb/22
Commented by ajfour last updated on 02/Feb/22
![y=(x/(2p))+c=a^2 −x^2 (tan θ=(1/(2p))) ⇒ x^2 +(x/(2p))+c−a^2 =0 x=p=−(1/(4p))+(√((1/(16p^2 ))+a^2 −c)) ⇒ p^2 +(1/2)=a^2 −c ⇒ c=a^2 −((1/2)+p^2 ) ..(i) Now r−rsin θ=r−(r/( (√(1+4p^2 )))) =a^2 −p^2 ⇒ r=((a^2 −p^2 )/(1−(1/( (√(1+4p^2 )))))) ...(ii) consider upper line y=(x/(2p))+c+rsec θ [now with ..(i)] a^2 −x^2 = (x/(2p))+a^2 −((1/2)+p^2 )+((r(√(1+4p^2 )))/(2p)) D=0 ⇒ (1/(4p^2 ))=((2r(√(1+4p^2 )))/p)−(2+4p^2 ) using ..(ii) (1/(4p^2 ))=((2(√(1+4p^2 )))/p)(((a^2 −p^2 )/(1−(1/( (√(1+4p^2 )))))))−(2+4p^2 ) ⇒ (2p+(1/(2p)))(√(2p))=((4(a^2 −p^2 ))/( (√((1/(2p))+2p))−(1/( (√(2p)))))) And r=((a^2 −p^2 )/(1−(1/( (√(1+4p^2 )))))) .](Q165492.png)
$${y}=\frac{{x}}{\mathrm{2}{p}}+{c}={a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:\:\:\:\:\:\left(\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{p}}\right) \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} +\frac{{x}}{\mathrm{2}{p}}+{c}−{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}={p}=−\frac{\mathrm{1}}{\mathrm{4}{p}}+\sqrt{\frac{\mathrm{1}}{\mathrm{16}{p}^{\mathrm{2}} }+{a}^{\mathrm{2}} −{c}} \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}={a}^{\mathrm{2}} −{c} \\ $$$$\Rightarrow\:\:{c}={a}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}+{p}^{\mathrm{2}} \right)\:\:\:\:\:..\left({i}\right) \\ $$$${Now} \\ $$$${r}−{r}\mathrm{sin}\:\theta={r}−\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:={a}^{\mathrm{2}} −{p}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{r}=\frac{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}\:\:\:\:\:\:\:...\left({ii}\right) \\ $$$${consider}\:{upper}\:{line} \\ $$$$\:\:\:{y}=\frac{{x}}{\mathrm{2}{p}}+{c}+{r}\mathrm{sec}\:\theta\:\:\:\:\left[{now}\:{with}\:..\left({i}\right)\right] \\ $$$$\:\:{a}^{\mathrm{2}} −{x}^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\frac{{x}}{\mathrm{2}{p}}+{a}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}+{p}^{\mathrm{2}} \right)+\frac{{r}\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}{\mathrm{2}{p}} \\ $$$${D}=\mathrm{0}\:\:\Rightarrow \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{4}{p}^{\mathrm{2}} }=\frac{\mathrm{2}{r}\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}{{p}}−\left(\mathrm{2}+\mathrm{4}{p}^{\mathrm{2}} \right) \\ $$$${using}\:\:..\left({ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{p}^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}{{p}}\left(\frac{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}\right)−\left(\mathrm{2}+\mathrm{4}{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow \\ $$$$\:\left(\mathrm{2}{p}+\frac{\mathrm{1}}{\mathrm{2}{p}}\right)\sqrt{\mathrm{2}{p}}=\frac{\mathrm{4}\left({a}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}{p}}+\mathrm{2}{p}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{p}}}} \\ $$$${And}\:\:\:{r}=\frac{{a}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}\:\:. \\ $$
Commented by ajfour last updated on 02/Feb/22
$${a}=\mathrm{2}\:,\:{p}\approx\mathrm{1}.\mathrm{4906}\:\:,\:{r}\:\approx\:\mathrm{2}.\mathrm{60728} \\ $$$${a}=\mathrm{3},\:{p}\approx\mathrm{2}.\mathrm{21163}\:,\:{r}\approx\mathrm{5}.\mathrm{27102} \\ $$
Commented by mr W last updated on 02/Feb/22
$${very}\:{fine}\:{sir}! \\ $$
Commented by ajfour last updated on 02/Feb/22
