Question and Answers Forum

All Questions      Topic List

Logic Questions

Previous in All Question      Next in All Question      

Previous in Logic      Next in Logic      

Question Number 1656 by Rasheed Soomro last updated on 29/Aug/15

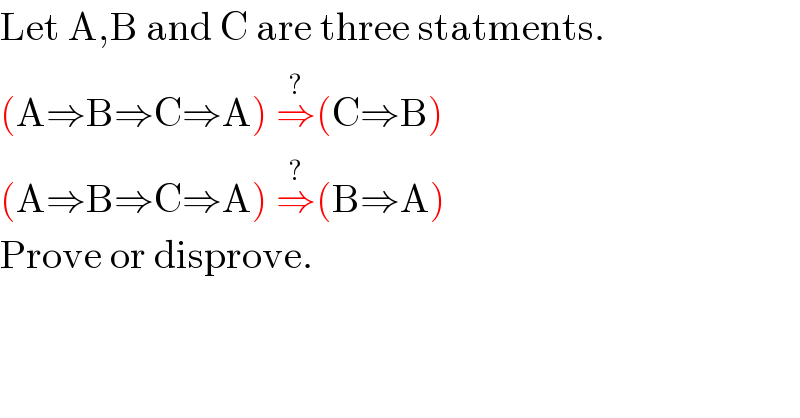
Let A,B and C are three statments. (A⇒B⇒C⇒A) ⇒^(?) (C⇒B) (A⇒B⇒C⇒A) ⇒^(?) (B⇒A) Prove or disprove.

$$\mathrm{Let}\:\mathrm{A},\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{are}\:\mathrm{three}\:\mathrm{statments}.\: \\ $$$$\left(\mathrm{A}\Rightarrow\mathrm{B}\Rightarrow\mathrm{C}\Rightarrow\mathrm{A}\right)\:\overset{?} {\Rightarrow}\left(\mathrm{C}\Rightarrow\mathrm{B}\right)\: \\ $$$$\left(\mathrm{A}\Rightarrow\mathrm{B}\Rightarrow\mathrm{C}\Rightarrow\mathrm{A}\right)\:\overset{?} {\Rightarrow}\left(\mathrm{B}\Rightarrow\mathrm{A}\right)\: \\ $$$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{disprove}. \\ $$

Commented by Yozzian last updated on 29/Aug/15

The best approach to showing whether or not those statements are tautologies or contradictions is by use of truth tables.

$${The}\:{best}\:{approach}\:{to}\:{showing} \\ $$$${whether}\:{or}\:{not}\:{those}\:{statements} \\ $$$${are}\:{tautologies}\:{or}\:{contradictions} \\ $$$${is}\:{by}\:{use}\:{of}\:{truth}\:{tables}. \\ $$

Commented by 112358 last updated on 29/Aug/15

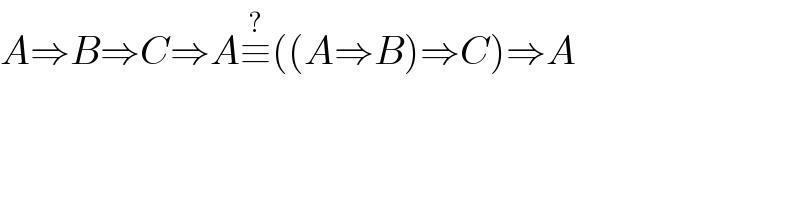
A⇒B⇒C⇒A≡^? ((A⇒B)⇒C)⇒A

$${A}\Rightarrow{B}\Rightarrow{C}\Rightarrow{A}\overset{?} {\equiv}\left(\left({A}\Rightarrow{B}\right)\Rightarrow{C}\right)\Rightarrow{A} \\ $$

Commented by Yozzy last updated on 29/Aug/15

Let p=(A⇒B⇒C⇒A)⇒(C⇒B) r=(A⇒B⇒C⇒A)⇒(B⇒A) I′m assuming that A⇒B⇒C⇒A≡((A⇒B)⇒C)⇒A≡(A⇒B)⇒(C⇒A) . Let q=(A⇒B)⇒(C⇒A) 1 2 3 4 5 6 7 8 9 10 11 12 (column numbers) A∣B∣C∣A⇒B∣(A⇒B)⇒C∣((A⇒B)⇒C)⇒A∣ C⇒B∣ p∣C⇒A∣q ∣B⇒A∣ r 0∣ 0 ∣0 1 0 1 1 1 1 1 1 1 0∣ 0 ∣1 1 1 0 0 1 0 0 1 1 0∣ 1 ∣0 1 0 1 1 1 1 1 0 0 0∣ 1 ∣1 1 1 0 1 1 0 0 0 1 1∣ 0 ∣0 0 1 1 1 1 1 1 1 1 1∣ 0 ∣1 0 1 1 0 0 1 1 1 1 1∣ 1 ∣0 1 0 1 1 1 1 1 1 1 1∣ 1 ∣1 1 1 1 1 1 1 1 1 1 (1 indicates a statement is true while 0 indicates a statement is false.) From the above truth table column 8, we have that p=(A⇒B⇒C⇒A)⇒(C⇒B)≡1 if we have any logic combination of A,B and C other than A=1,B=0,C=1. By Boolean algebra, p=(1⇒0⇒1⇒1)⇒(1⇒0) =(0⇒1⇒1)⇒0 =(1⇒1)⇒0 =∽(1⇒1)∨0 =∽1∨0 =0∨0 p=0 (A⇒B⇒C⇒⇒A)⇏(C⇒B) if A is true,B is false and C is true. Also, column 12 shows that (A⇒B⇒C⇒A)⇒(B⇒A) is false iff A=0 , B=1 and C=0.

$${Let}\:{p}=\left({A}\Rightarrow{B}\Rightarrow{C}\Rightarrow{A}\right)\Rightarrow\left({C}\Rightarrow{B}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:{r}=\left({A}\Rightarrow{B}\Rightarrow{C}\Rightarrow{A}\right)\Rightarrow\left({B}\Rightarrow{A}\right) \\ $$$${I}'{m}\:{assuming}\:{that}\:{A}\Rightarrow{B}\Rightarrow{C}\Rightarrow{A}\equiv\left(\left({A}\Rightarrow{B}\right)\Rightarrow{C}\right)\Rightarrow{A}\equiv\left({A}\Rightarrow{B}\right)\Rightarrow\left({C}\Rightarrow{A}\right)\:. \\ $$$${Let}\:{q}=\left({A}\Rightarrow{B}\right)\Rightarrow\left({C}\Rightarrow{A}\right)\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{1}\:\:\:\mathrm{2}\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}\:\:\:\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\mathrm{9}\:\:\:\:\:\:\:\:\mathrm{10}\:\:\:\:\:\:\mathrm{11}\:\:\:\:\mathrm{12}\:\left({column}\:{numbers}\right) \\ $$$${A}\mid{B}\mid{C}\mid{A}\Rightarrow{B}\mid\left({A}\Rightarrow{B}\right)\Rightarrow{C}\mid\left(\left({A}\Rightarrow{B}\right)\Rightarrow{C}\right)\Rightarrow{A}\mid\:{C}\Rightarrow{B}\mid\:{p}\mid{C}\Rightarrow{A}\mid{q}\:\:\mid{B}\Rightarrow{A}\mid\:{r} \\ $$$$\mathrm{0}\mid\:\:\mathrm{0}\:\mid\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{0}\mid\:\:\mathrm{0}\:\mid\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{0}\mid\:\:\mathrm{1}\:\mid\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\mathrm{0}\mid\:\:\mathrm{1}\:\mid\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\mid\:\:\mathrm{0}\:\mid\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\mid\:\:\mathrm{0}\:\mid\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\mid\:\:\mathrm{1}\:\mid\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\mid\:\:\mathrm{1}\:\mid\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\left(\mathrm{1}\:{indicates}\:{a}\:{statement}\:{is}\:{true}\:{while}\:\mathrm{0}\:{indicates}\:{a}\:{statement}\:{is}\:{false}.\right) \\ $$$${From}\:{the}\:{above}\:{truth}\:{table}\:{column}\:\mathrm{8},\:{we}\:{have}\:{that}\:{p}=\left({A}\Rightarrow{B}\Rightarrow{C}\Rightarrow{A}\right)\Rightarrow\left({C}\Rightarrow{B}\right)\equiv\mathrm{1}\:{if}\:{we} \\ $$$${have}\:{any}\:{logic}\:{combination}\:{of}\:{A},{B}\:{and}\:{C}\:{other}\:{than}\:{A}=\mathrm{1},{B}=\mathrm{0},{C}=\mathrm{1}. \\ $$$${By}\:{Boolean}\:{algebra},\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{p}=\left(\mathrm{1}\Rightarrow\mathrm{0}\Rightarrow\mathrm{1}\Rightarrow\mathrm{1}\right)\Rightarrow\left(\mathrm{1}\Rightarrow\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{0}\Rightarrow\mathrm{1}\Rightarrow\mathrm{1}\right)\Rightarrow\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{1}\Rightarrow\mathrm{1}\right)\Rightarrow\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\backsim\left(\mathrm{1}\Rightarrow\mathrm{1}\right)\vee\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\backsim\mathrm{1}\vee\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\vee\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{p}=\mathrm{0} \\ $$$$\left({A}\Rightarrow{B}\Rightarrow{C}\Rightarrow\Rightarrow{A}\right)\nRightarrow\left({C}\Rightarrow{B}\right)\:{if}\:{A}\:{is}\:{true},{B}\:{is}\:{false}\:{and}\:{C}\:{is}\:{true}. \\ $$$${Also},\:{column}\:\mathrm{12}\:{shows}\:{that}\:\left({A}\Rightarrow{B}\Rightarrow{C}\Rightarrow{A}\right)\Rightarrow\left({B}\Rightarrow{A}\right)\:{is}\:{false}\:{iff}\:{A}=\mathrm{0}\:, \\ $$$${B}=\mathrm{1}\:{and}\:{C}=\mathrm{0}. \\ $$

Commented by Rasheed Soomro last updated on 30/Aug/15

Thanks for so much labour. I have not been much involved in logic. So if you see no meaning in my questions please excuse me. Is there a transitive law of implication? A⇒B ,B⇒C then A⇒C ? ′If A is true then B is true′ ,′ If B is true then C is true′ ⇒ ′If A is true then C is true′ ? Can we write A⇒B⇒C⇒A in place of A⇒B, B⇒C,C⇒A ?

$$\boldsymbol{\mathrm{Thanks}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{much}}\:\boldsymbol{\mathrm{labour}}. \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{not}\:\mathrm{been}\:\mathrm{much}\:\:\mathrm{involved}\:\mathrm{in}\:\mathrm{logic}.\: \\ $$$$\mathrm{So}\:\:\mathrm{if}\:\mathrm{you}\:\mathrm{see}\:\mathrm{no}\:\mathrm{meaning}\:\mathrm{in}\:\mathrm{my}\:\mathrm{questions}\:\mathrm{please}\:\mathrm{excuse} \\ $$$$\mathrm{me}.\: \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{transitive}\:\mathrm{law}\:\mathrm{of}\:\mathrm{implication}? \\ $$$$\mathrm{A}\Rightarrow\mathrm{B}\:,\mathrm{B}\Rightarrow\mathrm{C}\:\mathrm{then}\:\mathrm{A}\Rightarrow\mathrm{C}\:? \\ $$$$'\mathrm{If}\:\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{then}\:\mathrm{B}\:\mathrm{is}\:\mathrm{true}'\:,'\:\mathrm{If}\:\mathrm{B}\:\mathrm{is}\:\mathrm{true}\:\mathrm{then}\:\mathrm{C}\:\mathrm{is}\:\mathrm{true}' \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow \\ $$$$\:'\mathrm{If}\:\mathrm{A}\:\mathrm{is}\:\mathrm{true}\:\mathrm{then}\:\mathrm{C}\:\mathrm{is}\:\mathrm{true}'\:\:\:? \\ $$$$\mathrm{Can}\:\mathrm{we}\:\mathrm{write}\:\mathrm{A}\Rightarrow\mathrm{B}\Rightarrow\mathrm{C}\Rightarrow\mathrm{A}\:\mathrm{in}\:\mathrm{place}\:\mathrm{of} \\ $$$$\mathrm{A}\Rightarrow\mathrm{B},\:\mathrm{B}\Rightarrow\mathrm{C},\mathrm{C}\Rightarrow\mathrm{A}\:\:?\:\: \\ $$

Commented by Yozzy last updated on 30/Aug/15

Propose that p=A⇒B,q=B⇒C and r=A⇒C . To prove there being a transitive property of implication is like saying (I think) to show that [(A⇒B)∧(B⇒C)]⇒(A⇒C)=T, i.e (p∧q)⇒r is a tautology. Without truth tables, I′ll attempt to use the laws of Boolean algebra to simplify the logic expression to hopefully end up having a tautology. Note that μ⇒z≡∽μ∨z. [(A⇒B)∧(B⇒C)]⇒(A⇒C)≡[(∽A∨B)∧(∽B∨C)]⇒(∽A∨C) lhs≡∽[(∽A∨B)∧(∽B∨C)]∨(∽A∨C) lhs≡[∽(∽A∨B)∨∽(∽B∨C)]∨(∽A∨C) De Morgan′s law lhs≡[(A∧∽B)∨(B∧∽C)]∨(∽A∨C) De Morgan′s law, Double negation law lhs≡[∽A∨(A∧∽B)]∨[C∨(B∧∽C)] Commutative law,Associative law lhs≡[(∽A∨A)∧(∽A∨∽B)]∨[(C∨B)∧(C∨∽C)] Distribution law lhs≡[T∧(∽A∨∽B)]∨[(C∨B)∧T] Complementary law lhs≡(∽A∨∽B)∨(C∨B) Identity law lhs≡(∽B∨B)∨(C∨∽A) Commutative law,Associative law lhs≡T∨(C∨∽A) Complementary law lhs≡T Domination law The simplification of the Boolean statement has given us a constant truth value of T, so the statement is perpetually true. Hence,a transitive property of the implication logic as been proven. ■

$${Propose}\:{that}\:{p}={A}\Rightarrow{B},{q}={B}\Rightarrow{C}\:{and}\:{r}={A}\Rightarrow{C}\:. \\ $$$${To}\:{prove}\:{there}\:{being}\:{a}\:{transitive}\:{property}\:{of}\:{implication}\:{is}\:{like}\:{saying}\:\left({I}\:{think}\right)\:{to}\: \\ $$$${show}\:{that}\:\left[\left({A}\Rightarrow{B}\right)\wedge\left({B}\Rightarrow{C}\right)\right]\Rightarrow\left({A}\Rightarrow{C}\right)={T},\:{i}.{e}\:\left({p}\wedge{q}\right)\Rightarrow{r}\:\:{is}\:{a}\:{tautology}. \\ $$$${Without}\:{truth}\:{tables},\:{I}'{ll}\:{attempt}\:{to}\:{use}\:{the}\:{laws}\:{of}\:{Boolean}\:{algebra} \\ $$$${to}\:{simplify}\:{the}\:{logic}\:{expression}\:{to}\:{hopefully}\:{end}\:{up}\:{having}\:{a}\:{tautology}. \\ $$$${Note}\:{that}\:\mu\Rightarrow{z}\equiv\backsim\mu\vee{z}. \\ $$$$\left[\left({A}\Rightarrow{B}\right)\wedge\left({B}\Rightarrow{C}\right)\right]\Rightarrow\left({A}\Rightarrow{C}\right)\equiv\left[\left(\backsim{A}\vee{B}\right)\wedge\left(\backsim{B}\vee{C}\right)\right]\Rightarrow\left(\backsim{A}\vee{C}\right) \\ $$$${lhs}\equiv\backsim\left[\left(\backsim{A}\vee{B}\right)\wedge\left(\backsim{B}\vee{C}\right)\right]\vee\left(\backsim{A}\vee{C}\right) \\ $$$${lhs}\equiv\left[\backsim\left(\backsim{A}\vee{B}\right)\vee\backsim\left(\backsim{B}\vee{C}\right)\right]\vee\left(\backsim{A}\vee{C}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{De}\:{Morgan}'{s}\:{law} \\ $$$${lhs}\equiv\left[\left({A}\wedge\backsim{B}\right)\vee\left({B}\wedge\backsim{C}\right)\right]\vee\left(\backsim{A}\vee{C}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{De}\:{Morgan}'{s}\:{law},\:{Double}\:{negation}\:{law} \\ $$$${lhs}\equiv\left[\backsim{A}\vee\left({A}\wedge\backsim{B}\right)\right]\vee\left[{C}\vee\left({B}\wedge\backsim{C}\right)\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Commutative}\:{law},{Associative}\:{law} \\ $$$${lhs}\equiv\left[\left(\backsim{A}\vee{A}\right)\wedge\left(\backsim{A}\vee\backsim{B}\right)\right]\vee\left[\left({C}\vee{B}\right)\wedge\left({C}\vee\backsim{C}\right)\right]\:\:\:\:{Distribution}\:{law} \\ $$$${lhs}\equiv\left[{T}\wedge\left(\backsim{A}\vee\backsim{B}\right)\right]\vee\left[\left({C}\vee{B}\right)\wedge{T}\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Complementary}\:{law} \\ $$$${lhs}\equiv\left(\backsim{A}\vee\backsim{B}\right)\vee\left({C}\vee{B}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Identity}\:{law} \\ $$$${lhs}\equiv\left(\backsim{B}\vee{B}\right)\vee\left({C}\vee\backsim{A}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Commutative}\:{law},{Associative}\:{law} \\ $$$${lhs}\equiv{T}\vee\left({C}\vee\backsim{A}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Complementary}\:{law} \\ $$$${lhs}\equiv{T}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Domination}\:{law}\: \\ $$$${The}\:{simplification}\:{of}\:{the}\:{Boolean}\:{statement}\:{has}\:{given}\:{us}\:{a}\:{constant} \\ $$$${truth}\:{value}\:{of}\:{T},\:{so}\:{the}\:{statement}\:{is}\:{perpetually}\:{true}.\:{Hence},{a}\:{transitive} \\ $$$${property}\:{of}\:{the}\:{implication}\:{logic}\:{as}\:{been}\:{proven}.\:\blacksquare \\ $$$$ \\ $$

Commented by Yozzy last updated on 30/Aug/15

A∣B∣C∣A⇒B∣B⇒C∣A⇒C∣(A⇒B)∧(B⇒C)∣[(A⇒B)∧(B⇒C)]⇒(A⇒C) 0 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 0 1 0 0 0 1 1 1 1 1 1 1 1 1 The last column to the right indicates that the statement [(A⇒B)∧(B⇒C)]⇒(A⇒C) is always true. Therefore, this proves the existance of a transitive property of the implication logic. (I′ll check over my Boolean simplification.Checked.)

$${A}\mid{B}\mid{C}\mid{A}\Rightarrow{B}\mid{B}\Rightarrow{C}\mid{A}\Rightarrow{C}\mid\left({A}\Rightarrow{B}\right)\wedge\left({B}\Rightarrow{C}\right)\mid\left[\left({A}\Rightarrow{B}\right)\wedge\left({B}\Rightarrow{C}\right)\right]\Rightarrow\left({A}\Rightarrow{C}\right) \\ $$$$\mathrm{0}\:\:\:\:\mathrm{0}\:\:\mathrm{0}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{0}\:\:\:\:\mathrm{0}\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{0}\:\:\:\:\mathrm{1}\:\:\mathrm{0}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{0}\:\:\:\:\mathrm{1}\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\:\:\:\:\mathrm{0}\:\:\mathrm{0}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\:\:\:\:\mathrm{0}\:\:\mathrm{1}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\:\:\:\:\mathrm{1}\:\:\mathrm{0}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{1}\:\:\:\:\mathrm{1}\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$${The}\:{last}\:{column}\:{to}\:{the}\:{right}\:{indicates}\:{that}\:{the}\:{statement} \\ $$$$\left[\left({A}\Rightarrow{B}\right)\wedge\left({B}\Rightarrow{C}\right)\right]\Rightarrow\left({A}\Rightarrow{C}\right)\:{is}\:{always}\:{true}.\:{Therefore},\:{this}\:{proves} \\ $$$${the}\:{existance}\:{of}\:{a}\:{transitive}\:{property}\:{of}\:{the}\:{implication}\:{logic}. \\ $$$$\left({I}'{ll}\:{check}\:{over}\:{my}\:{Boolean}\:{simplification}.{Checked}.\right) \\ $$

Commented by Rasheed Soomro last updated on 30/Aug/15

THANKSSsssssss! Yozzian=^(?) Yozzy

$$\boldsymbol{\mathrm{THANKS}}\mathrm{Ss}{ssssss}! \\ $$$$\mathrm{Yozzian}\overset{?} {=}\mathrm{Yozzy} \\ $$

Commented by Yozzy last updated on 30/Aug/15

I use my cell phones (2) and my tablet. I′ve been the only one commenting on this question. I used my tablet to answer the question because of the long truth table.

$${I}\:{use}\:{my}\:{cell}\:{phones}\:\left(\mathrm{2}\right)\:{and}\:{my}\:{tablet}.\:{I}'{ve}\:{been}\:{the}\:{only}\:{one}\:{commenting} \\ $$$${on}\:{this}\:{question}.\:{I}\:{used}\:{my}\:{tablet}\:{to}\:{answer}\:{the}\:{question}\:{because}\:{of}\:{the} \\ $$$${long}\:{truth}\:{table}. \\ $$

Commented by Rasheed Soomro last updated on 30/Aug/15

I have also more than one device and I use two ID′s: Rasheed Soomro and Rasheed Ahmad

$${I}\:{have}\:{also}\:{more}\:{than}\:{one}\:{device}\:{and}\:{I}\:{use}\:{two}\:{ID}'{s}: \\ $$$$\mathrm{Rasheed}\:\mathrm{Soomro}\:\:\:\:\:{and}\:\:\:\:\:\:\:\:\mathrm{Rasheed}\:\mathrm{Ahmad} \\ $$

Commented by 112358 last updated on 30/Aug/15

I see.

$${I}\:{see}. \\ $$

Commented by 123456 last updated on 30/Aug/15

XD 2^n_i

$$\mathrm{XD}\:\mathrm{2}^{{n}_{{i}} } \\ $$

Commented by Rasheed Ahmad last updated on 30/Aug/15

XD 2^n_i ???

$$\mathrm{XD}\:\mathrm{2}^{{n}_{{i}} } \:??? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com