Question Number 165780 by MWSuSon last updated on 08/Feb/22
$$\mathrm{Mr}\:\mathrm{and}\:\mathrm{Mr}\:\mathrm{young}\:\mathrm{borrowed}\:\mathrm{Z}\:\mathrm{amount}\:\mathrm{of}\:\mathrm{money}\:\mathrm{from} \\ $$$$\mathrm{a}\:\mathrm{bank}\:\mathrm{at}\:\mathrm{a}\:\mathrm{daily}\:\mathrm{interest}\:\mathrm{rate}\:\mathrm{r}.\:\mathrm{The}\:\mathrm{youngs}\:\mathrm{make}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{micro}\:\mathrm{payment}\:\mathrm{of}\:\mathrm{D}\:\mathrm{amount}\:\mathrm{to}\:\mathrm{the}\:\mathrm{bank}\:\mathrm{each}\:\mathrm{day}. \\ $$$$\:\mathrm{Set}\:\mathrm{up}\:\mathrm{a}\:\mathrm{differential}\:\mathrm{equation}\:\mathrm{for}\:\mathrm{amount}\:\mathrm{x}\:\mathrm{owed} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{bank}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}\:\mathrm{of}\:\mathrm{the}\:\mathrm{each}\:\mathrm{day}\:\mathrm{after}\:\mathrm{the}\:\mathrm{loan} \\ $$$$\mathrm{closing}. \\ $$
Commented by MWSuSon last updated on 08/Feb/22
$$\mathrm{How}\:\mathrm{do}\:\mathrm{i}\:\mathrm{set}\:\mathrm{up}\:\mathrm{a}\:\mathrm{differential}\:\mathrm{equation}\:\mathrm{concerning} \\ $$$$\mathrm{this}\:\mathrm{question}\:\mathrm{sir}? \\ $$
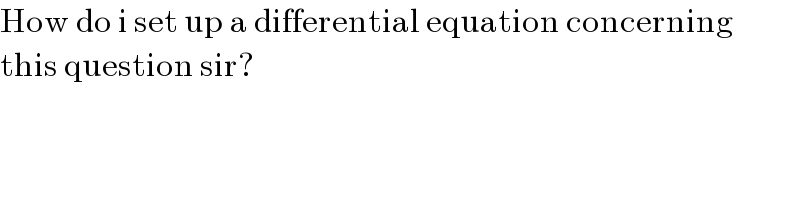
Commented by mr W last updated on 08/Feb/22
$${the}\:{same}\:{as}\:{Q}\mathrm{165404} \\ $$
Commented by mr W last updated on 08/Feb/22
![loan: Z daily interest rate: r daily pay back: D after t days the Youngs owe the bank money x. t as discrete variable: from Q165404 we have x=Z(1+r)^t −((D[(1+r)^t −1])/r) x=(D/r)+(Z−(D/r))(1+r)^t](Q165796.png)
$${loan}:\:{Z} \\ $$$${daily}\:{interest}\:{rate}:\:{r} \\ $$$${daily}\:{pay}\:{back}:\:{D} \\ $$$${after}\:{t}\:{days}\:{the}\:{Youngs}\:{owe}\:{the}\:{bank} \\ $$$${money}\:{x}. \\ $$$$ \\ $$$${t}\:{as}\:{discrete}\:{variable}: \\ $$$${from}\:{Q}\mathrm{165404}\:{we}\:{have} \\ $$$${x}={Z}\left(\mathrm{1}+{r}\right)^{{t}} −\frac{{D}\left[\left(\mathrm{1}+{r}\right)^{{t}} −\mathrm{1}\right]}{{r}} \\ $$$${x}=\frac{{D}}{{r}}+\left({Z}−\frac{{D}}{{r}}\right)\left(\mathrm{1}+{r}\right)^{{t}} \\ $$
Commented by mr W last updated on 08/Feb/22
$${loan}:\:{Z} \\ $$$${daily}\:{interest}\:{rate}:\:{r} \\ $$$${daily}\:{pay}\:{back}:\:{D} \\ $$$${after}\:{t}\:{days}\:{the}\:{Youngs}\:{owe}\:{the}\:{bank} \\ $$$${money}\:{x}. \\ $$$$ \\ $$$${t}\:{as}\:{continous}\:{variable}: \\ $$$${dx}=\left({rx}−{D}\right){dt} \\ $$$$\frac{{dx}}{{dt}}={rx}−{D}\:\:\:\leftarrow\:{differential}\:{eqn}. \\ $$$$\frac{{dx}}{{rx}−{D}}={dt} \\ $$$$\mathrm{ln}\:\left({rx}−{D}\right)={rt}+{C}_{\mathrm{1}} \\ $$$$\Rightarrow{x}=\frac{{D}}{{r}}+{Ce}^{{rt}} \\ $$$${at}\:{t}=\mathrm{0}: \\ $$$$\Rightarrow{Z}=\frac{{D}}{{r}}+{C} \\ $$$$\Rightarrow{x}=\frac{{D}}{{r}}+\left({Z}−\frac{{D}}{{r}}\right){e}^{{rt}} \\ $$
Commented by MWSuSon last updated on 08/Feb/22
Thank you sir, you have been of wonderful help. i wish you success in all you do sir, thank you.
Commented by mr W last updated on 09/Feb/22
![thanks sir! this example shows exactly how the number “e” was discovered. when we calculate the interest not daily, e.g. we divide a day into many parts, then we get x=(D/r)+(Z−(D/r))(1+(r/n))^(nt) x=(D/r)+(Z−(D/r))[(1+(r/n))^(n/r) ]^(rt) when we divide a day into infinite many parts, i.e. n→∞, then x=(D/r)+(Z−(D/r))[lim_(n→∞) (1+(r/n))^(n/r) ]^(rt) people found that this number lim_(n→∞) (1+(r/n))^(n/r) really exists, and denoted it as “e”. and we get x=(D/r)+(Z−(D/r))e^(rt)](Q165846.png)
$${thanks}\:{sir}! \\ $$$${this}\:{example}\:{shows}\:{exactly}\:{how}\:{the} \\ $$$${number}\:``{e}''\:{was}\:{discovered}.\:{when} \\ $$$${we}\:{calculate}\:{the}\:{interest}\:{not}\:{daily}, \\ $$$${e}.{g}.\:{we}\:{divide}\:{a}\:{day}\:{into}\:{many}\:{parts}, \\ $$$${then}\:{we}\:{get} \\ $$$${x}=\frac{{D}}{{r}}+\left({Z}−\frac{{D}}{{r}}\right)\left(\mathrm{1}+\frac{{r}}{{n}}\right)^{{nt}} \\ $$$${x}=\frac{{D}}{{r}}+\left({Z}−\frac{{D}}{{r}}\right)\left[\left(\mathrm{1}+\frac{{r}}{{n}}\right)^{\frac{{n}}{{r}}} \right]^{{rt}} \\ $$$${when}\:{we}\:{divide}\:{a}\:{day}\:{into}\:{infinite} \\ $$$${many}\:{parts},\:{i}.{e}.\:{n}\rightarrow\infty,\:{then} \\ $$$${x}=\frac{{D}}{{r}}+\left({Z}−\frac{{D}}{{r}}\right)\left[\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{r}}{{n}}\right)^{\frac{{n}}{{r}}} \right]^{{rt}} \\ $$$${people}\:{found}\:{that}\:{this}\:{number} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{{r}}{{n}}\right)^{\frac{{n}}{{r}}} \:{really}\:{exists},\:{and} \\ $$$${denoted}\:{it}\:{as}\:``{e}''.\:{and}\:{we}\:{get} \\ $$$${x}=\frac{{D}}{{r}}+\left({Z}−\frac{{D}}{{r}}\right){e}^{{rt}} \\ $$
Commented by MWSuSon last updated on 09/Feb/22
I don't know why I don't get notified whenever there's a reply on my post, thank you sir for this additional info.
Commented by Tawa11 last updated on 10/Feb/22
$$\mathrm{Weldone}\:\mathrm{sir} \\ $$