Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 165879 by ajfour last updated on 09/Feb/22

	Answered by mr W last updated on 09/Feb/22

	Commented by ajfour last updated on 09/Feb/22
	Go ahead sir, i shall also try, n past two questions, extreme thanks to their solutions. Unbelievable presentation.I shall scrutinize them well, for sure.
	Commented by mr W last updated on 10/Feb/22

	$\tan 22.5 ° = \sqrt{2} - 1$ $\sin 22.5 ° = \frac{\sqrt{2} - 1}{\sqrt{4 - 2 \sqrt{2}}}$ $l e t t = \frac{1}{\tan 22.5 °} = \sqrt{2} + 1$ $l e t s = \frac{1}{\sin 22.5 °} = (\sqrt{2} + 1) \sqrt{2 (2 - \sqrt{2})}$ $O B = O C = O A = \frac{1}{\tan 22.5 °}$ $O K = O H = D H + O D = 1 + \frac{1}{\sin 22.5 °}$ $J B = \frac{1}{\tan 22.5 °} - R$ ${(\frac{1}{\tan 22.5 °} - R)}^{2} = {(1 + R)}^{2} - {(1 - R)}^{2}$ $R^{2} - 2 (t + 2) R + t^{2} = 0$ $\Rightarrow R = t + 2 - 2 \sqrt{t + 1}$ $C E = O K - O C - E K = 1 + \frac{1}{\sin 22.5 °} - \frac{1}{\tan 22.5 °} - r$ ${(r + 1)}^{2} = 1^{2} + {(1 + \frac{1}{\sin 22.5 °} - \frac{1}{\tan 22.5 °} - r)}^{2}$ ${(1 + s - t)}^{2} = 2 (2 + s - t) r$ $\Rightarrow r = \frac{{(1 + s - t)}^{2}}{2 (2 + s - t)}$ $\frac{R}{r} = \frac{2 (2 + s - t) (2 + t - 2 \sqrt{t + 1})}{{(1 + s - t)}^{2}} \approx 2.1989$
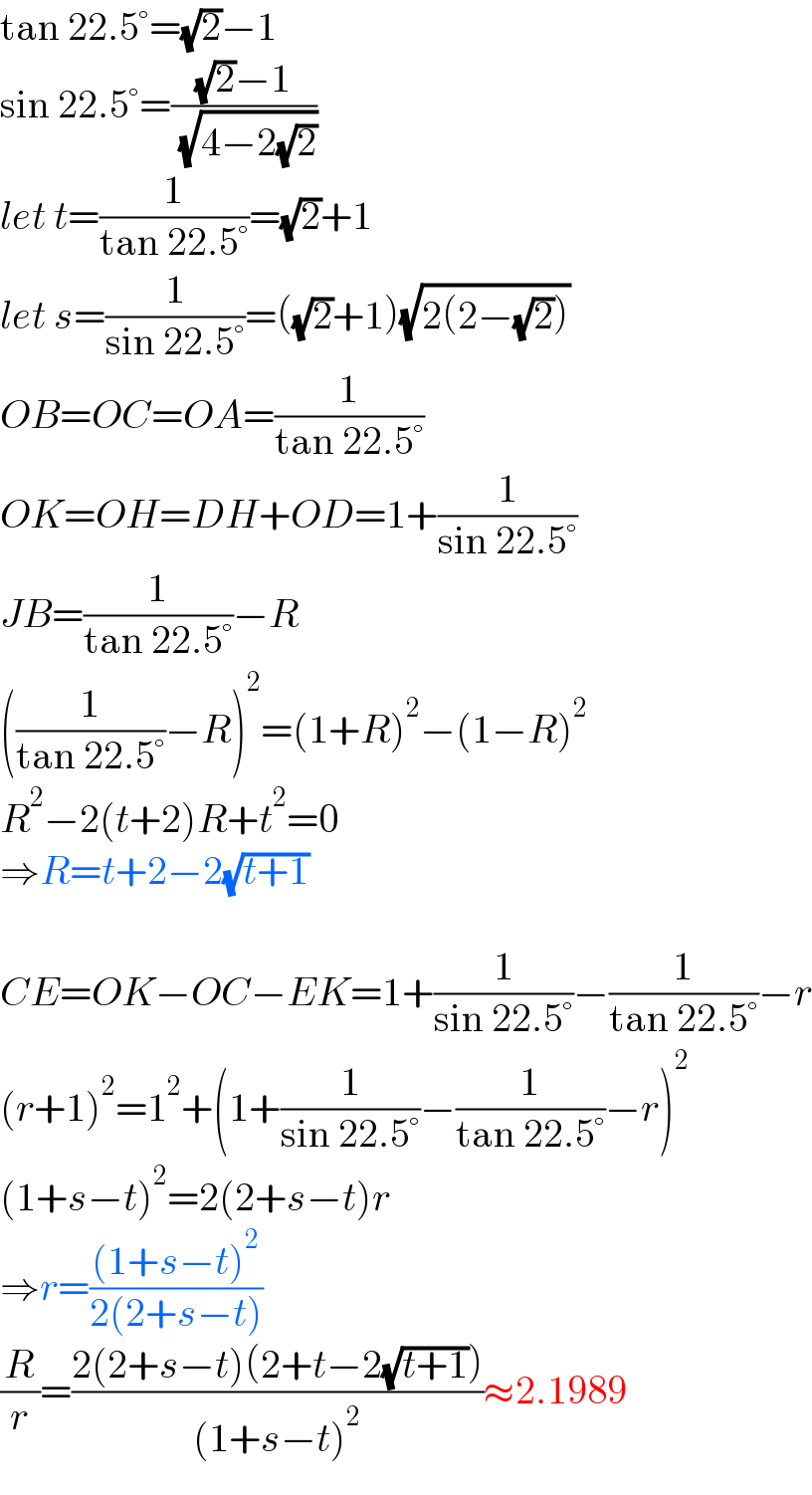
	Commented by mr W last updated on 09/Feb/22

	Commented by MJS_new last updated on 10/Feb/22

	$great! the solution can be simplified :$ $\frac{R}{r} = 1 - \sqrt{2} + \sqrt{2 (2 + \sqrt{2})}$
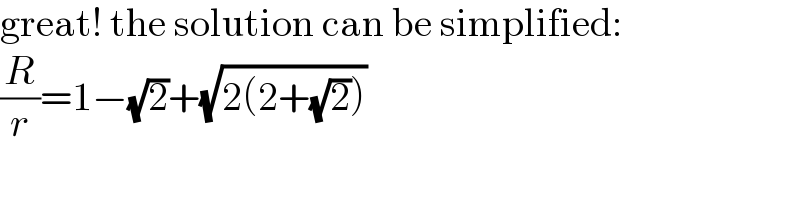
	Commented by ajfour last updated on 09/Feb/22

	$A w e s o m e s o l u t i o n s i r .$
	Commented by mr W last updated on 10/Feb/22

	$t h a n k s s i r s!$
	Commented by Tawa11 last updated on 10/Feb/22

	$Weldone sir .$
	Answered by ajfour last updated on 09/Feb/22

	Commented by ajfour last updated on 10/Feb/22
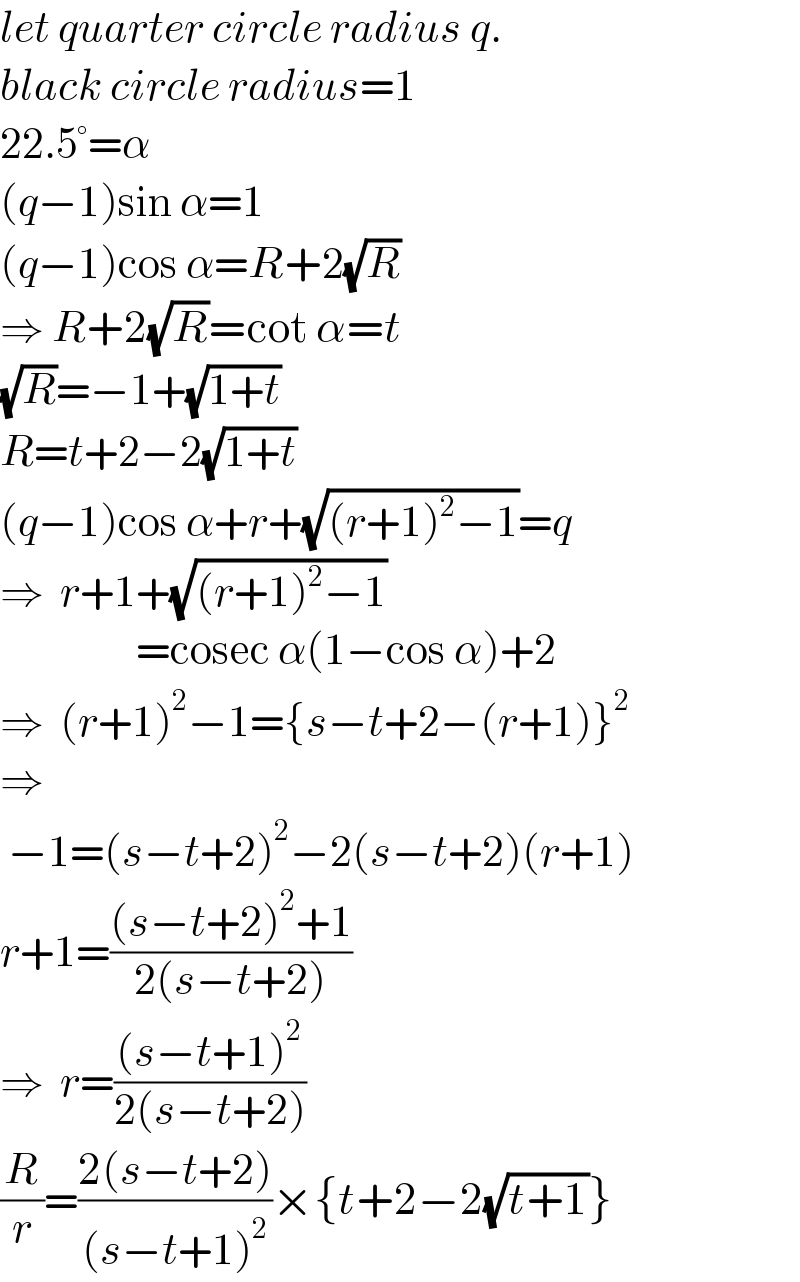
	$let quarter circle radius q. black circle radius=1 22.5°=α (q−1)sin α=1 (q−1)cos α=R+2(√R) ⇒ R+2(√R)=cot α=t (√R)=−1+(√(1+t)) R=t+2−2(√(1+t)) (q−1)cos α+r+(√((r+1)^2 −1))=q ⇒ r+1+(√((r+1)^2 −1)) =cosec α(1−cos α)+2 ⇒ (r+1)^2 −1={s−t+2−(r+1)}^2 ⇒ −1=(s−t+2)^2 −2(s−t+2)(r+1) r+1=(((s−t+2)^2 +1)/(2(s−t+2))) ⇒ r=(((s−t+1)^2 )/(2(s−t+2))) (R/r)=((2(s−t+2))/((s−t+1)^2 ))×{t+2−2(√(t+1))}$
	$l e t q u a r t e r c i r c l e r a d i u s q .$ $b l a c k c i r c l e r a d i u s = 1$ $22.5 ° = α$ $(q - 1) \sin α = 1$ $(q - 1) \cos α = R + 2 \sqrt{R}$ $\Rightarrow R + 2 \sqrt{R} = \cot α = t$ $\sqrt{R} = - 1 + \sqrt{1 + t}$ $R = t + 2 - 2 \sqrt{1 + t}$ $(q - 1) \cos α + r + \sqrt{{(r + 1)}^{2} - 1} = q$ $\Rightarrow r + 1 + \sqrt{{(r + 1)}^{2} - 1}$ $= cosec α (1 - \cos α) + 2$ $\Rightarrow {(r + 1)}^{2} - 1 = {s - t + 2 - (r + 1)}^{2}$ $\Rightarrow$ $- 1 = {(s - t + 2)}^{2} - 2 (s - t + 2) (r + 1)$ $r + 1 = \frac{{(s - t + 2)}^{2} + 1}{2 (s - t + 2)}$ $\Rightarrow r = \frac{{(s - t + 1)}^{2}}{2 (s - t + 2)}$ $\frac{R}{r} = \frac{2 (s - t + 2)}{{(s - t + 1)}^{2}} \times {t + 2 - 2 \sqrt{t + 1}}$
	Commented by Tawa11 last updated on 10/Feb/22

	$Weldone sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum