Question Number 166141 by Lambert last updated on 13/Feb/22
$$\int_{\mathrm{0}} ^{\boldsymbol{\mathrm{x}}} \frac{\boldsymbol{\mathrm{t}}^{\mathrm{2}} }{\:\sqrt{\boldsymbol{\mathrm{a}}+\mathrm{2}\boldsymbol{\mathrm{t}}^{\mathrm{2}} }}\boldsymbol{\mathrm{dt}}\: \\ $$
Answered by MJS_new last updated on 14/Feb/22
![∫(t^2 /( (√(a+2t^2 ))))dt= [u=((√2)/( (√a)))(t+(√(a+2t^2 ))) → dt=((√(a+2t^2 ))/( (√2)u))du] =((a(√2))/(16))∫(((u^2 −1)^2 )/u^3 )du=((a(√2))/(16))∫(u−(2/u)+(1/u^3 ))du= =((a(√2))/(16))((u^2 /2)−2ln u −(1/(2u^2 )))=... =((t(√(a+2t^2 )))/4)−((a(√2))/8)ln ((√2)t+(√(a+2t^2 ))) +C the rest is easy](Q166148.png)
$$\int\frac{{t}^{\mathrm{2}} }{\:\sqrt{{a}+\mathrm{2}{t}^{\mathrm{2}} }}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{{a}}}\left({t}+\sqrt{{a}+\mathrm{2}{t}^{\mathrm{2}} }\right)\:\rightarrow\:{dt}=\frac{\sqrt{{a}+\mathrm{2}{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}{u}}{du}\right] \\ $$$$=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{16}}\int\frac{\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{3}} }{du}=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{16}}\int\left({u}−\frac{\mathrm{2}}{{u}}+\frac{\mathrm{1}}{{u}^{\mathrm{3}} }\right){du}= \\ $$$$=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{16}}\left(\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2ln}\:{u}\:−\frac{\mathrm{1}}{\mathrm{2}{u}^{\mathrm{2}} }\right)=... \\ $$$$=\frac{{t}\sqrt{{a}+\mathrm{2}{t}^{\mathrm{2}} }}{\mathrm{4}}−\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}{t}+\sqrt{{a}+\mathrm{2}{t}^{\mathrm{2}} }\right)\:+{C} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by cortano1 last updated on 14/Feb/22
$$\:\mathrm{u}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{a}}}\:\mathrm{t}?\:\mathrm{sir} \\ $$
Commented by MJS_new last updated on 14/Feb/22
$$\mathrm{typo}\:=\:\mathrm{instead}\:\mathrm{of}\:+;\:\mathrm{it}'\mathrm{s}\:\mathrm{now}\:\mathrm{corrected} \\ $$
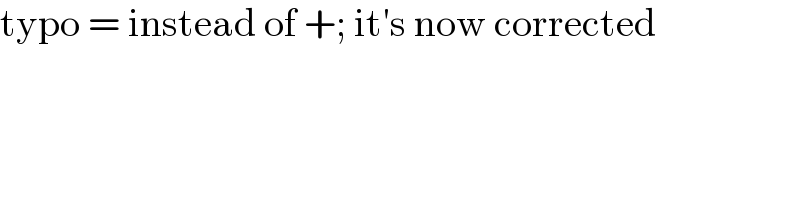
Answered by Mathspace last updated on 14/Feb/22
![f(a)=(1/( (√a)))∫_0 ^x (t^2 /( (√(1+((2t^2 )/a)))))dt =(a/2)×(1/( (√a)))∫_0 ^x (((2/a)t^2 )/( (√(1+((2t^2 )/a)))))dt =((√a)/2)∫_0 ^x (√(1+((2t^2 )/a)))dt−((√a)/2)∫_0 ^x (dt/( (√(1+((2t^2 )/a))))) (((√2)t)/( (√a)))=shu ⇒u=argsh((((√2)t)/( (√a)))) ∫_0 ^x (√(1+((2t^2 )/a)))dt=∫_0 ^(argsh((((√2)x)/( (√a))))) chu.((√a)/( (√2)))chudu =((√a)/( (√2)))∫_0 ^(ln((((√2)x)/( (√a)))+(√(1+((2x^2 )/a))))) ((1+ch(2u))/2)du =((√a)/2)ln(....)+((√a)/(4(√2)))[sh(2u)]_0 ^(ln(...)) =((√a)/2)ln(...)+((√a)/(4(√2)))[((e^(2u) −e^(−2u) )/2)]_0 ^(ln(...)) =((√a)/2)ln((((√2)x)/( (√a)))+(√(1+((2x^2 )/a)))) ((√a)/(8(√2))){ ((((√2)x)/( (√a)))+(√(1+((2x^2 )/a))))^2 −((((√2)x)/( (√a)))+(√(1+((2x^2 )/a))))^(−2) } same way for other integral...](Q166155.png)
$${f}\left({a}\right)=\frac{\mathrm{1}}{\:\sqrt{{a}}}\int_{\mathrm{0}} ^{{x}} \:\frac{{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\frac{\mathrm{2}{t}^{\mathrm{2}} }{{a}}}}{dt} \\ $$$$=\frac{{a}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{{a}}}\int_{\mathrm{0}} ^{{x}} \:\frac{\frac{\mathrm{2}}{{a}}{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\frac{\mathrm{2}{t}^{\mathrm{2}} }{{a}}}}{dt} \\ $$$$=\frac{\sqrt{{a}}}{\mathrm{2}}\int_{\mathrm{0}} ^{{x}} \sqrt{\mathrm{1}+\frac{\mathrm{2}{t}^{\mathrm{2}} }{{a}}}{dt}−\frac{\sqrt{{a}}}{\mathrm{2}}\int_{\mathrm{0}} ^{{x}} \frac{{dt}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{2}{t}^{\mathrm{2}} }{{a}}}} \\ $$$$\frac{\sqrt{\mathrm{2}}{t}}{\:\sqrt{{a}}}={shu}\:\Rightarrow{u}={argsh}\left(\frac{\sqrt{\mathrm{2}}{t}}{\:\sqrt{{a}}}\right) \\ $$$$\int_{\mathrm{0}} ^{{x}} \sqrt{\mathrm{1}+\frac{\mathrm{2}{t}^{\mathrm{2}} }{{a}}}{dt}=\int_{\mathrm{0}} ^{{argsh}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{{a}}}\right)} {chu}.\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}{chudu} \\ $$$$=\frac{\sqrt{{a}}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{{ln}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{{a}}}+\sqrt{\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} }{{a}}}\right)} \:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}}{du} \\ $$$$=\frac{\sqrt{{a}}}{\mathrm{2}}{ln}\left(....\right)+\frac{\sqrt{{a}}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[{sh}\left(\mathrm{2}{u}\right)\right]_{\mathrm{0}} ^{{ln}\left(...\right)} \\ $$$$=\frac{\sqrt{{a}}}{\mathrm{2}}{ln}\left(...\right)+\frac{\sqrt{{a}}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{{ln}\left(...\right)} \\ $$$$=\frac{\sqrt{{a}}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{{a}}}+\sqrt{\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} }{{a}}}\right) \\ $$$$\frac{\sqrt{{a}}}{\mathrm{8}\sqrt{\mathrm{2}}}\left\{\:\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{{a}}}+\sqrt{\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} }{{a}}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{{a}}}+\sqrt{\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{2}} }{{a}}}\right)^{−\mathrm{2}} \right\} \\ $$$${same}\:{way}\:{for}\:{other}\:{integral}... \\ $$