Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 166301 by LEKOUMA last updated on 18/Feb/22

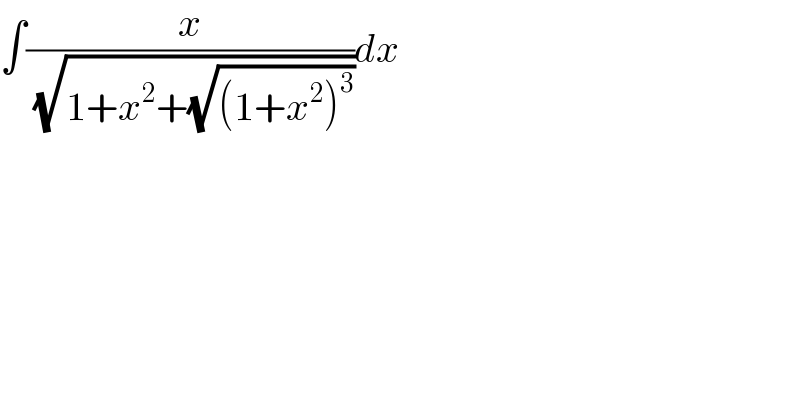
∫(x/( (√(1+x^2 +(√((1+x^2 )^3 ))))))dx

$$\int\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}}{dx} \\ $$

Answered by MJS_new last updated on 18/Feb/22

∫(x/( (√(x^2 +1+(x^2 +1)^(3/2) ))))dx= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))dt] =((√2)/2)∫((t−1)/t^(3/2) )dt=((√2)/2)(2t^(1/2) +(2/t^(1/2) ))=(((√2)(t+1))/( (√t)))= ... =2(√(1+(√(x^2 +1))))+C

$$\int\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}+\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dt}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}−\mathrm{1}}{{t}^{\mathrm{3}/\mathrm{2}} }{dt}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{2}{t}^{\mathrm{1}/\mathrm{2}} +\frac{\mathrm{2}}{{t}^{\mathrm{1}/\mathrm{2}} }\right)=\frac{\sqrt{\mathrm{2}}\left({t}+\mathrm{1}\right)}{\:\sqrt{{t}}}= \\ $$$$... \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+{C} \\ $$

Commented by cortano1 last updated on 18/Feb/22

Euler subtitution

$$\mathrm{Euler}\:\mathrm{subtitution} \\ $$

Commented by peter frank last updated on 19/Feb/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by cortano1 last updated on 18/Feb/22

∫ (1/( (√(1+x^2 +(√((1+x^2 )^3 )))))) (x dx) let y=(√(1+x^2 )) ⇒y^2 =1+x^2 ⇒y dy = x dx I=∫ ((y dy)/( (√(y^2 +y^3 )))) = ∫ (dy/( (√(1+y)))) I=∫ (1+y)^(−(1/2)) dy = 2(√(1+y)) + c I=2(√(1+(√(1+x^2 )))) + c

$$\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\sqrt{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}}\:\left(\mathrm{x}\:\mathrm{dx}\right) \\ $$$$\:\mathrm{let}\:\mathrm{y}=\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{y}^{\mathrm{2}} =\mathrm{1}+\mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}\:\mathrm{dy}\:=\:\mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{y}\:\mathrm{dy}}{\:\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{y}^{\mathrm{3}} }}\:=\:\int\:\frac{\mathrm{dy}}{\:\sqrt{\mathrm{1}+\mathrm{y}}} \\ $$$$\mathrm{I}=\int\:\left(\mathrm{1}+\mathrm{y}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dy}\:=\:\mathrm{2}\sqrt{\mathrm{1}+\mathrm{y}}\:+\:\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{2}\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:+\:\mathrm{c}\: \\ $$

Commented by LEKOUMA last updated on 18/Feb/22

Thanks

$${Thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com