
Question and Answers Forum
Question Number 166320 by bobhans last updated on 18/Feb/22
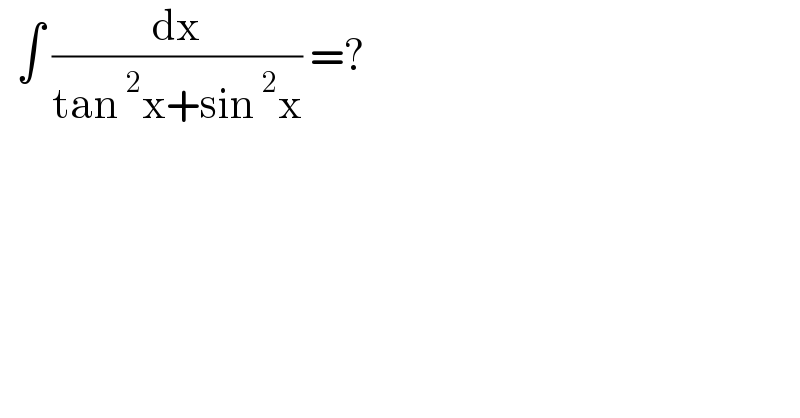
Answered by cortano1 last updated on 18/Feb/22
![Y=∫ (dx/(tan^2 x+sin^2 x)) =? Y=∫ ((sec^2 x)/(sec^2 x(tan^2 x+sin^2 x))) dx Y=∫ ((sec^2 x)/(sec^2 x tan^2 x+tan^2 x)) dx Y=∫ ((sec^2 x)/(tan^2 x(sec^2 x+1))) dx Y= ∫((d(tan x))/(tan^2 x(2+tan^2 x))) Y= ∫ (dy/(y^2 (2+y^2 ))) ; [ y=tan x ] Y=∫ (1/2)((1/y^2 )−(1/(2+y^2 )))dy Y=(1/2)∫(y^(−2) −(1/(((√2))^2 +y^2 )))dy Y=−(1/(2y))−(1/2).(1/( (√2)))arctan ((y/( (√2))))+c Y=−(1/(2tan x))−((√2)/4)arctan (((tan x)/( (√2))))+ c](Q166322.png)
Commented by peter frank last updated on 19/Feb/22

| ||
Question and Answers Forum | ||
Question Number 166320 by bobhans last updated on 18/Feb/22 | ||
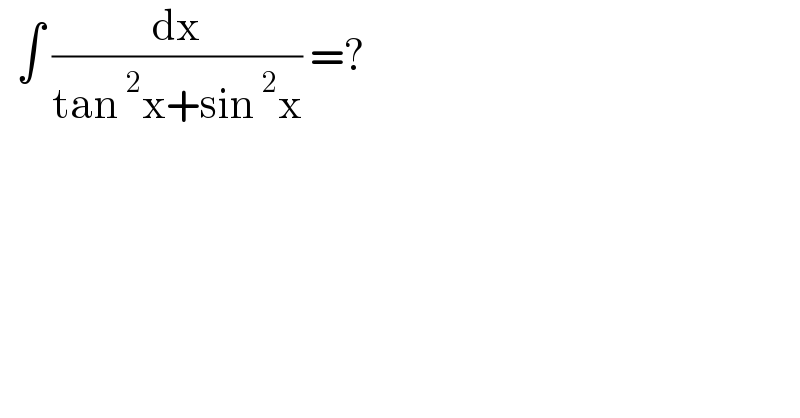 | ||
Answered by cortano1 last updated on 18/Feb/22 | ||
![Y=∫ (dx/(tan^2 x+sin^2 x)) =? Y=∫ ((sec^2 x)/(sec^2 x(tan^2 x+sin^2 x))) dx Y=∫ ((sec^2 x)/(sec^2 x tan^2 x+tan^2 x)) dx Y=∫ ((sec^2 x)/(tan^2 x(sec^2 x+1))) dx Y= ∫((d(tan x))/(tan^2 x(2+tan^2 x))) Y= ∫ (dy/(y^2 (2+y^2 ))) ; [ y=tan x ] Y=∫ (1/2)((1/y^2 )−(1/(2+y^2 )))dy Y=(1/2)∫(y^(−2) −(1/(((√2))^2 +y^2 )))dy Y=−(1/(2y))−(1/2).(1/( (√2)))arctan ((y/( (√2))))+c Y=−(1/(2tan x))−((√2)/4)arctan (((tan x)/( (√2))))+ c](Q166322.png) | ||
| ||
Commented by peter frank last updated on 19/Feb/22 | ||
 | ||