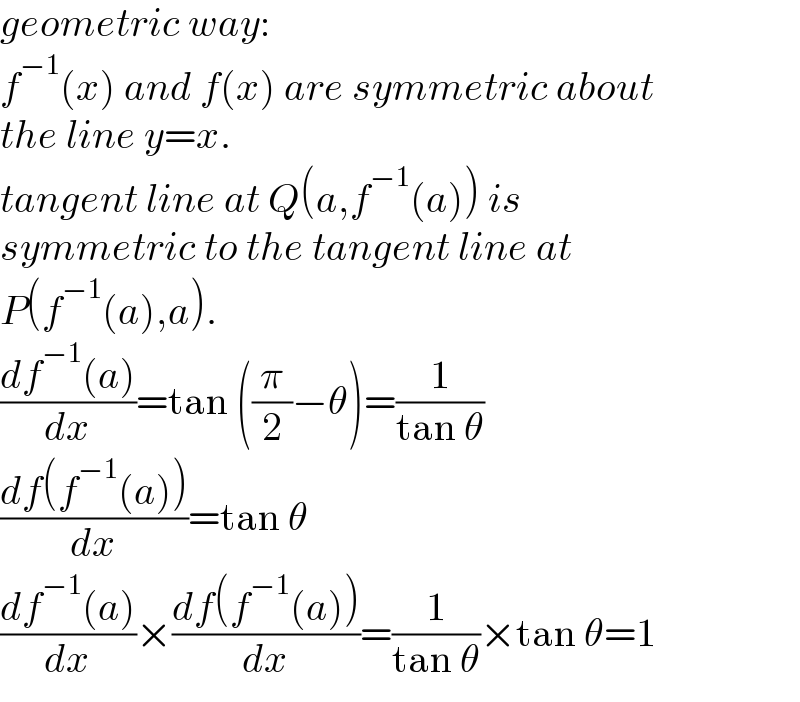Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 166331 by mr W last updated on 18/Feb/22

$$provethat$$$$\frac{{df}^{-1}\left(a\right)}{dx}\times \frac{df\left(f^{-1}\left(a\right)\right)}{dx}=1$$

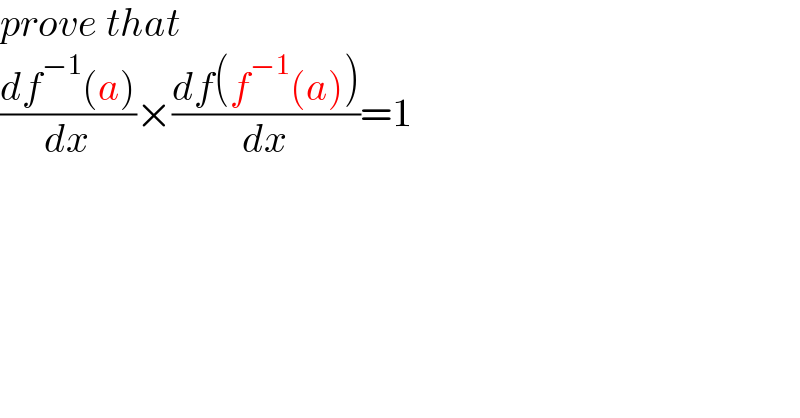
Commented by mr W last updated on 19/Feb/22

$$itismeantthat$$$$\frac{{df}^{-1}\left(a\right)}{dx}=\frac{{df}^{-1}\left(x\right)}{dx}{\mid }_{x=a}$$$$\frac{df\left(f^{-1}\left(a\right)\right)}{dx}=\frac{df\left(x\right)}{dx}{\mid }_{x=f^{-1}\left(a\right)}$$

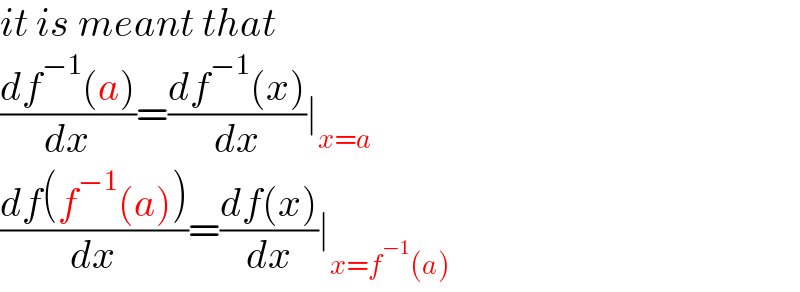
Answered by mathsmine last updated on 18/Feb/22

$${fof}^{-}\left(x\right)=x$$$$\Rightarrow \frac{{df}^{-}\left(x\right)}{dx}.\frac{df}{dx}\left(f^{-}\left(x\right)\right)=1$$$$x=a$$

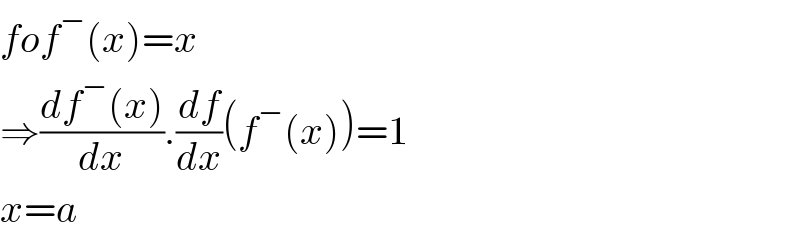
Commented by mr W last updated on 18/Feb/22

$$thankssir!$$

Answered by mr W last updated on 19/Feb/22

Commented by mr W last updated on 18/Feb/22

$$geometricway:$$$$f^{-1}\left(x\right)andf\left(x\right)aresymmetricabout$$$$theliney=x.$$$$tangentlineatQ(a,f^{-1}\left(a\right))is$$$$symmetrictothetangentlineat$$$$P(f^{-1}\left(a\right),a).$$$$\frac{{df}^{-1}\left(a\right)}{dx}=\tan (\frac{\pi }{2}-\theta )=\frac{1}{\tan \theta }$$$$\frac{df\left(f^{-1}\left(a\right)\right)}{dx}=\tan \theta$$$$\frac{{df}^{-1}\left(a\right)}{dx}\times \frac{df\left(f^{-1}\left(a\right)\right)}{dx}=\frac{1}{\tan \theta }\times \tan \theta =1$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com