Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 166417 by ajfour last updated on 19/Feb/22

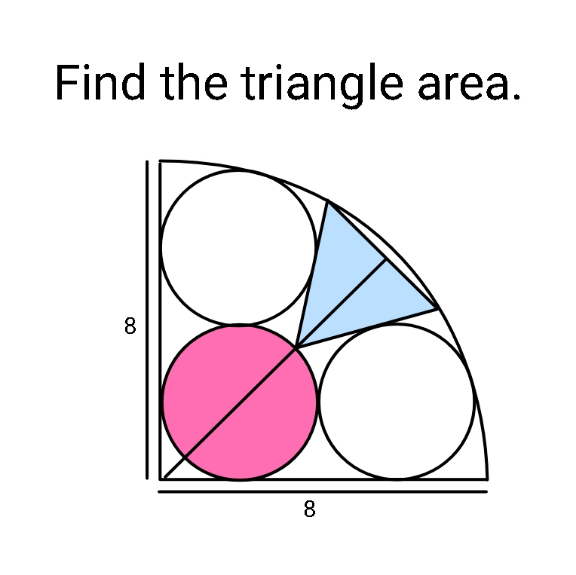
	Answered by mr W last updated on 20/Feb/22

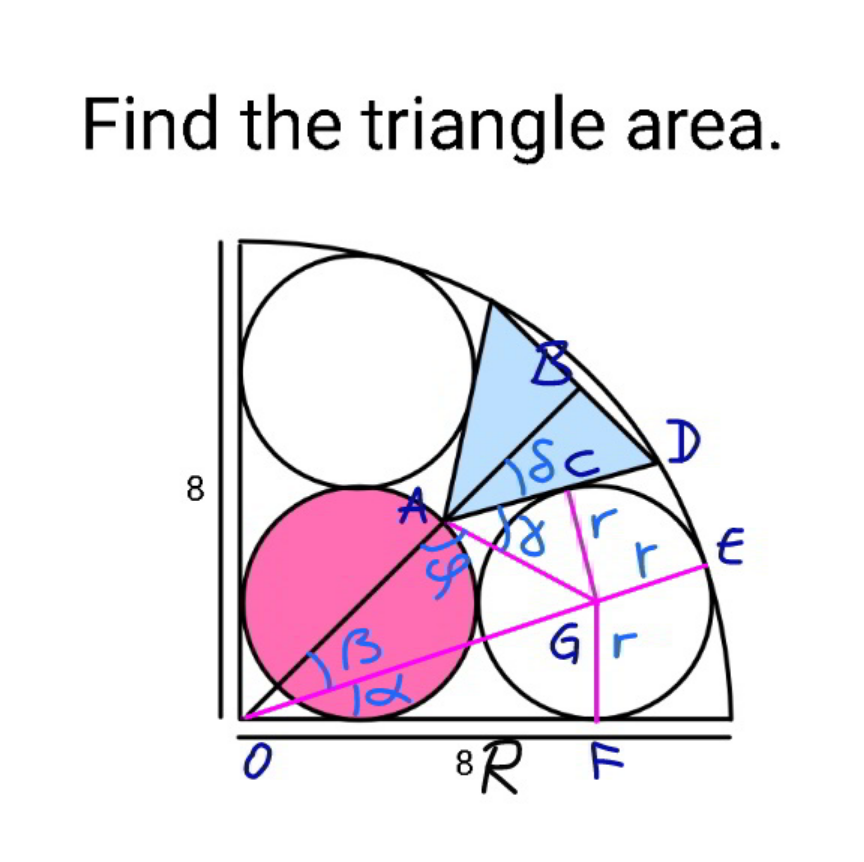
	Commented by mr W last updated on 20/Feb/22

	$O G = R - r$ $O F = 3 r$ ${(R - r)}^{2} = {(3 r)}^{2} + r^{2}$ $9 r^{2} + 2 R r - R^{2} = 0$ $\Rightarrow r = \frac{(\sqrt{10} - 1) R}{9}$ $\tan α = \frac{1}{3} \Rightarrow α = \tan^{- 1} \frac{1}{3}$ $β = \frac{π}{4} - α$ $O A = (1 + \sqrt{2}) r$ ${A G}^{2} = {(1 + \sqrt{2})}^{2} r^{2} + {(\sqrt{10} r)}^{2} - 2 (1 + \sqrt{2}) \sqrt{10} r^{2} \cos β$ ${A G}^{2} = (13 + 2 \sqrt{2} - 2 (1 + \sqrt{2}) \sqrt{10} \frac{1}{\sqrt{2}} (\frac{3}{\sqrt{10}} + \frac{1}{\sqrt{10}})) r^{2}$ ${A G}^{2} = (5 - 2 \sqrt{2}) r^{2}$ $A G = \sqrt{5 - 2 \sqrt{2}} r ✓$ $\frac{\sin φ}{\sqrt{10} r} = \frac{\sin β}{\sqrt{5 - 2 \sqrt{2}} r}$ $\sin φ = \frac{\sqrt{10}}{\sqrt{5 - 2 \sqrt{2}}} \times \frac{1}{\sqrt{2}} (\frac{3}{\sqrt{10}} - \frac{1}{\sqrt{10}})$ $\sin φ = \frac{\sqrt{2}}{\sqrt{5 - 2 \sqrt{2}}} \Rightarrow φ = π - \sin^{- 1} \frac{\sqrt{2}}{\sqrt{5 - 2 \sqrt{2}}}$ $\sin γ = \frac{1}{\sqrt{5 - 2 \sqrt{2}}} \Rightarrow γ = \sin^{- 1} \frac{1}{\sqrt{5 - 2 \sqrt{2}}}$ $δ = π - φ - γ = \sin^{- 1} \frac{\sqrt{2}}{\sqrt{5 - 2 \sqrt{2}}} - \sin^{- 1} \frac{1}{\sqrt{5 - 2 \sqrt{2}}}$ $\cos δ = \frac{\sqrt{(5 - 2 \sqrt{2} - 2) (5 - 2 \sqrt{2} - 1)}}{5 - 2 \sqrt{2}} + \frac{\sqrt{2}}{5 - 2 \sqrt{2}}$ $\cos δ = \frac{\sqrt{2} (1 + \sqrt{10 - 7 \sqrt{2}})}{5 - 2 \sqrt{2}}$ $\sin δ = \frac{\sqrt{2 (5 - 2 \sqrt{2} - 1)} - \sqrt{5 - 2 \sqrt{2} - 2}}{5 - 2 \sqrt{2}}$ $\sin δ = \frac{2 \sqrt{2 - \sqrt{2}} + 1 - \sqrt{2}}{5 - 2 \sqrt{2}}$ $O B = (1 + \sqrt{2}) r + A D \cos δ$ $B D = A D \sin δ$ ${O B}^{2} + {B D}^{2} = {O D}^{2} = R^{2}$ ${[(1 + \sqrt{2}) r + A D \cos δ]}^{2} + {(A D \sin δ)}^{2} = R^{2}$ ${(A D)}^{2} + 2 (1 + \sqrt{2}) \cos δ A D + {(1 + \sqrt{2})}^{2} - R^{2} = 0$ ${(\frac{A D}{r})}^{2} + 2 (1 + \sqrt{2}) \cos δ (\frac{A D}{r}) + {(1 + \sqrt{2})}^{2} - {(\frac{9}{\sqrt{10} - 1})}^{2} = 0$ ${(\frac{A D}{r})}^{2} + 2 (1 + \sqrt{2}) \frac{\sqrt{2} (1 + \sqrt{10 - 7 \sqrt{2}})}{5 - 2 \sqrt{2}} (\frac{A D}{r}) + {(1 + \sqrt{2})}^{2} - {(\frac{9}{\sqrt{10} - 1})}^{2} = 0$ ${(\frac{A D}{r})}^{2} + \frac{2 (14 + 9 \sqrt{2}) (1 + \sqrt{10 - 7 \sqrt{2}})}{17} (\frac{A D}{r}) - 2 (4 + \sqrt{10} - \sqrt{2}) = 0$ $\frac{A D}{r} = - \frac{(14 + 9 \sqrt{2}) (1 + \sqrt{10 - 7 \sqrt{2}})}{17} + \sqrt{\frac{{(14 + 9 \sqrt{2})}^{2} {(1 + \sqrt{10 - 7 \sqrt{2}})}^{2}}{17^{2}} + 2 (4 + \sqrt{10} - \sqrt{2})}$ $\frac{A D}{r} = \frac{\sqrt{2722 + 578 \sqrt{10} - 312 \sqrt{2} + (716 + 504 \sqrt{2}) \sqrt{10 - 7 \sqrt{2}}} - (14 + 9 \sqrt{2}) (1 + \sqrt{10 - 7 \sqrt{2}})}{17}$ $A r e a o f t r i a n g l e$ $A = {(A D)}^{2} \sin δ \cos δ$ $\approx 1.5956802 r^{2}$ $\approx 0.0921051 R^{2}$ $\approx 5.8947276$
	Commented by Tawa11 last updated on 20/Feb/22

	$Great sir .$
	Commented by ajfour last updated on 20/Feb/22
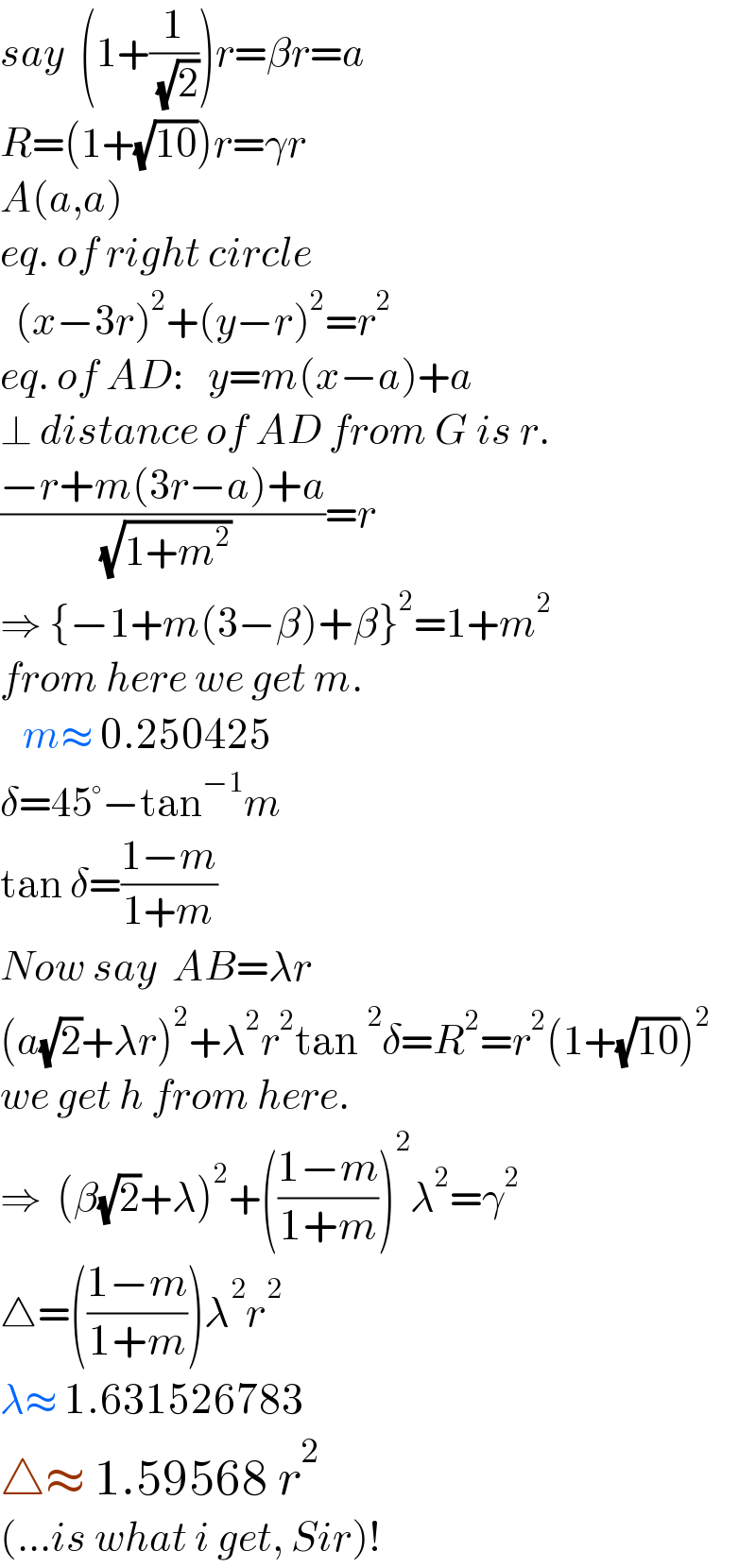
	$say (1+(1/( (√2))))r=βr=a R=(1+(√(10)))r=γr A(a,a) eq. of right circle (x−3r)^2 +(y−r)^2 =r^2 eq. of AD: y=m(x−a)+a ⊥ distance of AD from G is r. ((−r+m(3r−a)+a)/( (√(1+m^2 ))))=r ⇒ {−1+m(3−β)+β}^2 =1+m^2 from here we get m. m≈ 0.250425 δ=45°−tan^(−1) m tan δ=((1−m)/(1+m)) Now say AB=λr (a(√2)+λr)^2 +λ^2 r^2 tan^2 δ=R^2 =r^2 (1+(√(10)))^2 we get h from here. ⇒ (β(√2)+λ)^2 +(((1−m)/(1+m)))^2 λ^2 =γ^2 △=(((1−m)/(1+m)))λ^2 r^2 λ≈ 1.631526783 △≈ 1.59568 r^2 (...is what i get, Sir)!$
	$s a y (1 + \frac{1}{\sqrt{2}}) r = β r = a$ $R = (1 + \sqrt{10}) r = γ r$ $A (a, a)$ $e q . o f r i g h t c i r c l e$ ${(x - 3 r)}^{2} + {(y - r)}^{2} = r^{2}$ $e q . o f A D : y = m (x - a) + a$ $⊥ d i s t a n c e o f A D f r o m G i s r .$ $\frac{- r + m (3 r - a) + a}{\sqrt{1 + m^{2}}} = r$ $\Rightarrow {- 1 + m (3 - β) + β}^{2} = 1 + m^{2}$ $f r o m h e r e w e g e t m .$ $m \approx 0.250425$ $δ = 45 ° - \tan^{- 1} m$ $\tan δ = \frac{1 - m}{1 + m}$ $N o w s a y A B = λ r$ ${(a \sqrt{2} + λ r)}^{2} + λ^{2} r^{2} \tan^{2} δ = R^{2} = r^{2} {(1 + \sqrt{10})}^{2}$ $w e g e t h f r o m h e r e .$ $\Rightarrow {(β \sqrt{2} + λ)}^{2} + {(\frac{1 - m}{1 + m})}^{2} λ^{2} = γ^{2}$ $△ = (\frac{1 - m}{1 + m}) λ^{2} r^{2}$ $λ \approx 1.631526783$ $△ \approx 1.59568 r^{2}$ $(. . . i s w h a t i g e t, S i r)!$
	Commented by mr W last updated on 20/Feb/22

	$f i n e s i r!$ $c a n A \approx 1.5956802 r^{2} b e c o m f i r m e d ?$
	Commented by ajfour last updated on 20/Feb/22

	$y e a h, i t s a b s o l u t e l y c o n f i r m e d!$
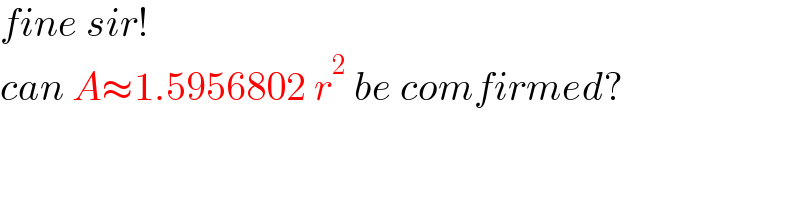
	Commented by ajfour last updated on 20/Feb/22
	Awesome solution sir.
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum