
Question Number 166627 by cortano1 last updated on 23/Feb/22
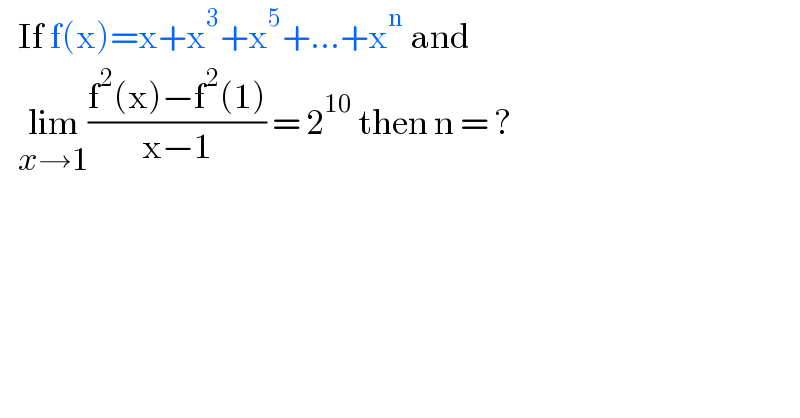
$$\:\:\:\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}+\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{5}} +...+\mathrm{x}^{\mathrm{n}} \:\mathrm{and}\: \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{f}^{\mathrm{2}} \left(\mathrm{1}\right)}{\mathrm{x}−\mathrm{1}}\:=\:\mathrm{2}^{\mathrm{10}} \:\mathrm{then}\:\mathrm{n}\:=\:? \\ $$
Commented by MJS_new last updated on 23/Feb/22

$$\mathrm{15} \\ $$
Commented by cortano1 last updated on 23/Feb/22

$$\mathrm{why}? \\ $$
Answered by MJS_new last updated on 23/Feb/22
![I took f^2 (x) = (f(x))^2 f(x)=x+x^3 +x^5 +...+x^(2k−1) ⇒ f(1)=k f(x)=Σ_(j=1) ^k x^(2j−1) =((x(x^(2k) −1))/(x^2 −1)); lim_(x→1) ((x(x^(2k) −1))/(x^2 −1)) =k ⇒ f(1)=k ((f^2 (x)−f^2 (1))/(x−1))=((x^(4k+2) −2x^(2k+2) −k^2 x^2 +x^2 −k^2 )/(x^5 −x^4 −2x^3 +2x^2 +x−1)) lim_(x→1) ((f^2 (x)−f^2 (1))/(x−1)) = =lim_(x→1) (((d^3 /dx^3 )[x^(4k+2) −2x^(2k+2) −k^2 x^2 +x^2 −k^2 ])/((d^3 /dx^3 )[x^5 −x^4 −2x^3 +2x^2 +x−1]))= =lim_(x→1) ((2kx((2k+1)(4k+1)x^(4k−2) −(k+1)(2k+1)x^(2k−2) −3kx))/(3(5x^2 −2x−1))) =2k^3 2k^3 =2^(10) k^3 =2^9 k=2^3 =8 n=2k−1=15](Q166632.png)
$$\mathrm{I}\:\mathrm{took}\:{f}^{\mathrm{2}} \left({x}\right)\:=\:\left({f}\left({x}\right)\right)^{\mathrm{2}} \\ $$$${f}\left({x}\right)={x}+{x}^{\mathrm{3}} +{x}^{\mathrm{5}} +...+{x}^{\mathrm{2}{k}−\mathrm{1}} \:\Rightarrow\:{f}\left(\mathrm{1}\right)={k} \\ $$$${f}\left({x}\right)=\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}{x}^{\mathrm{2}{j}−\mathrm{1}} =\frac{{x}\left({x}^{\mathrm{2}{k}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} −\mathrm{1}};\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}\left({x}^{\mathrm{2}{k}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}\:={k}\:\Rightarrow\:{f}\left(\mathrm{1}\right)={k} \\ $$$$\frac{{f}^{\mathrm{2}} \left({x}\right)−{f}^{\mathrm{2}} \left(\mathrm{1}\right)}{{x}−\mathrm{1}}=\frac{{x}^{\mathrm{4}{k}+\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}{k}+\mathrm{2}} −{k}^{\mathrm{2}} {x}^{\mathrm{2}} +{x}^{\mathrm{2}} −{k}^{\mathrm{2}} }{{x}^{\mathrm{5}} −{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{f}^{\mathrm{2}} \left({x}\right)−{f}^{\mathrm{2}} \left(\mathrm{1}\right)}{{x}−\mathrm{1}}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{{d}^{\mathrm{3}} }{{dx}^{\mathrm{3}} }\left[{x}^{\mathrm{4}{k}+\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}{k}+\mathrm{2}} −{k}^{\mathrm{2}} {x}^{\mathrm{2}} +{x}^{\mathrm{2}} −{k}^{\mathrm{2}} \right]}{\frac{{d}^{\mathrm{3}} }{{dx}^{\mathrm{3}} }\left[{x}^{\mathrm{5}} −{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{1}\right]}= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{2}{kx}\left(\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{4}{k}+\mathrm{1}\right){x}^{\mathrm{4}{k}−\mathrm{2}} −\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right){x}^{\mathrm{2}{k}−\mathrm{2}} −\mathrm{3}{kx}\right)}{\mathrm{3}\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)}\:=\mathrm{2}{k}^{\mathrm{3}} \\ $$$$\mathrm{2}{k}^{\mathrm{3}} =\mathrm{2}^{\mathrm{10}} \\ $$$${k}^{\mathrm{3}} =\mathrm{2}^{\mathrm{9}} \\ $$$${k}=\mathrm{2}^{\mathrm{3}} =\mathrm{8} \\ $$$${n}=\mathrm{2}{k}−\mathrm{1}=\mathrm{15} \\ $$
Commented by cortano1 last updated on 24/Feb/22
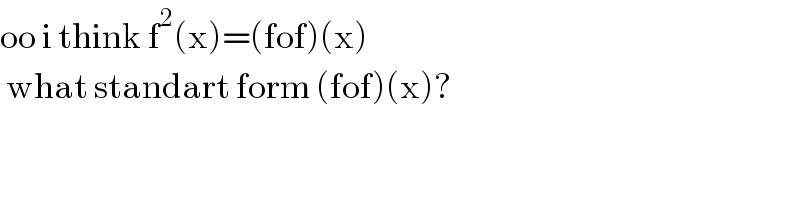
$$\mathrm{oo}\:\mathrm{i}\:\mathrm{think}\:\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)=\left(\mathrm{fof}\right)\left(\mathrm{x}\right)\: \\ $$$$\:\mathrm{what}\:\mathrm{standart}\:\mathrm{form}\:\left(\mathrm{fof}\right)\left(\mathrm{x}\right)? \\ $$
Commented by MJS_new last updated on 24/Feb/22

$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{what}'\mathrm{s}\:\mathrm{standard}\:\mathrm{nowadays}. \\ $$$$\mathrm{also}\:{f}\circ{g}\:\mathrm{for}\:\mathrm{some}\:\mathrm{means}\:{f}\left({g}\left({x}\right)\right)\:\mathrm{and}\:\mathrm{for} \\ $$$$\mathrm{others}\:{g}\left({f}\left({x}\right)\right) \\ $$$$\mathrm{too}\:\mathrm{much}\:\mathrm{confusion} \\ $$$$\mathrm{if}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{means}\:\left(\mathrm{sin}\:{x}\right)^{\mathrm{2}} \:\mathrm{then}\:\mathrm{why}\:\mathrm{sin}^{−\mathrm{1}} \:{x} \\ $$$$\mathrm{doesn}'\mathrm{t}\:\mathrm{mean}\:\left(\mathrm{sin}\:{x}\right)^{−\mathrm{1}} ? \\ $$$$\mathrm{what}\:\mathrm{about}\:\mathrm{ln}^{−\mathrm{1}} \:{x}?\:\mathrm{is}\:\mathrm{it}\:\frac{\mathrm{1}}{\mathrm{ln}\:{x}}\:\mathrm{or}\:\mathrm{e}^{{x}} ? \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{use}\:{f}^{\:{n}} \left({x}\right)\:\mathrm{for}\:\mathrm{the}\:{n}^{\mathrm{th}} \:\mathrm{derivate}\:\mathrm{then}\:\mathrm{why} \\ $$$${f}^{\:−\mathrm{1}} \left({x}\right)\:\neq\:\int{f}\left({x}\right){dx}? \\ $$$$\mathrm{better}\:\mathrm{ask}\:\mathrm{in}\:\mathrm{each}\:\mathrm{case}\:\mathrm{what}\:\mathrm{is}\:\mathrm{meant}... \\ $$
Commented by cortano1 last updated on 24/Feb/22

$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mahdipoor last updated on 23/Feb/22
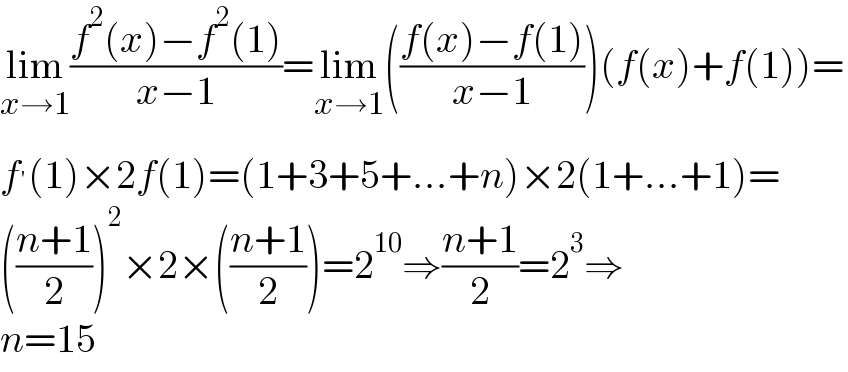
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{f}^{\mathrm{2}} \left({x}\right)−{f}^{\mathrm{2}} \left(\mathrm{1}\right)}{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{{f}\left({x}\right)−{f}\left(\mathrm{1}\right)}{{x}−\mathrm{1}}\right)\left({f}\left({x}\right)+{f}\left(\mathrm{1}\right)\right)= \\ $$$${f}^{'} \left(\mathrm{1}\right)×\mathrm{2}{f}\left(\mathrm{1}\right)=\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+...+{n}\right)×\mathrm{2}\left(\mathrm{1}+...+\mathrm{1}\right)= \\ $$$$\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{2}×\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}^{\mathrm{10}} \Rightarrow\frac{{n}+\mathrm{1}}{\mathrm{2}}=\mathrm{2}^{\mathrm{3}} \Rightarrow \\ $$$${n}=\mathrm{15} \\ $$
