
Question and Answers Forum
Question Number 166723 by cortano1 last updated on 26/Feb/22
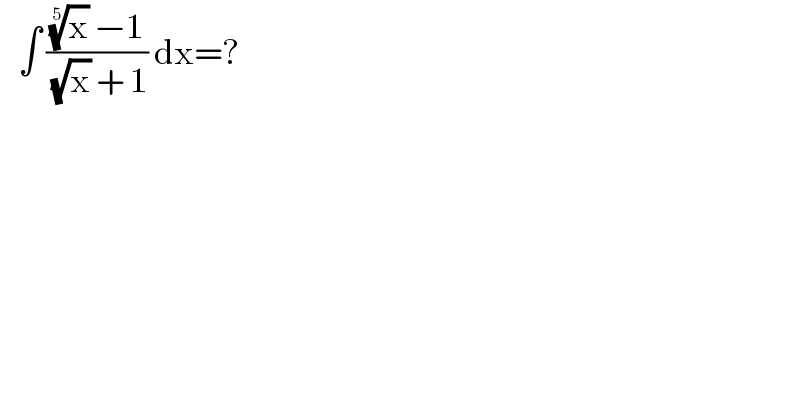
Answered by MJS_new last updated on 26/Feb/22
![∫((x^(1/5) −1)/(x^(1/2) +1))dx= [t=x^(1/10) → dx=10t^9 dt] =10∫((t^9 (t^2 −1))/(t^5 +1))dt=10∫((t^9 (t−1))/(t^4 −t^3 +t^2 −t+1))dt= =10∫((t^9 (t−1))/((t^2 −((1+(√5))/2)t+1)(t^2 −((1−(√5))/2)t+1)))dt= =I_1 +I_2 +I_3 +I_4 +I_5 with I_1 =10∫(t^6 −t^4 −t)dt=((10)/7)t^7 −2t^5 −5t^2 I_2 =∫(((5−(√5))t−(√5))/(t^2 −((1+(√5))/2)t+1))dt=((5−(√5))/2)ln (t^2 −((1+(√5))/2)t+1) I_3 =∫(((5+(√5))t+(√5))/(t^2 −((1−(√5))/2)t+1))dt=((5+(√5))/2)ln (t^2 −((1−(√5))/2)t+1) I_4 =(√5)∫(dt/(t^2 −((1+(√5))/2)t+1))=(√(2(5+(√5))))arctan (((√(10(5+(√5))))(t−((1+(√5))/4)))/5) I_5 =−(√5)∫(dt/(t^2 −((1−(√5))/2)t+1))=−(√(2(5−(√5))))arctan (((√(10(5−(√5))))(t−((1−(√5))/4)))/5) ...](Q166748.png)
| ||
Question and Answers Forum | ||
Question Number 166723 by cortano1 last updated on 26/Feb/22 | ||
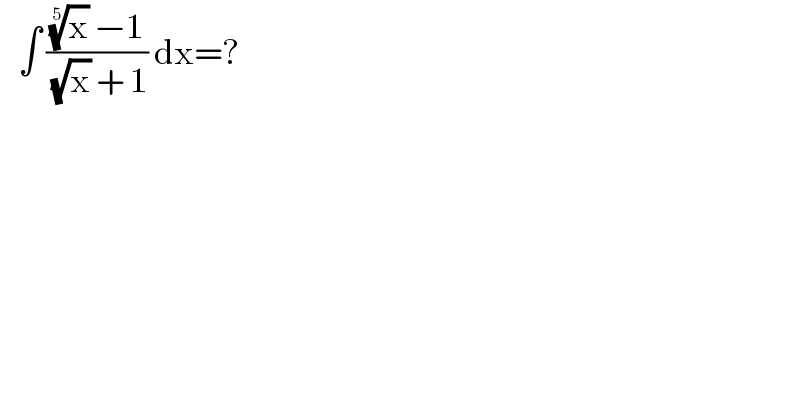 | ||
Answered by MJS_new last updated on 26/Feb/22 | ||
![∫((x^(1/5) −1)/(x^(1/2) +1))dx= [t=x^(1/10) → dx=10t^9 dt] =10∫((t^9 (t^2 −1))/(t^5 +1))dt=10∫((t^9 (t−1))/(t^4 −t^3 +t^2 −t+1))dt= =10∫((t^9 (t−1))/((t^2 −((1+(√5))/2)t+1)(t^2 −((1−(√5))/2)t+1)))dt= =I_1 +I_2 +I_3 +I_4 +I_5 with I_1 =10∫(t^6 −t^4 −t)dt=((10)/7)t^7 −2t^5 −5t^2 I_2 =∫(((5−(√5))t−(√5))/(t^2 −((1+(√5))/2)t+1))dt=((5−(√5))/2)ln (t^2 −((1+(√5))/2)t+1) I_3 =∫(((5+(√5))t+(√5))/(t^2 −((1−(√5))/2)t+1))dt=((5+(√5))/2)ln (t^2 −((1−(√5))/2)t+1) I_4 =(√5)∫(dt/(t^2 −((1+(√5))/2)t+1))=(√(2(5+(√5))))arctan (((√(10(5+(√5))))(t−((1+(√5))/4)))/5) I_5 =−(√5)∫(dt/(t^2 −((1−(√5))/2)t+1))=−(√(2(5−(√5))))arctan (((√(10(5−(√5))))(t−((1−(√5))/4)))/5) ...](Q166748.png) | ||
| ||