
Question and Answers Forum
Question Number 166756 by HongKing last updated on 27/Feb/22
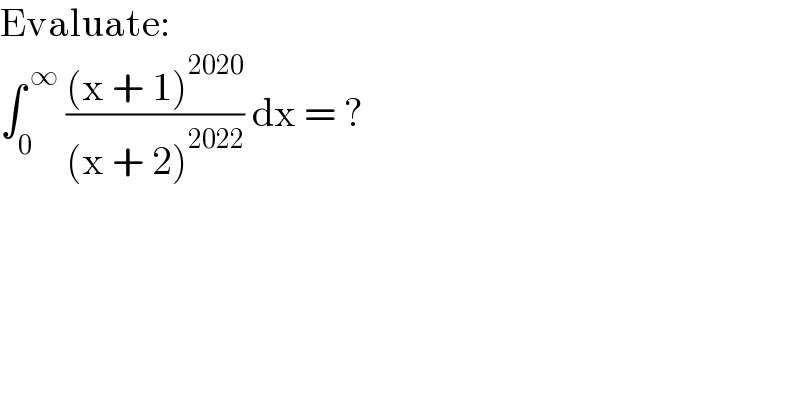
Answered by Mathspace last updated on 27/Feb/22
![x+2=t ⇒I=∫_2 ^∞ (((t−1)^(2020) )/t^(2022) )dt =∫_2 ^∞ ((Σ_(k=0) ^(2020) C_(2020) ^k t^k (−1)^(2020−k) )/t^(2022) )dt =Σ_(k=0) ^(2020) (−1)^k C_(2020) ^k t^(k−2022) dt =Σ_(k=0) ^(2020) (−1)^k C_(2020) ^k [(1/(k−2021))t^(k−2022) ]_2 ^∞ =−Σ_(k=0) ^(2020) (((−1)^k C_(2020) ^k )/(k−2021)) 2^(k−2022)](Q166772.png)
Answered by mathsmine last updated on 27/Feb/22
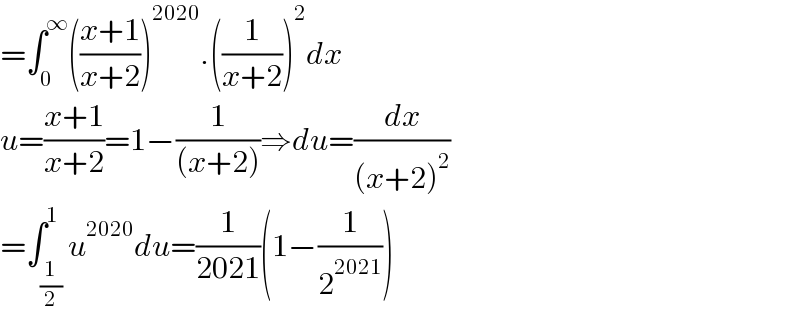
| ||
Question and Answers Forum | ||
Question Number 166756 by HongKing last updated on 27/Feb/22 | ||
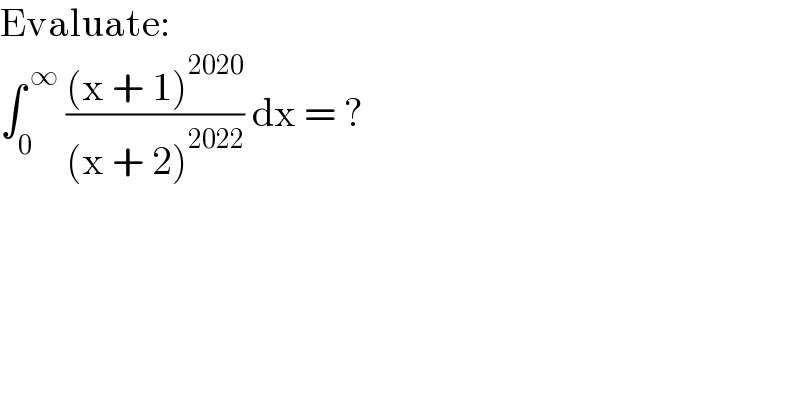 | ||
Answered by Mathspace last updated on 27/Feb/22 | ||
![x+2=t ⇒I=∫_2 ^∞ (((t−1)^(2020) )/t^(2022) )dt =∫_2 ^∞ ((Σ_(k=0) ^(2020) C_(2020) ^k t^k (−1)^(2020−k) )/t^(2022) )dt =Σ_(k=0) ^(2020) (−1)^k C_(2020) ^k t^(k−2022) dt =Σ_(k=0) ^(2020) (−1)^k C_(2020) ^k [(1/(k−2021))t^(k−2022) ]_2 ^∞ =−Σ_(k=0) ^(2020) (((−1)^k C_(2020) ^k )/(k−2021)) 2^(k−2022)](Q166772.png) | ||
| ||
Answered by mathsmine last updated on 27/Feb/22 | ||
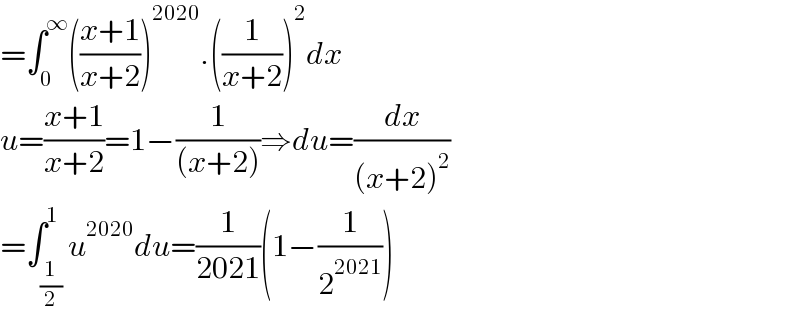 | ||
| ||