Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 166770 by mr W last updated on 27/Feb/22

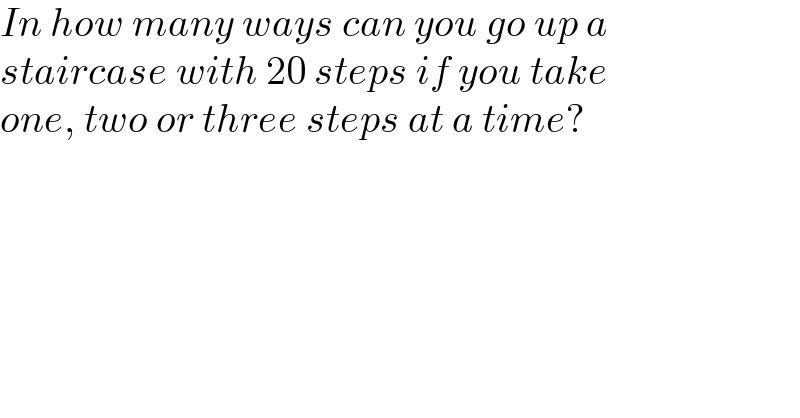
In how many ways can you go up a staircase with 20 steps if you take one, two or three steps at a time?

$${In}\:{how}\:{many}\:{ways}\:{can}\:{you}\:{go}\:{up}\:{a}\: \\ $$$${staircase}\:{with}\:\mathrm{20}\:{steps}\:{if}\:{you}\:{take}\: \\ $$$${one},\:{two}\:{or}\:{three}\:{steps}\:{at}\:{a}\:{time}? \\ $$

Commented by MJS_new last updated on 27/Feb/22

is it 121415?

$$\mathrm{is}\:\mathrm{it}\:\mathrm{121415}? \\ $$

Commented by mr W last updated on 28/Feb/22

i havn′t calculated it yet sir.

$${i}\:{havn}'{t}\:{calculated}\:{it}\:{yet}\:{sir}. \\ $$

Commented by peter frank last updated on 28/Feb/22

very tough

$$\mathrm{very}\:\mathrm{tough}\: \\ $$

Commented by MJS_new last updated on 28/Feb/22

not tough. just arrange as follows: 333333 2 333333 11 33333 221 33333 2111 33333 11111 3333 2222 3333 22211 ... then count the permutations of each row

$$\mathrm{not}\:\mathrm{tough}.\:\mathrm{just}\:\mathrm{arrange}\:\mathrm{as}\:\mathrm{follows}: \\ $$$$\mathrm{333333}\:\mathrm{2} \\ $$$$\mathrm{333333}\:\mathrm{11} \\ $$$$\mathrm{33333}\:\mathrm{221} \\ $$$$\mathrm{33333}\:\mathrm{2111} \\ $$$$\mathrm{33333}\:\mathrm{11111} \\ $$$$\mathrm{3333}\:\mathrm{2222} \\ $$$$\mathrm{3333}\:\mathrm{22211} \\ $$$$... \\ $$$$\mathrm{then}\:\mathrm{count}\:\mathrm{the}\:\mathrm{permutations}\:\mathrm{of}\:\mathrm{each}\:\mathrm{row} \\ $$

Commented by mr W last updated on 28/Feb/22

MJS sir: 121415 is correct. i got the same.

$${MJS}\:{sir}: \\ $$$$\mathrm{121415}\:{is}\:{correct}.\:{i}\:{got}\:{the}\:{same}. \\ $$

Commented by MJS_new last updated on 28/Feb/22

thank you!

$$\mathrm{thank}\:\mathrm{you}! \\ $$

Answered by nadovic last updated on 27/Feb/22

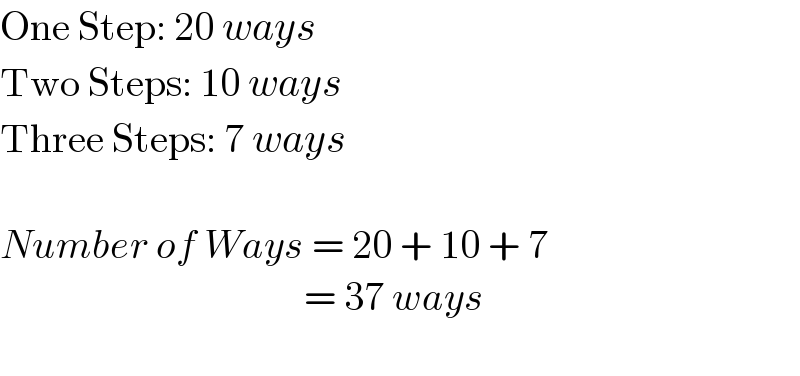
One Step: 20 ways Two Steps: 10 ways Three Steps: 7 ways Number of Ways = 20 + 10 + 7 = 37 ways

$$\mathrm{One}\:\mathrm{Step}:\:\mathrm{20}\:{ways} \\ $$$$\mathrm{Two}\:\mathrm{Steps}:\:\mathrm{10}\:{ways} \\ $$$$\mathrm{Three}\:\mathrm{Steps}:\:\mathrm{7}\:{ways} \\ $$$$ \\ $$$${Number}\:{of}\:{Ways}\:=\:\mathrm{20}\:+\:\mathrm{10}\:+\:\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{37}\:{ways} \\ $$$$ \\ $$

Commented by mr W last updated on 27/Feb/22

wrong!

$${wrong}! \\ $$

Answered by nadovic last updated on 28/Feb/22

= ^(20) P_1 +^(20) P_2 +^(20) P_3 = 7240 ways

$$\:\:\:\:\:\:=\:\:^{\mathrm{20}} \mathrm{P}_{\mathrm{1}} \:+\:^{\mathrm{20}} \mathrm{P}_{\mathrm{2}} \:+\:^{\mathrm{20}} \mathrm{P}_{\mathrm{3}} \\ $$$$\:\:\:\:\:=\:\mathrm{7240}\:{ways} \\ $$

Commented by MJS_new last updated on 28/Feb/22

maybe test your hypothetical formula with an easy example? 5 stairs: 32 23 311 131 113 221 212 122 2111 1211 1121 1112 11111 13 possibilities 6 stairs: 33 321 312 231 213 132 123 3111 1311 1131 1113 222 2211 2121 2112 1221 1212 1122 21111 12111 11211 11121 11112 111111 24 possibilities ...

$$\mathrm{maybe}\:\mathrm{test}\:\mathrm{your}\:\mathrm{hypothetical}\:\mathrm{formula}\:\mathrm{with} \\ $$$$\mathrm{an}\:\mathrm{easy}\:\mathrm{example}? \\ $$$$\mathrm{5}\:\mathrm{stairs}: \\ $$$$\mathrm{32}\:\mathrm{23}\:\mathrm{311}\:\mathrm{131}\:\mathrm{113}\:\mathrm{221}\:\mathrm{212}\:\mathrm{122}\:\mathrm{2111}\:\mathrm{1211} \\ $$$$\mathrm{1121}\:\mathrm{1112}\:\mathrm{11111} \\ $$$$\mathrm{13}\:\mathrm{possibilities} \\ $$$$\mathrm{6}\:\mathrm{stairs}: \\ $$$$\mathrm{33}\:\mathrm{321}\:\mathrm{312}\:\mathrm{231}\:\mathrm{213}\:\mathrm{132}\:\mathrm{123}\:\mathrm{3111}\:\mathrm{1311}\:\mathrm{1131} \\ $$$$\mathrm{1113}\:\mathrm{222}\:\mathrm{2211}\:\mathrm{2121}\:\mathrm{2112}\:\mathrm{1221}\:\mathrm{1212}\:\mathrm{1122} \\ $$$$\mathrm{21111}\:\mathrm{12111}\:\mathrm{11211}\:\mathrm{11121}\:\mathrm{11112}\:\mathrm{111111} \\ $$$$\mathrm{24}\:\mathrm{possibilities} \\ $$$$... \\ $$

Answered by mr W last updated on 01/Mar/22

let′s look at the case that we make n moves to go up the staircase. each move can be of one, two or three steps. the number of ways to go up the staircase in n moves is the number of integer solutions of the equation a_1 +a_2 +a_3 +...+a_n =20 with 1≤a_i ≤3. using generating function it is the coefficient of the x^(20) term in the expansion of (x+x^2 +x^3 )^n . (x+x^2 +x^3 )^n =x^n (1+x+x^2 )^n =((x^n (1−x^3 )^n )/((1−x)^n )) =x^n {Σ_(k=0) ^n (−1)^k C_k ^n x^(3k) }{Σ_(m=0) ^∞ C_(n−1) ^(m+n−1) x^m } x^n x^(3k) x^m =x^(n+3k+m) =^! x^(20) n+3k+m=^! 20 ⇒3k+m=20−n 0≤k≤n, m≥0 ⇒7≤n≤20 (this is clear, we need at least 7 moves and at most 20 moves to go up the staircase.) example n=10: k=0, m=10 ⇒C_0 ^(10) C_9 ^(19) =92378 k=1, m=7 ⇒−C_1 ^(10) C_9 ^(16) =−114400 k=2, m=4 ⇒C_2 ^(10) C_9 ^(13) =32175 k=3, m=1 ⇒−C_3 ^(10) C_9 ^(10) =−1200 that means the coef. of x^(20) is 92378−114400+32175−1200=8953 the results for all values of n see following table. the total result is 121415. i.e. there are 121415 ways to go up the staircase.

$${let}'{s}\:{look}\:{at}\:{the}\:{case}\:{that}\:{we}\:{make}\:{n}\: \\ $$$${moves}\:{to}\:{go}\:{up}\:{the}\:{staircase}.\:{each}\: \\ $$$${move}\:{can}\:{be}\:{of}\:{one},\:{two}\:{or}\:{three}\: \\ $$$${steps}. \\ $$$$ \\ $$$${the}\:{number}\:{of}\:{ways}\:{to}\:{go}\:{up}\:{the} \\ $$$${staircase}\:{in}\:{n}\:{moves}\:{is}\:{the}\:{number} \\ $$$${of}\:{integer}\:{solutions}\:{of}\:{the}\:{equation} \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +...+{a}_{{n}} =\mathrm{20} \\ $$$${with}\:\mathrm{1}\leqslant{a}_{{i}} \leqslant\mathrm{3}. \\ $$$${using}\:{generating}\:{function}\:{it}\:{is}\:{the}\: \\ $$$${coefficient}\:{of}\:{the}\:{x}^{\mathrm{20}} \:{term}\:{in}\:{the} \\ $$$${expansion}\:{of}\:\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)^{{n}} . \\ $$$$ \\ $$$$\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)^{{n}} \\ $$$$={x}^{{n}} \left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{{n}} \\ $$$$=\frac{{x}^{{n}} \left(\mathrm{1}−{x}^{\mathrm{3}} \right)^{{n}} }{\left(\mathrm{1}−{x}\right)^{{n}} } \\ $$$$={x}^{{n}} \left\{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{{n}} {x}^{\mathrm{3}{k}} \right\}\left\{\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{n}−\mathrm{1}} ^{{m}+{n}−\mathrm{1}} {x}^{{m}} \right\} \\ $$$${x}^{{n}} {x}^{\mathrm{3}{k}} {x}^{{m}} ={x}^{{n}+\mathrm{3}{k}+{m}} \overset{!} {=}{x}^{\mathrm{20}} \\ $$$${n}+\mathrm{3}{k}+{m}\overset{!} {=}\mathrm{20} \\ $$$$\Rightarrow\mathrm{3}{k}+{m}=\mathrm{20}−{n} \\ $$$$\mathrm{0}\leqslant{k}\leqslant{n},\:{m}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{7}\leqslant{n}\leqslant\mathrm{20}\:\left({this}\:{is}\:{clear},\:{we}\:{need}\:{at}\right. \\ $$$${least}\:\mathrm{7}\:{moves}\:{and}\:{at}\:{most}\:\mathrm{20}\:{moves} \\ $$$$\left.{to}\:{go}\:{up}\:{the}\:{staircase}.\right) \\ $$$$ \\ $$$${example}\:{n}=\mathrm{10}: \\ $$$${k}=\mathrm{0},\:{m}=\mathrm{10}\:\Rightarrow{C}_{\mathrm{0}} ^{\mathrm{10}} {C}_{\mathrm{9}} ^{\mathrm{19}} =\mathrm{92378} \\ $$$${k}=\mathrm{1},\:{m}=\mathrm{7}\:\Rightarrow−{C}_{\mathrm{1}} ^{\mathrm{10}} {C}_{\mathrm{9}} ^{\mathrm{16}} =−\mathrm{114400} \\ $$$${k}=\mathrm{2},\:{m}=\mathrm{4}\:\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{10}} {C}_{\mathrm{9}} ^{\mathrm{13}} =\mathrm{32175} \\ $$$${k}=\mathrm{3},\:{m}=\mathrm{1}\:\Rightarrow−{C}_{\mathrm{3}} ^{\mathrm{10}} {C}_{\mathrm{9}} ^{\mathrm{10}} =−\mathrm{1200} \\ $$$${that}\:{means}\:{the}\:{coef}.\:{of}\:{x}^{\mathrm{20}} \:{is} \\ $$$$\mathrm{92378}−\mathrm{114400}+\mathrm{32175}−\mathrm{1200}=\mathrm{8953} \\ $$$$ \\ $$$${the}\:{results}\:{for}\:{all}\:{values}\:{of}\:{n}\:{see} \\ $$$${following}\:{table}. \\ $$$$ \\ $$$${the}\:{total}\:{result}\:{is}\:\mathrm{121415}.\:{i}.{e}.\:{there} \\ $$$${are}\:\mathrm{121415}\:{ways}\:{to}\:{go}\:{up}\:{the}\:{staircase}. \\ $$

Commented by mr W last updated on 28/Feb/22

Commented by Tawa11 last updated on 28/Feb/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 02/Mar/22

AN OTHER METHOD let′s say there are N(n) ways to go up a staircase with n steps. if we make a move with one step, then there are n−1 steps remaining and there are N(n−1) ways to go up the remaining steps. if we make a move with two steps, then there are n−2 steps remaining and there are N(n−2) ways to go up the remaining steps. similarly if we make a move with three steps, then there are N(n−3) ways to go up the remaining steps. therefore we have following recurrence relation: N(n)=N(n−1)+N(n−2)+N(n−3) we also have N(1)=1 N(2)=2 N(3)=4 applying the recurrence relation above, we get N(4)=7 N(5)=13 N(6)=24 N(7)=44 N(8)=81 N(9)=149 N(10)=274 N(11)=504 N(12)=927 N(13)=1705 N(14)=3136 N(15)=5768 N(16)=10609 N(17)=19513 N(18)=35890 N(19)=66012 N(20)=121415 ✓ we can also find a closed formula for N(n) by solving following characteristic equation λ^3 −λ^2 −λ−1=0 let λ=s+(1/3) s^2 −(4/3)s−((38)/(27))=0 with u=((3(√(33))+19))^(1/3) , v=((3(√(33))−19))^(1/3) λ_1 =(1/3)(1+u−v) λ_(2,3) =(1/6)[2−u+v±(√3)(u+v)i] ⇒N(n)=Aλ_1 ^n +Bλ_2 ^n +Cλ_3 ^n N(0)=N(3)−N(2)−N(1)=1 N(−1)=N(2)−N(1)−N(0)=0 N(1)=Aλ_1 +Bλ_2 +Cλ_3 =1 N(0)=A+B+C=1 N(−1)=(A/λ_1 )+(B/λ_2 )+(C/λ_3 )=0 [(λ_1 ,λ_2 ,λ_3 ),(1,1,1),((1/λ_1 ),(1/λ_2 ),(1/λ_3 )) ] ((A),(B),(C) ) = ((1),(1),(0) ) ⇒ ((A),(B),(C) ) = [(λ_1 ,λ_2 ,λ_3 ),(1,1,1),((1/λ_1 ),(1/λ_2 ),(1/λ_3 )) ]^(−1) ((1),(1),(0) )

$$\boldsymbol{{AN}}\:\boldsymbol{{OTHER}}\:\boldsymbol{{METHOD}} \\ $$$${let}'{s}\:{say}\:{there}\:{are}\:{N}\left({n}\right)\:{ways}\:{to}\:{go}\:{up} \\ $$$${a}\:{staircase}\:{with}\:{n}\:{steps}.\:{if}\:{we}\:{make} \\ $$$${a}\:{move}\:{with}\:{one}\:{step},\:{then}\:{there}\:{are} \\ $$$${n}−\mathrm{1}\:{steps}\:{remaining}\:{and}\:{there}\:{are} \\ $$$${N}\left({n}−\mathrm{1}\right)\:{ways}\:{to}\:{go}\:{up}\:{the}\:{remaining} \\ $$$${steps}.\:{if}\:{we}\:{make}\:{a}\:{move}\:{with} \\ $$$${two}\:{steps},\:{then}\:{there}\:{are}\:{n}−\mathrm{2}\:{steps}\: \\ $$$${remaining}\:{and}\:{there}\:{are}\:{N}\left({n}−\mathrm{2}\right)\: \\ $$$${ways}\:{to}\:{go}\:{up}\:{the}\:{remaining}\:{steps}.\: \\ $$$${similarly}\:{if}\:{we}\:{make}\:{a}\:{move}\:{with}\: \\ $$$${three}\:{steps},\:{then}\:{there}\:{are}\:{N}\left({n}−\mathrm{3}\right)\: \\ $$$${ways}\:{to}\:{go}\:{up}\:{the}\:{remaining}\:{steps}.\: \\ $$$${therefore}\:{we}\:{have}\:{following} \\ $$$${recurrence}\:{relation}: \\ $$$${N}\left({n}\right)={N}\left({n}−\mathrm{1}\right)+{N}\left({n}−\mathrm{2}\right)+{N}\left({n}−\mathrm{3}\right) \\ $$$${we}\:{also}\:{have}\: \\ $$$${N}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${N}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$${N}\left(\mathrm{3}\right)=\mathrm{4} \\ $$$${applying}\:{the}\:{recurrence}\:{relation}\:{above},\: \\ $$$${we}\:{get} \\ $$$${N}\left(\mathrm{4}\right)=\mathrm{7} \\ $$$${N}\left(\mathrm{5}\right)=\mathrm{13} \\ $$$${N}\left(\mathrm{6}\right)=\mathrm{24} \\ $$$${N}\left(\mathrm{7}\right)=\mathrm{44} \\ $$$${N}\left(\mathrm{8}\right)=\mathrm{81} \\ $$$${N}\left(\mathrm{9}\right)=\mathrm{149} \\ $$$${N}\left(\mathrm{10}\right)=\mathrm{274} \\ $$$${N}\left(\mathrm{11}\right)=\mathrm{504} \\ $$$${N}\left(\mathrm{12}\right)=\mathrm{927} \\ $$$${N}\left(\mathrm{13}\right)=\mathrm{1705} \\ $$$${N}\left(\mathrm{14}\right)=\mathrm{3136} \\ $$$${N}\left(\mathrm{15}\right)=\mathrm{5768} \\ $$$${N}\left(\mathrm{16}\right)=\mathrm{10609} \\ $$$${N}\left(\mathrm{17}\right)=\mathrm{19513} \\ $$$${N}\left(\mathrm{18}\right)=\mathrm{35890} \\ $$$${N}\left(\mathrm{19}\right)=\mathrm{66012} \\ $$$${N}\left(\mathrm{20}\right)=\mathrm{121415}\:\checkmark \\ $$$$ \\ $$$${we}\:{can}\:{also}\:{find}\:{a}\:{closed}\:{formula} \\ $$$${for}\:{N}\left({n}\right)\:{by}\:{solving}\:{following} \\ $$$${characteristic}\:{equation} \\ $$$$\lambda^{\mathrm{3}} −\lambda^{\mathrm{2}} −\lambda−\mathrm{1}=\mathrm{0} \\ $$$${let}\:\lambda={s}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${s}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{s}−\frac{\mathrm{38}}{\mathrm{27}}=\mathrm{0} \\ $$$${with}\:{u}=\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt{\mathrm{33}}+\mathrm{19}},\:{v}=\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt{\mathrm{33}}−\mathrm{19}} \\ $$$$\lambda_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+{u}−{v}\right) \\ $$$$\lambda_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{2}−{u}+{v}\pm\sqrt{\mathrm{3}}\left({u}+{v}\right){i}\right] \\ $$$$\Rightarrow{N}\left({n}\right)={A}\lambda_{\mathrm{1}} ^{{n}} +{B}\lambda_{\mathrm{2}} ^{{n}} +{C}\lambda_{\mathrm{3}} ^{{n}} \\ $$$${N}\left(\mathrm{0}\right)={N}\left(\mathrm{3}\right)−{N}\left(\mathrm{2}\right)−{N}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${N}\left(−\mathrm{1}\right)={N}\left(\mathrm{2}\right)−{N}\left(\mathrm{1}\right)−{N}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$ \\ $$$${N}\left(\mathrm{1}\right)={A}\lambda_{\mathrm{1}} +{B}\lambda_{\mathrm{2}} +{C}\lambda_{\mathrm{3}} =\mathrm{1} \\ $$$${N}\left(\mathrm{0}\right)={A}+{B}+{C}=\mathrm{1} \\ $$$${N}\left(−\mathrm{1}\right)=\frac{{A}}{\lambda_{\mathrm{1}} }+\frac{{B}}{\lambda_{\mathrm{2}} }+\frac{{C}}{\lambda_{\mathrm{3}} }=\mathrm{0} \\ $$$$\begin{bmatrix}{\lambda_{\mathrm{1}} }&{\lambda_{\mathrm{2}} }&{\lambda_{\mathrm{3}} }\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\frac{\mathrm{1}}{\lambda_{\mathrm{1}} }}&{\frac{\mathrm{1}}{\lambda_{\mathrm{2}} }}&{\frac{\mathrm{1}}{\lambda_{\mathrm{3}} }}\end{bmatrix}\begin{pmatrix}{{A}}\\{{B}}\\{{C}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\Rightarrow\begin{pmatrix}{{A}}\\{{B}}\\{{C}}\end{pmatrix}\:=\begin{bmatrix}{\lambda_{\mathrm{1}} }&{\lambda_{\mathrm{2}} }&{\lambda_{\mathrm{3}} }\\{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\frac{\mathrm{1}}{\lambda_{\mathrm{1}} }}&{\frac{\mathrm{1}}{\lambda_{\mathrm{2}} }}&{\frac{\mathrm{1}}{\lambda_{\mathrm{3}} }}\end{bmatrix}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\\{\mathrm{0}}\end{pmatrix} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com