
Question and Answers Forum
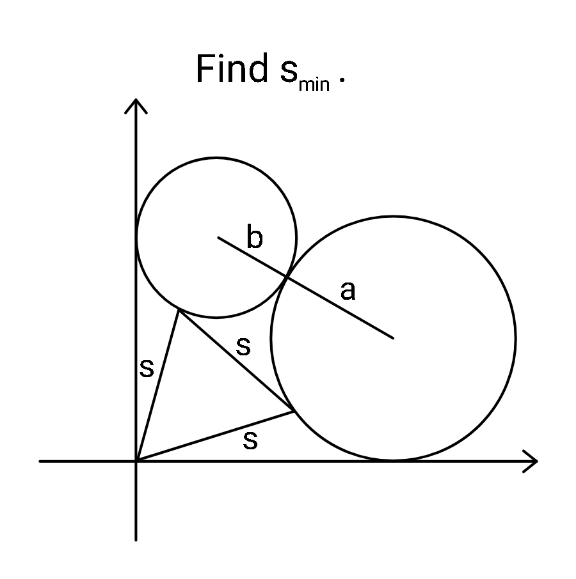
Question Number 166779 by ajfour last updated on 27/Feb/22
Answered by mr W last updated on 27/Feb/22
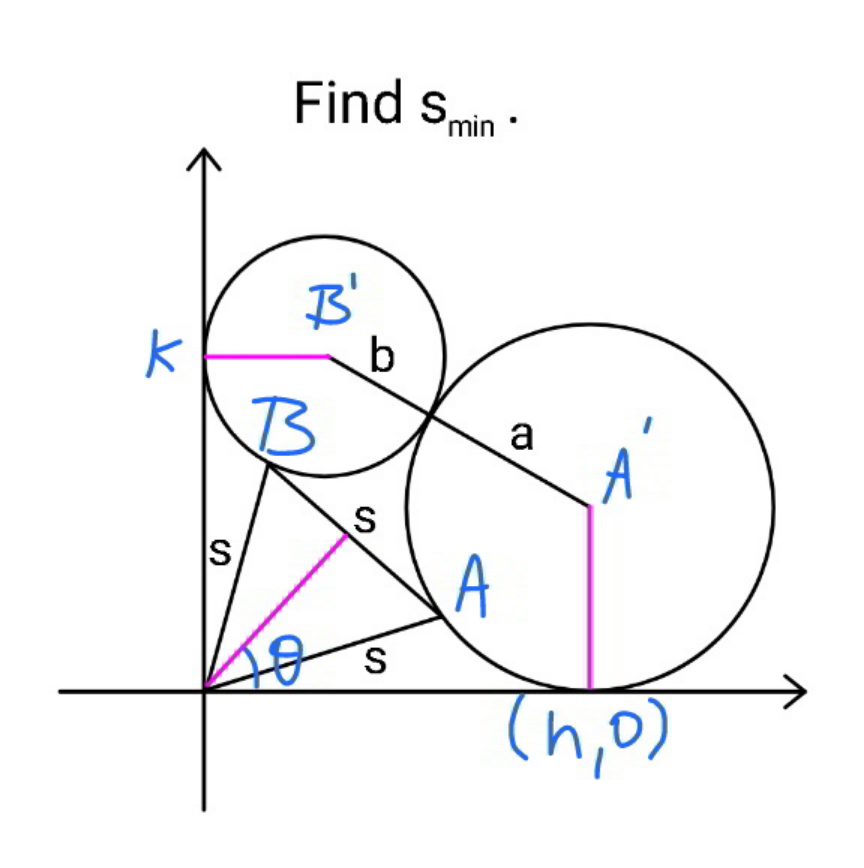
Commented by mr W last updated on 28/Feb/22
![A′(h,a) B′(b,k) (h−b)^2 +(k−a)^2 =(a+b)^2 k^2 −2ak+h^2 −2b(h+a)=0 ⇒k=a+(√((a+2b−h)(h+a))) x_A =(s/2)((√3)cos θ+sin θ) y_A =(s/2)((√3)sin θ−cos θ) x_B =(s/2)((√3)cos θ−sin θ) y_B =(s/2)((√3)sin θ+cos θ) ((s/2)((√3)cos θ+sin θ)−h)^2 +((s/2)((√3)sin θ−cos θ)−a)^2 =a^2 s^2 −[((√3)h−a)cos θ+((√3)a+h)sin θ]s+h^2 =0 ...(i) ((s/2)((√3)cos θ−sin θ)−b)^2 +((s/2)((√3)sin θ+cos θ)−k)^2 =b^2 s^2 −[((√3)b+k)cos θ+((√3)k−b)sin θ]s+k^2 =0 ...(ii) ((√3)h−a)cos θ+((√3)a+h)sin θ=((s^2 +h^2 )/s) cos (θ−tan^(−1) (((√3)a+h)/( (√3)h−a)))=((s^2 +h^2 )/( 2s(√(h^2 +a^2 )))) ⇒θ=tan^(−1) (((√3)a+h)/( (√3)h−a))+cos^(−1) ((s^2 +h^2 )/( 2s(√(h^2 +a^2 )))) s^2 −2s(√(k^2 +b^2 )) cos (θ−tan^(−1) (((√3)k−b)/( (√3)b+k)))+k^2 =0 s^2 −2s(√(k^2 +b^2 )) cos (cos^(−1) ((s^2 −h^2 )/( 2s(√(h^2 +a^2 ))))+tan^(−1) (((√3)a+h)/( (√3)h−a))−tan^(−1) (((√3)k−b)/( (√3)b+k)))+k^2 =0 ...](Q166781.png)
Commented by ajfour last updated on 28/Feb/22
![(h−scos α)^2 +(a−ssin α)^2 =a^2 (b−ssin β)^2 +(k−scos β)^2 =b^2 ⇒ h=scos α+(√(a^2 −(a−ssin α)^2 )) k=scos β+(√(b^2 −(b−ssin β)^2 )) α+β=(π/6) ; α−β=2θ ⇒ α=(π/(12))+θ , β=(π/(12))−θ (h−b)^2 +(k−a)^2 =(a+b)^2 ⇒ {scos ((π/(12))+θ) −b+(√(a^2 −[a−ssin ((π/(12))+θ)]^2 ))}^2 +{scos ((π/(12))−θ)−a+(√(b^2 −[b−ssin ((π/(12))−θ)]^2 ))}^2 =(a+b)^2](Q166794.png)
Commented by mr W last updated on 28/Feb/22

Commented by Tawa11 last updated on 28/Feb/22

