
Question and Answers Forum
Question Number 166956 by mnjuly1970 last updated on 03/Mar/22
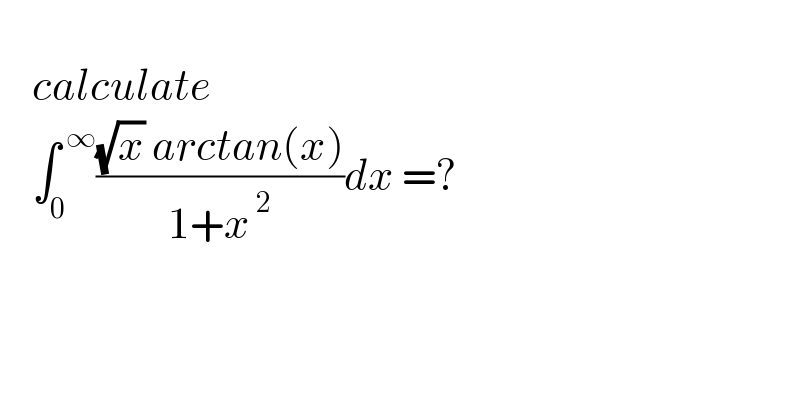
Answered by ArielVyny last updated on 03/Mar/22
![dt=((arctan(x))/(1+x^2 ))dx→t=(1/2)(arctanx)^2 (√(2t))=arctanx→x=arctan((√2)t) ∫_0 ^(π^2 /( 8)) arctan((√2)t)dt= (1/( (√2)))∫_0 ^(π^2 /8) arctan(u)du we cant stop here =Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+1))∫_0 ^(π^2 /8) t^(2n+1) dt =Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+1))[(1/(2n+2))(π^2 /8)] =(π^2 /8)Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/((2n+1)(2n+2))) =(π^2 /8)[Σ(((−1)^n ((√2))^(2n+1) )/(2n+1))]−(π^2 /8)Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+2)) =(π^2 /8)arctan((√2))(π^2 /(16))Σ_(n≥1) (((−1)^(n+1) (2)^n )/n) =(π^2 /8)arctan((√2))+(π^2 /(16))ln(3)](Q166969.png)
| ||
Question and Answers Forum | ||
Question Number 166956 by mnjuly1970 last updated on 03/Mar/22 | ||
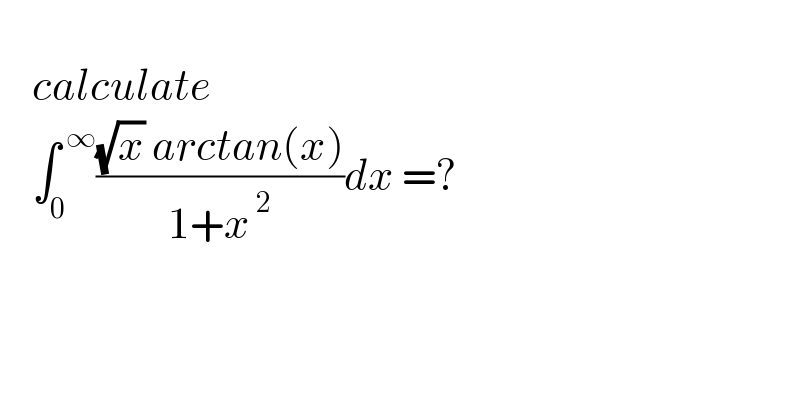 | ||
Answered by ArielVyny last updated on 03/Mar/22 | ||
![dt=((arctan(x))/(1+x^2 ))dx→t=(1/2)(arctanx)^2 (√(2t))=arctanx→x=arctan((√2)t) ∫_0 ^(π^2 /( 8)) arctan((√2)t)dt= (1/( (√2)))∫_0 ^(π^2 /8) arctan(u)du we cant stop here =Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+1))∫_0 ^(π^2 /8) t^(2n+1) dt =Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+1))[(1/(2n+2))(π^2 /8)] =(π^2 /8)Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/((2n+1)(2n+2))) =(π^2 /8)[Σ(((−1)^n ((√2))^(2n+1) )/(2n+1))]−(π^2 /8)Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+2)) =(π^2 /8)arctan((√2))(π^2 /(16))Σ_(n≥1) (((−1)^(n+1) (2)^n )/n) =(π^2 /8)arctan((√2))+(π^2 /(16))ln(3)](Q166969.png) | ||
| ||