
Question Number 167040 by cortano1 last updated on 05/Mar/22
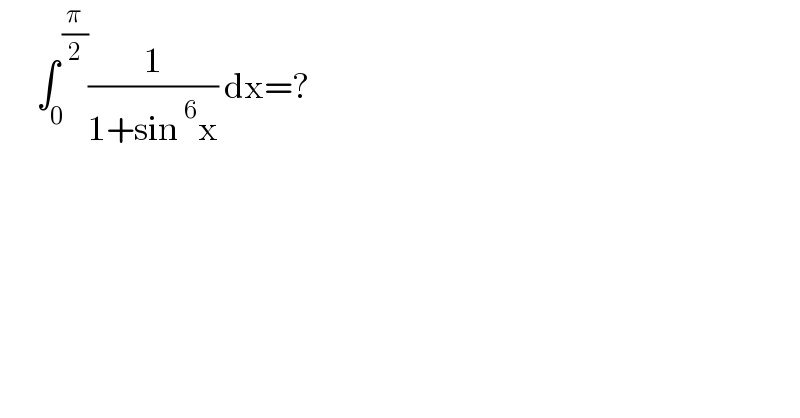
$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:^{\mathrm{6}} \mathrm{x}}\:\mathrm{dx}=? \\ $$
Commented by greogoury55 last updated on 05/Mar/22
![I=∫_0 ^(π/2) ((sec^6 x)/(sec^6 x+tan^6 x)) dx =^(t=tan x) ∫_0 ^∞ (((1+t^2 )^2 )/((1+t^2 )^3 +t^6 )) dt = ∫_0 ^∞ ((t^4 +2t^2 +1)/((2t^2 +1)(t^4 +t^2 +1))) dt = (1/3)[∫_0 ^∞ (dt/(2t^2 +1)) +∫_0 ^∞ ((t^2 +2)/(t^4 +t^2 +1)) dt ] = (π/(12))((√2)+2(√3) )](Q167046.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}\:^{\mathrm{6}} {x}}{\mathrm{sec}\:^{\mathrm{6}} {x}+\mathrm{tan}\:^{\mathrm{6}} {x}}\:{dx}\: \\ $$$$\:\overset{{t}=\mathrm{tan}\:{x}} {=}\:\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} +{t}^{\mathrm{6}} }\:{dt} \\ $$$$\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right)}\:{dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}\:+\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} +\mathrm{2}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}\:{dt}\:\right] \\ $$$$=\:\frac{\pi}{\mathrm{12}}\left(\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}\:\right) \\ $$
