Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 167185 by pete last updated on 09/Mar/22

Find the equation of the locus of a moving point P, such that its distance from the point A(4,3) and B(5,1) is in the ratio 3 : 1

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{a}\:\mathrm{moving}\:\mathrm{point}\:\mathrm{P}, \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{its}\:\mathrm{distance}\:\mathrm{from}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{A}\left(\mathrm{4},\mathrm{3}\right)\:\mathrm{and}\:\mathrm{B}\left(\mathrm{5},\mathrm{1}\right)\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{3}\::\:\mathrm{1} \\ $$

Commented by mr W last updated on 09/Mar/22

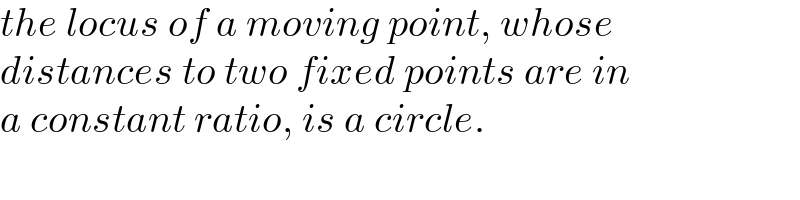
the locus of a moving point, whose distances to two fixed points are in a constant ratio, is a circle.

$${the}\:{locus}\:{of}\:{a}\:{moving}\:{point},\:{whose} \\ $$$${distances}\:{to}\:{two}\:{fixed}\:{points}\:{are}\:{in} \\ $$$${a}\:{constant}\:{ratio},\:{is}\:{a}\:{circle}. \\ $$

Commented by otchereabdullai@gmail.com last updated on 21/Mar/22

Nice!

$$\mathrm{Nice}! \\ $$

Answered by Rasheed.Sindhi last updated on 09/Mar/22

P=(x,y) ∣AP∣:∣BP∣=3:1 ∣AP∣=3∣BP∣ (√((4−x)^2 +(3−y)^2 ))=3(√((5−x)^2 +(1−y)^2 )) x^2 −8x+16+y^2 −6y+9=9(x^2 −10x+25+y^2 −2y+1) 8x^2 +8y^2 −82x−12y+209=0

$$\mathrm{P}=\left({x},{y}\right) \\ $$$$\mid\mathrm{AP}\mid:\mid\mathrm{BP}\mid=\mathrm{3}:\mathrm{1} \\ $$$$\mid\mathrm{AP}\mid=\mathrm{3}\mid\mathrm{BP}\mid \\ $$$$\sqrt{\left(\mathrm{4}−{x}\right)^{\mathrm{2}} +\left(\mathrm{3}−{y}\right)^{\mathrm{2}} }=\mathrm{3}\sqrt{\left(\mathrm{5}−{x}\right)^{\mathrm{2}} +\left(\mathrm{1}−{y}\right)^{\mathrm{2}} }\: \\ $$$${x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{16}+{y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{9}=\mathrm{9}\left({x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{25}+{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{1}\right) \\ $$$$\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}{y}^{\mathrm{2}} −\mathrm{82}{x}−\mathrm{12}{y}+\mathrm{209}=\mathrm{0} \\ $$

Answered by som(math1967) last updated on 09/Mar/22

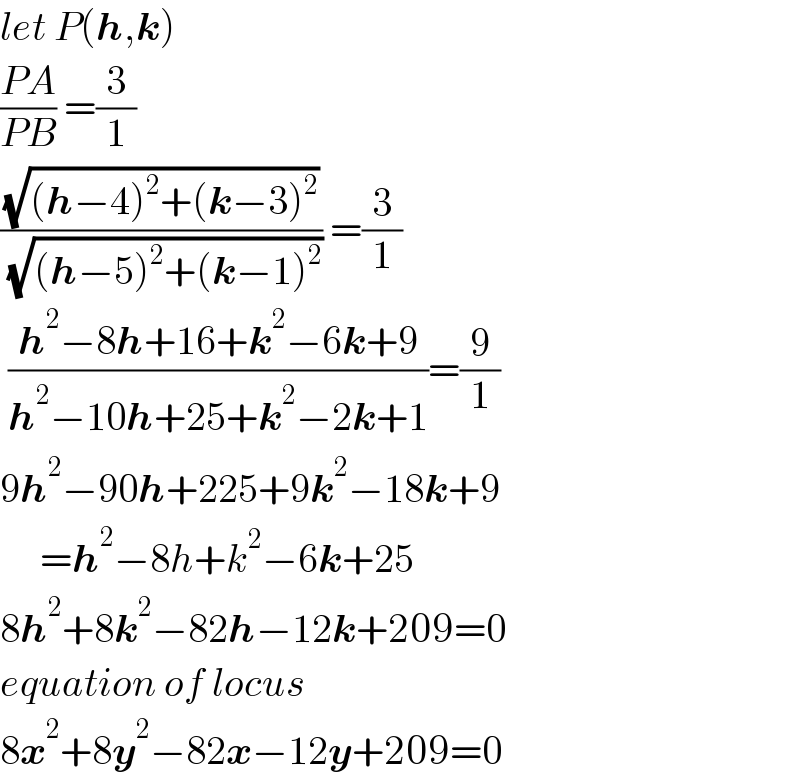
let P(h,k) ((PA)/(PB)) =(3/1) ((√((h−4)^2 +(k−3)^2 ))/( (√((h−5)^2 +(k−1)^2 )))) =(3/1) ((h^2 −8h+16+k^2 −6k+9)/(h^2 −10h+25+k^2 −2k+1))=(9/1) 9h^2 −90h+225+9k^2 −18k+9 =h^2 −8h+k^2 −6k+25 8h^2 +8k^2 −82h−12k+209=0 equation of locus 8x^2 +8y^2 −82x−12y+209=0

$${let}\:{P}\left(\boldsymbol{{h}},\boldsymbol{{k}}\right) \\ $$$$\frac{{PA}}{{PB}}\:=\frac{\mathrm{3}}{\mathrm{1}} \\ $$$$\frac{\sqrt{\left(\boldsymbol{{h}}−\mathrm{4}\right)^{\mathrm{2}} +\left(\boldsymbol{{k}}−\mathrm{3}\right)^{\mathrm{2}} }}{\:\sqrt{\left(\boldsymbol{{h}}−\mathrm{5}\right)^{\mathrm{2}} +\left(\boldsymbol{{k}}−\mathrm{1}\right)^{\mathrm{2}} }}\:=\frac{\mathrm{3}}{\mathrm{1}} \\ $$$$\:\frac{\boldsymbol{{h}}^{\mathrm{2}} −\mathrm{8}\boldsymbol{{h}}+\mathrm{16}+\boldsymbol{{k}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{k}}+\mathrm{9}}{\boldsymbol{{h}}^{\mathrm{2}} −\mathrm{10}\boldsymbol{{h}}+\mathrm{25}+\boldsymbol{{k}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{k}}+\mathrm{1}}=\frac{\mathrm{9}}{\mathrm{1}} \\ $$$$\mathrm{9}\boldsymbol{{h}}^{\mathrm{2}} −\mathrm{90}\boldsymbol{{h}}+\mathrm{225}+\mathrm{9}\boldsymbol{{k}}^{\mathrm{2}} −\mathrm{18}\boldsymbol{{k}}+\mathrm{9} \\ $$$$\:\:\:\:\:=\boldsymbol{{h}}^{\mathrm{2}} −\mathrm{8}{h}+{k}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{k}}+\mathrm{25} \\ $$$$\mathrm{8}\boldsymbol{{h}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{k}}^{\mathrm{2}} −\mathrm{82}\boldsymbol{{h}}−\mathrm{12}\boldsymbol{{k}}+\mathrm{209}=\mathrm{0} \\ $$$${equation}\:{of}\:{locus} \\ $$$$\mathrm{8}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{82}\boldsymbol{{x}}−\mathrm{12}\boldsymbol{{y}}+\mathrm{209}=\mathrm{0} \\ $$

Commented by pete last updated on 09/Mar/22

Thank you very much sir. But sir, why is the locus of the point not a straight line but a circle? That is my problem.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}.\:\mathrm{But}\:\mathrm{sir},\:\mathrm{why}\:\mathrm{is}\:\mathrm{the}\:\mathrm{locus} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:\mathrm{not}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{but}\:\mathrm{a}\:\mathrm{circle}? \\ $$$$\mathrm{That}\:\mathrm{is}\:\mathrm{my}\:\mathrm{problem}. \\ $$

Commented by som(math1967) last updated on 09/Mar/22

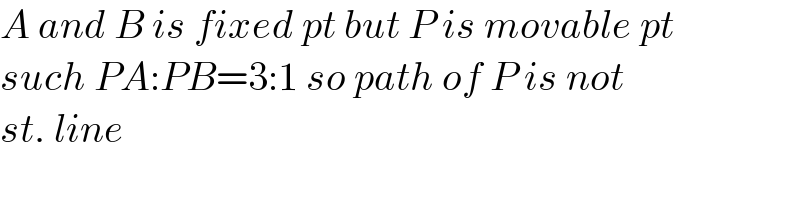
A and B is fixed pt but P is movable pt such PA:PB=3:1 so path of P is not st. line

$${A}\:{and}\:{B}\:{is}\:{fixed}\:{pt}\:{but}\:{P}\:{is}\:{movable}\:{pt} \\ $$$${such}\:{PA}:{PB}=\mathrm{3}:\mathrm{1}\:{so}\:{path}\:{of}\:{P}\:{is}\:{not} \\ $$$${st}.\:{line}\: \\ $$

Commented by MJS_new last updated on 09/Mar/22

on a straight line (= the x−axis) to given points A & B, find P with ∣AP∣:∣BP∣=3:1 this is the same problem as this: split AB with ratio 3:1 which has exactly 2 solutions (internal and external split point) P_i , P_e these are on the line itself but if you allow “split points” in 2 dimensions, how could they all form a straight line?

$$\mathrm{on}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\left(=\:\mathrm{the}\:{x}−\mathrm{axis}\right)\:\mathrm{to}\:\mathrm{given} \\ $$$$\mathrm{points}\:{A}\:\&\:{B},\:\mathrm{find}\:{P}\:\mathrm{with} \\ $$$$\mid{AP}\mid:\mid{BP}\mid=\mathrm{3}:\mathrm{1} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{problem}\:\mathrm{as}\:\mathrm{this}: \\ $$$$\mathrm{split}\:{AB}\:\mathrm{with}\:\mathrm{ratio}\:\mathrm{3}:\mathrm{1} \\ $$$$\mathrm{which}\:\mathrm{has}\:\mathrm{exactly}\:\mathrm{2}\:\mathrm{solutions}\:\left(\mathrm{internal}\:\mathrm{and}\right. \\ $$$$\left.\mathrm{external}\:\mathrm{split}\:\mathrm{point}\right)\:{P}_{{i}} ,\:{P}_{{e}} \\ $$$$\mathrm{these}\:\mathrm{are}\:\mathrm{on}\:\mathrm{the}\:\mathrm{line}\:\mathrm{itself}\:\mathrm{but}\:\mathrm{if}\:\mathrm{you}\:\mathrm{allow} \\ $$$$``\mathrm{split}\:\mathrm{points}''\:\mathrm{in}\:\mathrm{2}\:\mathrm{dimensions},\:\mathrm{how}\:\mathrm{could} \\ $$$$\mathrm{they}\:\mathrm{all}\:\mathrm{form}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com