Question Number 167301 by mnjuly1970 last updated on 12/Mar/22
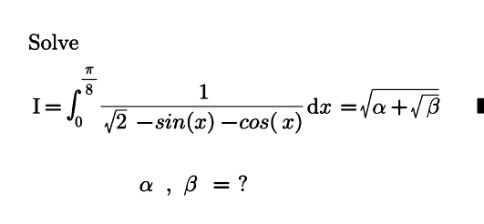
Answered by amin96 last updated on 12/Mar/22
![I=∫_0 ^(π/8) (1/( (√2)(1−cos((π/4)−x))))dx (π/4)−x=t t[(π/8); (π/4)] I=(1/( (√2)))∫_(π/8) ^(π/4) (dt/((1−cos(t))))=(1/(2(√2)))∫_(π/8) ^(π/4) csc^2 ((t/2))dt= =−(1/( (√2)))[cot((t/2))]_(π/8) ^(π/4) =−(1/( (√2)))[((sin((π/(16))−(π/8)))/(sin((π/8))sin((π/(16)))))]= =(1/( (√2)))[(1/(sin((π/8))))]=((√2)/(2(√((1−cos((π/4))/2))))=(1/( (√(1−((√2)/2)))))= =((√2)/( (√(2−(√2)))))=(((√2)×(√(2+(√2))))/( (√2)))=(√(2+(√2))) by M.A](Q167311.png)
$$\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}−\boldsymbol{\mathrm{cos}}\left(\frac{\pi}{\mathrm{4}}−\boldsymbol{\mathrm{x}}\right)\right)}\boldsymbol{\mathrm{dx}}\:\:\:\:\frac{\pi}{\mathrm{4}}−\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{t}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{t}}\left[\frac{\pi}{\mathrm{8}};\:\frac{\pi}{\mathrm{4}}\right]\:\:\:\:\boldsymbol{{I}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\frac{\pi}{\mathrm{8}}} ^{\frac{\pi}{\mathrm{4}}} \frac{\boldsymbol{\mathrm{dt}}}{\left(\mathrm{1}−\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)\right)}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\frac{\pi}{\mathrm{8}}} ^{\frac{\pi}{\mathrm{4}}} \boldsymbol{\mathrm{csc}}^{\mathrm{2}} \left(\frac{\boldsymbol{\mathrm{t}}}{\mathrm{2}}\right)\boldsymbol{\mathrm{dt}}= \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\boldsymbol{\mathrm{cot}}\left(\frac{\boldsymbol{\mathrm{t}}}{\mathrm{2}}\right)\right]_{\frac{\pi}{\mathrm{8}}} ^{\frac{\pi}{\mathrm{4}}} =−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\frac{\boldsymbol{\mathrm{sin}}\left(\frac{\pi}{\mathrm{16}}−\frac{\pi}{\mathrm{8}}\right)}{\boldsymbol{\mathrm{sin}}\left(\frac{\pi}{\mathrm{8}}\right)\boldsymbol{\mathrm{sin}}\left(\frac{\pi}{\mathrm{16}}\right)}\right]= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\frac{\mathrm{1}}{\boldsymbol{\mathrm{sin}}\left(\frac{\pi}{\mathrm{8}}\right)}\right]=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\frac{\mathrm{1}−\boldsymbol{\mathrm{cos}}\left(\frac{\pi}{\mathrm{4}}\right.}{\mathrm{2}}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}=\frac{\sqrt{\mathrm{2}}×\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:\:\:\:\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{M}}.\boldsymbol{\mathrm{A}} \\ $$
Commented by mnjuly1970 last updated on 12/Mar/22
$${thanks}\:{alot}\:{sir} \\ $$
Answered by MJS_new last updated on 12/Mar/22
$$\alpha=\beta=\mathrm{2} \\ $$
Answered by Mathspace last updated on 13/Mar/22
![changement tan((x/2))=t give I=∫_0 ^(tan((π/(16)))) ((2dt)/((1+t^2 )((√2)−((2t)/(1+t^2 ))−((1−t^2 )/(1+t^2 ))))) =2∫_0 ^(tan((π/(16)))) (dt/( (√2)(1+t^2 )−2t−1+t^2 )) =2∫_0 ^(tan((π/(16)))) (dt/( (√2)+(1+(√2))t^2 −2t−1)) =2∫_0 ^(tan((π/(16)))) (dt/((1+(√2))t^2 −2t+(√2)−1)) roots! Δ^′ =1−((√2)+1)((√2)−1) =1−(2−1)=1−1=0 one root x_0 =(1/(1+(√2)))=(√2)−1 ⇒ (1+(√2))t^2 −2t+(√2)−1=(1+(√2))(t−(√2)+1)^2 ⇒I=2∫_0 ^(tan((π/(16)))) (dt/((1+(√2))(t−(√2)+1)^2 )) =2((√2)−1)∫_0 ^(tan((π/(16)))) (dt/((t−(√2)+1)^2 )) =−2((√2)−1)[(1/(t−(√2)+1))]_0 ^(tan((π/(16)))) =2(1−(√2)){(1/(tan((π/(16)))−(√2)+1))−(1/(1+(√2)))} rest to calculate tan((π/(16))) by the formulae tan(2x)=((2tanx)/(1−tan^2 x)) ⇒ tan((π/8))=(√2)−1=((2x)/(1−x^2 )) x=tan((π/(16)))....](Q167316.png)
$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}=\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\sqrt{\mathrm{2}}−\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \:\:\frac{{dt}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−\mathrm{2}{t}−\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \:\frac{{dt}}{\:\sqrt{\mathrm{2}}+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \:\frac{{dt}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}^{\mathrm{2}} −\mathrm{2}{t}+\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$${roots}! \\ $$$$\Delta^{'} =\mathrm{1}−\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$=\mathrm{1}−\left(\mathrm{2}−\mathrm{1}\right)=\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$${one}\:{root}\:\:{x}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}}−\mathrm{1}\:\Rightarrow \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}^{\mathrm{2}} −\mathrm{2}{t}+\sqrt{\mathrm{2}}−\mathrm{1}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({t}−\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{I}=\mathrm{2}\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \:\frac{{dt}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({t}−\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\int_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \:\frac{{dt}}{\left({t}−\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left[\frac{\mathrm{1}}{{t}−\sqrt{\mathrm{2}}+\mathrm{1}}\right]_{\mathrm{0}} ^{{tan}\left(\frac{\pi}{\mathrm{16}}\right)} \\ $$$$=\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)\left\{\frac{\mathrm{1}}{{tan}\left(\frac{\pi}{\mathrm{16}}\right)−\sqrt{\mathrm{2}}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right\} \\ $$$${rest}\:{to}\:{calculate}\:{tan}\left(\frac{\pi}{\mathrm{16}}\right)\:{by}\:{the}\:{formulae} \\ $$$${tan}\left(\mathrm{2}{x}\right)=\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$${tan}\left(\frac{\pi}{\mathrm{8}}\right)=\sqrt{\mathrm{2}}−\mathrm{1}=\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${x}={tan}\left(\frac{\pi}{\mathrm{16}}\right).... \\ $$