
Question and Answers Forum
Question Number 167305 by greogoury55 last updated on 12/Mar/22
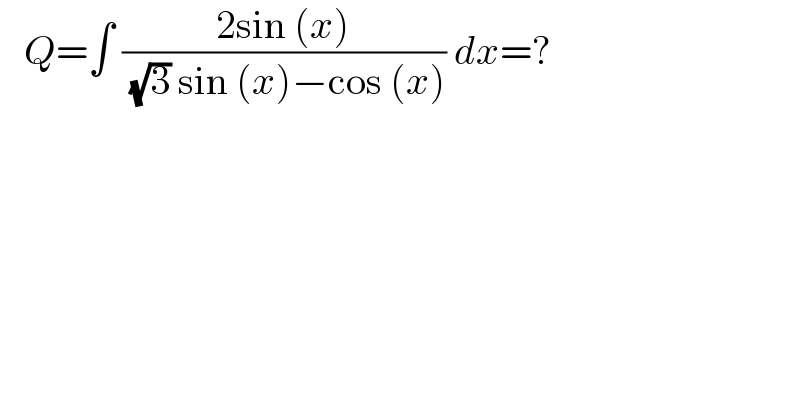
Answered by amin96 last updated on 13/Mar/22
![Q=∫((sin(x))/(((√3)/2)sin(x)−(1/2)cos(x)))dx= =−∫((sin(x))/(sin((π/6)−x)))dx (π/6)−x =t x=(π/6)−t Q=∫((sin((π/6)−t))/(sin(t)))dt= =−∫((sin(t−(π/6)))/(sin(t)))=−(1/2)∫(((√3)sin(t)−cos(t))/(sin(t)))dt= =−(1/2)(∫(√3)tdt−∫ctg(t)dt)= =−(1/2)[t(√3)−ln(sin(sin(t))]_(t=(π/6)−x) +c= =−(1/2)(((π(√3))/6)−x(√3)−ln(sin((π/6)−x))+c= =−((π(√3))/(12))+((x(√3))/2)+((ln(sin((π/6)−x)))/2)+c= =(1/2)(x(√3)+ln(sin((π/6)−x))+c](Q167327.png)
| ||
Question and Answers Forum | ||
Question Number 167305 by greogoury55 last updated on 12/Mar/22 | ||
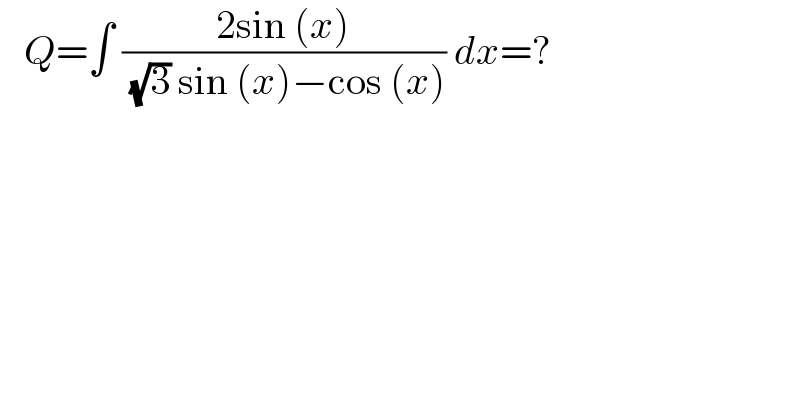 | ||
Answered by amin96 last updated on 13/Mar/22 | ||
![Q=∫((sin(x))/(((√3)/2)sin(x)−(1/2)cos(x)))dx= =−∫((sin(x))/(sin((π/6)−x)))dx (π/6)−x =t x=(π/6)−t Q=∫((sin((π/6)−t))/(sin(t)))dt= =−∫((sin(t−(π/6)))/(sin(t)))=−(1/2)∫(((√3)sin(t)−cos(t))/(sin(t)))dt= =−(1/2)(∫(√3)tdt−∫ctg(t)dt)= =−(1/2)[t(√3)−ln(sin(sin(t))]_(t=(π/6)−x) +c= =−(1/2)(((π(√3))/6)−x(√3)−ln(sin((π/6)−x))+c= =−((π(√3))/(12))+((x(√3))/2)+((ln(sin((π/6)−x)))/2)+c= =(1/2)(x(√3)+ln(sin((π/6)−x))+c](Q167327.png) | ||
| ||