
Question and Answers Forum
Question Number 167330 by LEKOUMA last updated on 13/Mar/22
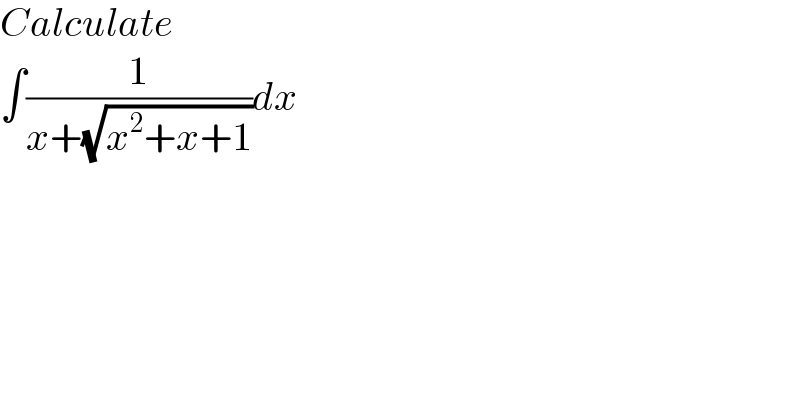
Answered by greogoury55 last updated on 13/Mar/22
![=∫ (((√(x^2 +x+1))−x)/(x+1)) dx =∫ (((√((x+(1/2))^2 +(3/4)))−x)/(x+1)) dx K_1 = ∫ ((√((x+(1/2))^2 +(3/4)))/(x+1)) dx [ x+(1/2)=((√3)/2) tan t ] K_1 =∫ ((((√3)/2) sec t )/((1/2)(1+(√3) tan t))) ((√3)/2).sec^2 t dt K_1 = (3/2)∫ ((sec^2 t)/(cos t+(√3) sin t)) dt K_1 =(3/2) ∫ ((sec^2 t)/(2((1/2)cos t+((√3)/2) sin t))) dt K_1 =(3/4)∫ ((sec^2 t)/(cos (t−(π/3)))) dt K_2 =∫ (x/(x+1))dx=∫ (((x+1)−1)/(x+1)) dx K_2 =x−ln ∣x+1∣ +c](Q167340.png)
Commented by peter frank last updated on 14/Mar/22

Answered by MJS_new last updated on 13/Mar/22
![∫(dx/(x+(√(x^2 +x+1))))=−∫((x−(√(x^2 +x+1)))/(x+1))dx= [t=x+(1/2) → dx=dt] =−∫((2t−1−(√(4t^2 +3)))/(2t+1))dt= [u=((√3)/3)(2t+(√(4t^2 +3))) → dt=(((√3)(u^2 +1))/(4u^2 ))] =((√3)/2)∫((u^2 +1)/(u^2 ((√3)u−1)))du= =∫(((2(√3))/( (√3)u−1))−(3/(2u))−((√3)/(2u^2 )))du= =2ln ((√3)u−1) −(3/2)ln u +((√3)/(2u))= ... =2ln (x+(√(x^2 +x+1))) −(3/2)ln (2x+1+(√(x^2 +x+1))) −x+(√(x^2 +x+1))+C](Q167342.png)
| ||
Question and Answers Forum | ||
Question Number 167330 by LEKOUMA last updated on 13/Mar/22 | ||
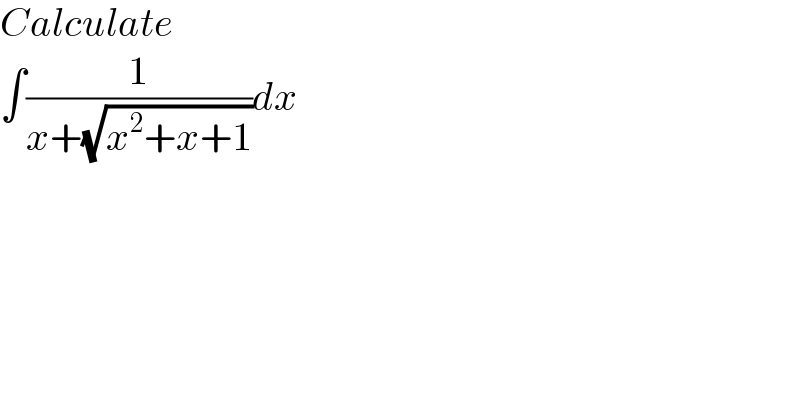 | ||
Answered by greogoury55 last updated on 13/Mar/22 | ||
![=∫ (((√(x^2 +x+1))−x)/(x+1)) dx =∫ (((√((x+(1/2))^2 +(3/4)))−x)/(x+1)) dx K_1 = ∫ ((√((x+(1/2))^2 +(3/4)))/(x+1)) dx [ x+(1/2)=((√3)/2) tan t ] K_1 =∫ ((((√3)/2) sec t )/((1/2)(1+(√3) tan t))) ((√3)/2).sec^2 t dt K_1 = (3/2)∫ ((sec^2 t)/(cos t+(√3) sin t)) dt K_1 =(3/2) ∫ ((sec^2 t)/(2((1/2)cos t+((√3)/2) sin t))) dt K_1 =(3/4)∫ ((sec^2 t)/(cos (t−(π/3)))) dt K_2 =∫ (x/(x+1))dx=∫ (((x+1)−1)/(x+1)) dx K_2 =x−ln ∣x+1∣ +c](Q167340.png) | ||
| ||
Commented by peter frank last updated on 14/Mar/22 | ||
 | ||
Answered by MJS_new last updated on 13/Mar/22 | ||
![∫(dx/(x+(√(x^2 +x+1))))=−∫((x−(√(x^2 +x+1)))/(x+1))dx= [t=x+(1/2) → dx=dt] =−∫((2t−1−(√(4t^2 +3)))/(2t+1))dt= [u=((√3)/3)(2t+(√(4t^2 +3))) → dt=(((√3)(u^2 +1))/(4u^2 ))] =((√3)/2)∫((u^2 +1)/(u^2 ((√3)u−1)))du= =∫(((2(√3))/( (√3)u−1))−(3/(2u))−((√3)/(2u^2 )))du= =2ln ((√3)u−1) −(3/2)ln u +((√3)/(2u))= ... =2ln (x+(√(x^2 +x+1))) −(3/2)ln (2x+1+(√(x^2 +x+1))) −x+(√(x^2 +x+1))+C](Q167342.png) | ||
| ||