Question Number 167644 by MJS_new last updated on 22/Mar/22
$$\mathrm{find}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{of} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}+\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}} \\ $$
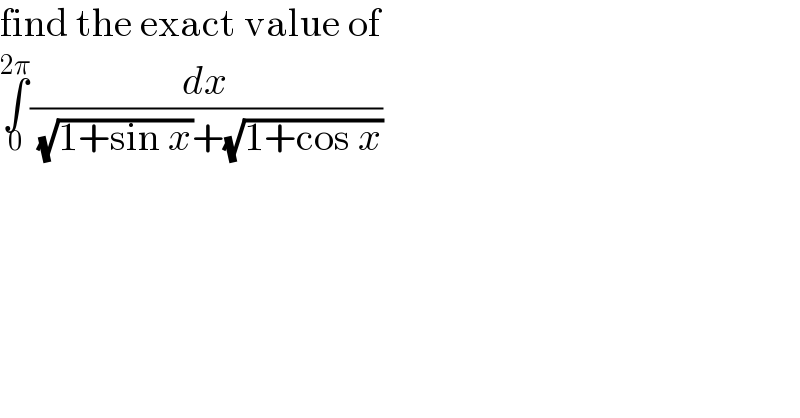
Commented by cortano1 last updated on 23/Mar/22
$${i}\:{got}\mathrm{3}.\mathrm{962}\: \\ $$$${it}\:{true}? \\ $$
Commented by MJS_new last updated on 23/Mar/22
$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{can}\:\mathrm{you}\:\mathrm{give}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}? \\ $$
Answered by greogoury55 last updated on 23/Mar/22
![∫_0 ^( 2π) (dx/( (√(1+sin x)) +(√(1+cos x)))) = 2∫_0 ^( π) (dx/(∣sin (x/2)+cos (x/2)∣+(√2) ∣cos (x/2)∣)) = 2∫_0 ^( π) (dt/(∣sin t+cos t∣+(√2) ∣cos t∣)) =∫_0 ^(π/2) ((2dt)/(sin t+(1+(√2))cos t)) + ∫_(π/2) ^((3π)/4) ((2dt)/(sin t+(1−(√2))cos t)) −∫_((3π)/4) ^π ((2dt)/(sin t+(1+(√2))cos t)) = [(4/((1+(√2))(√(4−2(√2))))) tanh^(−1) (((tan (x/4)−(√2)+1)/( (√(4−2(√2))))))]_0 ^(2π)](Q167714.png)
$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}\:+\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}\: \\ $$$$\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\pi} \frac{{dx}}{\mid\mathrm{sin}\:\frac{{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\mid+\sqrt{\mathrm{2}}\:\mid\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\mid} \\ $$$$\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\pi} \:\frac{{dt}}{\mid\mathrm{sin}\:{t}+\mathrm{cos}\:{t}\mid+\sqrt{\mathrm{2}}\:\mid\mathrm{cos}\:{t}\mid} \\ $$$$\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{dt}}{\mathrm{sin}\:{t}+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{cos}\:{t}}\:+\:\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} \frac{\mathrm{2}{dt}}{\mathrm{sin}\:{t}+\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)\mathrm{cos}\:{t}} \\ $$$$\:−\int_{\frac{\mathrm{3}\pi}{\mathrm{4}}} ^{\pi} \frac{\mathrm{2}{dt}}{\mathrm{sin}\:{t}+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{cos}\:{t}} \\ $$$$\:=\:\left[\frac{\mathrm{4}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}\:\mathrm{tanh}\:^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\frac{{x}}{\mathrm{4}}−\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$
Commented by MJS_new last updated on 23/Mar/22
$$\mathrm{I}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{I}\:\mathrm{solved}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{at} \\ $$$$\mathrm{question}\:\mathrm{167586}.\:\mathrm{but}\:\mathrm{for}\:\mathrm{the}\:\mathrm{area}\:\mathrm{we}\:\mathrm{are}\:\mathrm{not} \\ $$$$\mathrm{allowed}\:\mathrm{to}\:\mathrm{ignore}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{values} \\ $$
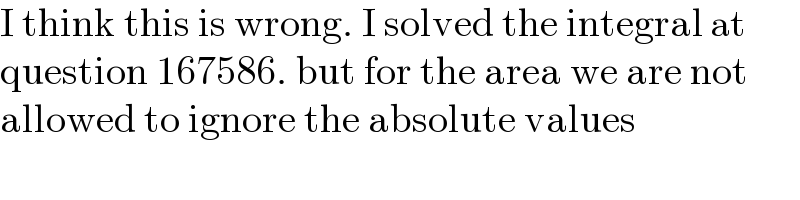
Commented by MJS_new last updated on 24/Mar/22
$${F}\left({x}\right)=\frac{\mathrm{4}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}\:\mathrm{tanh}\:^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\frac{{x}}{\mathrm{4}}−\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}}\right) \\ $$$${F}\left({x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for} \\ $$$${x}\geqslant\mathrm{4arctan}\:\left(−\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\right)\:\approx\mathrm{3}.\mathrm{927}<\mathrm{2}\pi \\ $$
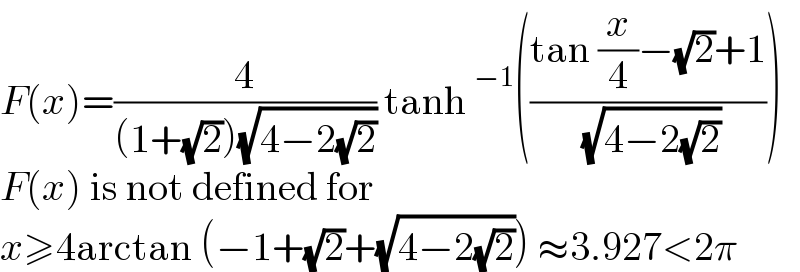
Commented by greogoury55 last updated on 24/Mar/22
$${no}\:{sir}.\:{it}\:{my}\:{answer}\:{correct}\:{but}\:{different} \\ $$$${way}\:{with}\:{your}\:{solution} \\ $$