
Question Number 167898 by peter frank last updated on 28/Mar/22

Answered by som(math1967) last updated on 29/Mar/22
![y=mx x^2 +y^2 −2ax=0 or x^2 +m^2 x^2 −2ax=0 [ ∵y=mx] or x(x+m^2 x−2a)=0 ∴ x=0, x=((2a)/(m^2 +1)) ⇒y=0 , y=((2am)/(m^2 +1)) ∴ end points of the chord (0,0) (((2a)/(m^2 +1)) ,((2am)/(m^2 +1))) mid point of the chord ((a/(m^2 +1)) , ((am)/(m^2 +1))) i.e centre of the circle which this chord is diameter (1/2)length of chord =radd of the circle =(√((a^2 /((m^2 +1)^2 ))+((a^2 m^2 )/((m^2 +1)^2 )))) =(a/( (√(m^2 +1)))) equation of the circle (x−(a/(m^2 +1)))^2 +(y−((am)/(m^2 +1)))^2 =(a^2 /(m^2 +1)) or x^2 +y^2 −((2ax)/(m^2 +1))−((2ay)/(m^2 +1)) +((a^2 (1+m^2 ))/((1+m^2 )^2 )) =(a^2 /(m^2 +1)) or (1+m^2 )(x^2 +y^2 )−2a(x+my)+a^2 =a^2 (1+m^2 )(x^2 +y^2 ) −2a(x+my)=0 [proved]](Q167903.png)
$$\:{y}={mx}\:\: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{ax}=\mathrm{0} \\ $$$${or}\:\:{x}^{\mathrm{2}} +{m}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{ax}=\mathrm{0}\:\:\left[\:\because{y}={mx}\right] \\ $$$${or}\:{x}\left({x}+{m}^{\mathrm{2}} {x}−\mathrm{2}{a}\right)=\mathrm{0} \\ $$$$\therefore\:{x}=\mathrm{0},\:\:{x}=\frac{\mathrm{2}{a}}{{m}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{y}=\mathrm{0}\:,\:{y}=\frac{\mathrm{2}{am}}{{m}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\therefore\:{end}\:{points}\:{of}\:{the}\:{chord} \\ $$$$\:\:\left(\mathrm{0},\mathrm{0}\right)\:\left(\frac{\mathrm{2}{a}}{{m}^{\mathrm{2}} +\mathrm{1}}\:,\frac{\mathrm{2}{am}}{{m}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${mid}\:{point}\:{of}\:{the}\:{chord}\: \\ $$$$\left(\frac{{a}}{{m}^{\mathrm{2}} +\mathrm{1}}\:,\:\frac{{am}}{{m}^{\mathrm{2}} +\mathrm{1}}\right)\:{i}.{e}\:{centre}\:{of}\:{the}\:{circle} \\ $$$${which}\:{this}\:{chord}\:{is}\:{diameter} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}{length}\:{of}\:{chord}\:={radd}\:{of}\:{the}\:{circle} \\ $$$$\:=\sqrt{\frac{{a}^{\mathrm{2}} }{\left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} {m}^{\mathrm{2}} }{\left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$=\frac{{a}}{\:\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${equation}\:{of}\:{the}\:{circle} \\ $$$$\left({x}−\frac{{a}}{{m}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} +\left({y}−\frac{{am}}{{m}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{{m}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:{or}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\:−\frac{\mathrm{2}{ax}}{{m}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{2}{ay}}{{m}^{\mathrm{2}} +\mathrm{1}}\:+\frac{{a}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\frac{{a}^{\mathrm{2}} }{{m}^{\mathrm{2}} +\mathrm{1}} \\ $$$${or}\:\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{a}\left({x}+{my}\right)+{a}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:−\mathrm{2}{a}\left({x}+{my}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{proved}\right] \\ $$
Commented by peter frank last updated on 29/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mr W last updated on 29/Mar/22
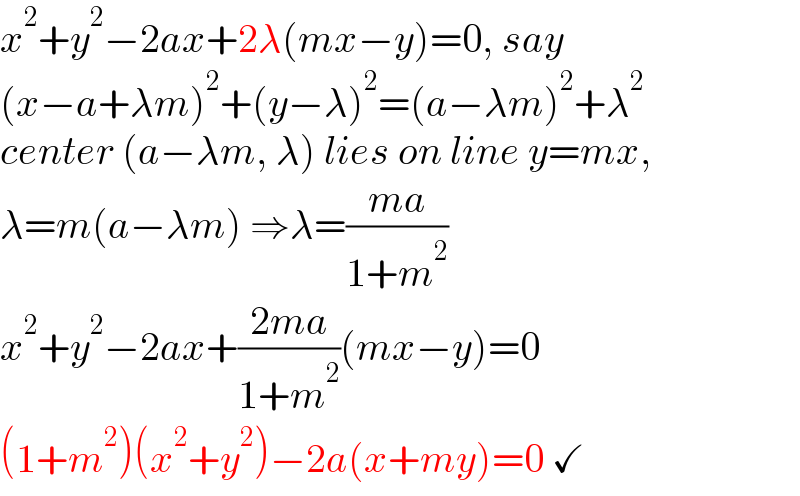
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{ax}+\mathrm{2}\lambda\left({mx}−{y}\right)=\mathrm{0},\:{say} \\ $$$$\left({x}−{a}+\lambda{m}\right)^{\mathrm{2}} +\left({y}−\lambda\right)^{\mathrm{2}} =\left({a}−\lambda{m}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} \\ $$$${center}\:\left({a}−\lambda{m},\:\lambda\right)\:{lies}\:{on}\:{line}\:{y}={mx}, \\ $$$$\lambda={m}\left({a}−\lambda{m}\right)\:\Rightarrow\lambda=\frac{{ma}}{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{ax}+\frac{\mathrm{2}{ma}}{\mathrm{1}+{m}^{\mathrm{2}} }\left({mx}−{y}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{a}\left({x}+{my}\right)=\mathrm{0}\:\checkmark \\ $$
Commented by peter frank last updated on 29/Mar/22

$$\mathrm{more}\:\mathrm{explanation}.\mathrm{First}\:\mathrm{line} \\ $$
Commented by mr W last updated on 29/Mar/22
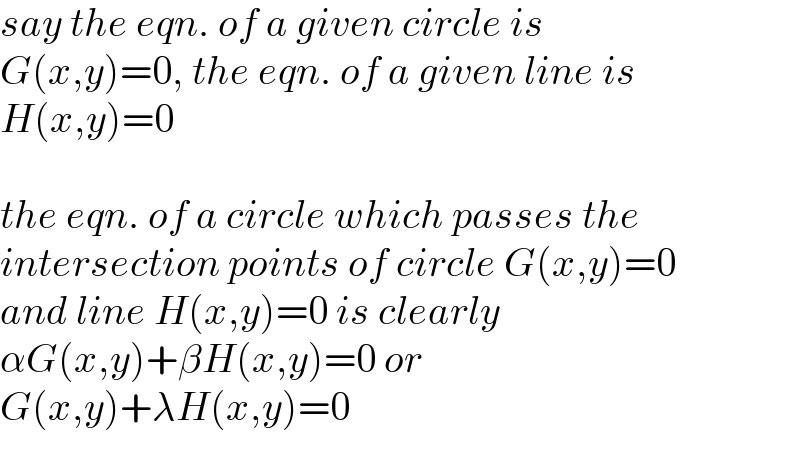
$${say}\:{the}\:{eqn}.\:{of}\:{a}\:{given}\:{circle}\:{is}\: \\ $$$${G}\left({x},{y}\right)=\mathrm{0},\:{the}\:{eqn}.\:{of}\:{a}\:{given}\:{line}\:{is} \\ $$$${H}\left({x},{y}\right)=\mathrm{0} \\ $$$$ \\ $$$${the}\:{eqn}.\:{of}\:{a}\:{circle}\:{which}\:{passes}\:{the} \\ $$$${intersection}\:{points}\:{of}\:{circle}\:{G}\left({x},{y}\right)=\mathrm{0} \\ $$$${and}\:{line}\:{H}\left({x},{y}\right)=\mathrm{0}\:{is}\:{clearly} \\ $$$$\alpha{G}\left({x},{y}\right)+\beta{H}\left({x},{y}\right)=\mathrm{0}\:{or} \\ $$$${G}\left({x},{y}\right)+\lambda{H}\left({x},{y}\right)=\mathrm{0}\: \\ $$
Commented by peter frank last updated on 29/Mar/22

$$\mathrm{thanks} \\ $$
