
Question and Answers Forum
Question Number 16794 by tawa tawa last updated on 26/Jun/17
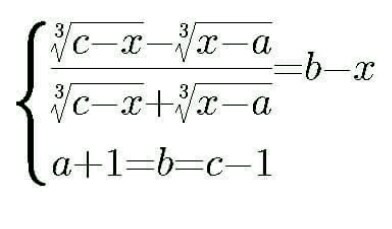
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/Jun/17
![c−x=t^3 ,x−a=s^3 ⇒x=((s^3 −t^3 )/2)+((a+c)/2) a+c=c−2+c=2(c−1)=2b,c−a=2 ((c−x))^(1/3) −((a−x))^(1/3) =(c−x−x+a)((((c−x)^2 ))^(1/3) +(((c−x)(x−a)))^(1/3) +(((a−x)^2 ))^(1/3) ) ⇒(((t−s)(t^2 −ts+s^2 ))/(c+a))=b−x ⇒t^3 −t^2 s+ts^2 −st^2 +ts^2 −s^3 =(a+c)(b−x) t^3 −s^3 −2st^2 +2ts^2 =2(b)(((t^3 −s^3 )/2)) t^3 −s^3 −2st^2 +2ts^2 =b(t^3 −s^3 ) ⇒(1−b)(t^3 −s^3 )−2ts(t−s)=0 ⇒(t−s)[(1−b)(t^2 +ts+s^2 )−2ts)=0 ⇒1)t−s=0⇒t=s⇒c−x=x−a⇒x=((c+a)/2)=b 2)t=s⇒b−x=0⇒x=b 3) (1−b)t^2 −(1+b)s.t+(1−b)s^2 =0 t=(((1+b)s±(√((1+b)^2 s^2 −4(1−b)^2 s^2 )))/(2(1−b)))= =(((1+b)s±s(√((1+b−2+2b)(1+b+2−2b))))/(2(1−b)))= =(((1+b)s±s(√((3b−1)(3−b))))/(2(1−b)))=(m±n).s [n=((√((3b−1)(3−b)))/(2(1−b))),m=((1+b)/(2(1−b)))] ⇒(t/s)=m±n⇒(t^3 /s^3 )=(m±n)^3 ⇒((c−x)/(x−a))=(m±n)^3 ⇒((2x−(a+c))/(c−a))=((1−(m±n)^3 )/(1+(m±n)^3 )) ⇒x=b+((1−(m±n)^3 )/(1+(m±n)^3 )) x=b+((1−(((1+b±(√((3b−1)(3−b))))/(2(1−b))))^3 )/(1+(((1+b±(√((3b−1)(3−b))))/(2(1−b))))^3 )) .](Q16831.png)
Commented by tawa tawa last updated on 26/Jun/17
| ||
Question and Answers Forum | ||
Question Number 16794 by tawa tawa last updated on 26/Jun/17 | ||
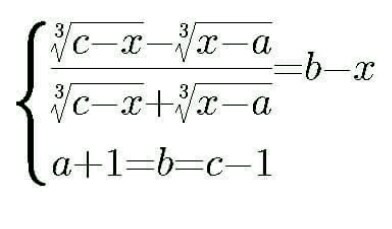 | ||
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/Jun/17 | ||
![c−x=t^3 ,x−a=s^3 ⇒x=((s^3 −t^3 )/2)+((a+c)/2) a+c=c−2+c=2(c−1)=2b,c−a=2 ((c−x))^(1/3) −((a−x))^(1/3) =(c−x−x+a)((((c−x)^2 ))^(1/3) +(((c−x)(x−a)))^(1/3) +(((a−x)^2 ))^(1/3) ) ⇒(((t−s)(t^2 −ts+s^2 ))/(c+a))=b−x ⇒t^3 −t^2 s+ts^2 −st^2 +ts^2 −s^3 =(a+c)(b−x) t^3 −s^3 −2st^2 +2ts^2 =2(b)(((t^3 −s^3 )/2)) t^3 −s^3 −2st^2 +2ts^2 =b(t^3 −s^3 ) ⇒(1−b)(t^3 −s^3 )−2ts(t−s)=0 ⇒(t−s)[(1−b)(t^2 +ts+s^2 )−2ts)=0 ⇒1)t−s=0⇒t=s⇒c−x=x−a⇒x=((c+a)/2)=b 2)t=s⇒b−x=0⇒x=b 3) (1−b)t^2 −(1+b)s.t+(1−b)s^2 =0 t=(((1+b)s±(√((1+b)^2 s^2 −4(1−b)^2 s^2 )))/(2(1−b)))= =(((1+b)s±s(√((1+b−2+2b)(1+b+2−2b))))/(2(1−b)))= =(((1+b)s±s(√((3b−1)(3−b))))/(2(1−b)))=(m±n).s [n=((√((3b−1)(3−b)))/(2(1−b))),m=((1+b)/(2(1−b)))] ⇒(t/s)=m±n⇒(t^3 /s^3 )=(m±n)^3 ⇒((c−x)/(x−a))=(m±n)^3 ⇒((2x−(a+c))/(c−a))=((1−(m±n)^3 )/(1+(m±n)^3 )) ⇒x=b+((1−(m±n)^3 )/(1+(m±n)^3 )) x=b+((1−(((1+b±(√((3b−1)(3−b))))/(2(1−b))))^3 )/(1+(((1+b±(√((3b−1)(3−b))))/(2(1−b))))^3 )) .](Q16831.png) | ||
| ||
Commented by tawa tawa last updated on 26/Jun/17 | ||
 | ||