
Question and Answers Forum
Question Number 167965 by mnjuly1970 last updated on 30/Mar/22
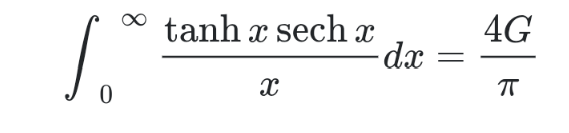
Answered by mindispower last updated on 01/Apr/22
![Ω=∫_0 ^∞ 2((1−e^(−2x) )/((1+e^(−2x) )^2 x))e^(−x) =−2∫_0 ^1 ((1−t^2 )/((1+t^2 )^2 ln(t))) =−2∫_∞ ^1 ((1−(1/t^2 ))/((1+(1/t^2 ))^2 ln((1/t)))).−(dt/t^2 ) =−2∫_1 ^∞ ((1−t^2 )/((t^2 +1)^2 ln(t)))⇒2Ω=−2∫_0 ^∞ ((1−t^2 )/((1+t^2 )ln(t)))dt f(a)=−2∫_0 ^∞ ((1−t^a )/((1+t^2 )^2 ln(t))),a∈[0,2] f(0)=0,f(2)=2Ω f′(a)=2∫_0 ^∞ (t^a /((1+t^2 )^2 ))dr =2∫_0 ^(π/2) sin^a (t)cos^(2−a) (t)dt =β(((a+1)/2),((3−a)/2))=((Γ(((a+1)/2))Γ(((3−a)/2)))/(Γ(2))) =(((1−a)/2)).(π/(sin((π/2)(1+a))))=((π(1−a))/(2cos(((πa)/2)))) 2Ω=∫_0 ^2 f′(a)da (π/2)∫_0 ^1 ((1−a)/(cos(((πa)/2))))+∫_1 ^2 ((1−a)/(cos(((πa)/2)))) =(π/2)(∫_0 ^1 ((ada)/(sin(((πa)/2))))+∫_0 ^1 ((−udu)/(cos((π/2)(1+u)))) =π∫_0 ^1 ((daa)/(sin(((πa)/2))))=(4/π)∫_0 ^(π/2) (u/(sin(u)))du ∫_0 ^(π/2) (u/(sin(u)))du=∫_0 ^(π/2) ((usin(u))/((1−cos(u))(1+cos(u))))du =(1/2)[uln(((1−cosx)/(1+cos(x))))]−(1/2)∫_0 ^(π/2) ln(((1−cos(x))/(1+cos(x)))) =−∫_0 ^(π/2) ln(tg((u/2)))du=−2∫_0 ^1 ((ln(x))/(1+x^2 ))=2G ⇒2Ω=(4/π).2G Ω=∫_0 ^∞ ((tanh (x))/x).sech (x)dx=((4G)/π)](Q168038.png)
| ||
Question and Answers Forum | ||
Question Number 167965 by mnjuly1970 last updated on 30/Mar/22 | ||
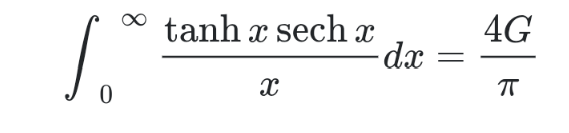 | ||
Answered by mindispower last updated on 01/Apr/22 | ||
![Ω=∫_0 ^∞ 2((1−e^(−2x) )/((1+e^(−2x) )^2 x))e^(−x) =−2∫_0 ^1 ((1−t^2 )/((1+t^2 )^2 ln(t))) =−2∫_∞ ^1 ((1−(1/t^2 ))/((1+(1/t^2 ))^2 ln((1/t)))).−(dt/t^2 ) =−2∫_1 ^∞ ((1−t^2 )/((t^2 +1)^2 ln(t)))⇒2Ω=−2∫_0 ^∞ ((1−t^2 )/((1+t^2 )ln(t)))dt f(a)=−2∫_0 ^∞ ((1−t^a )/((1+t^2 )^2 ln(t))),a∈[0,2] f(0)=0,f(2)=2Ω f′(a)=2∫_0 ^∞ (t^a /((1+t^2 )^2 ))dr =2∫_0 ^(π/2) sin^a (t)cos^(2−a) (t)dt =β(((a+1)/2),((3−a)/2))=((Γ(((a+1)/2))Γ(((3−a)/2)))/(Γ(2))) =(((1−a)/2)).(π/(sin((π/2)(1+a))))=((π(1−a))/(2cos(((πa)/2)))) 2Ω=∫_0 ^2 f′(a)da (π/2)∫_0 ^1 ((1−a)/(cos(((πa)/2))))+∫_1 ^2 ((1−a)/(cos(((πa)/2)))) =(π/2)(∫_0 ^1 ((ada)/(sin(((πa)/2))))+∫_0 ^1 ((−udu)/(cos((π/2)(1+u)))) =π∫_0 ^1 ((daa)/(sin(((πa)/2))))=(4/π)∫_0 ^(π/2) (u/(sin(u)))du ∫_0 ^(π/2) (u/(sin(u)))du=∫_0 ^(π/2) ((usin(u))/((1−cos(u))(1+cos(u))))du =(1/2)[uln(((1−cosx)/(1+cos(x))))]−(1/2)∫_0 ^(π/2) ln(((1−cos(x))/(1+cos(x)))) =−∫_0 ^(π/2) ln(tg((u/2)))du=−2∫_0 ^1 ((ln(x))/(1+x^2 ))=2G ⇒2Ω=(4/π).2G Ω=∫_0 ^∞ ((tanh (x))/x).sech (x)dx=((4G)/π)](Q168038.png) | ||
| ||