Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 168208 by MathsFan last updated on 06/Apr/22

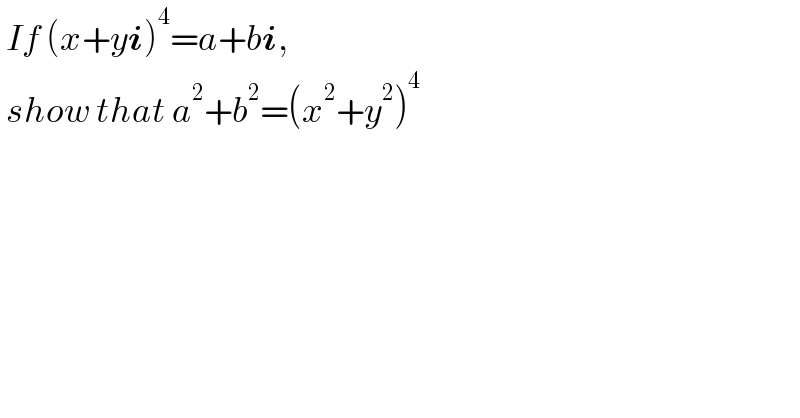
If (x+yi)^4 =a+bi, show that a^2 +b^2 =(x^2 +y^2 )^4

$$\:{If}\:\left({x}+{y}\boldsymbol{{i}}\right)^{\mathrm{4}} ={a}+{b}\boldsymbol{{i}}, \\ $$$$\:{show}\:{that}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{4}} \\ $$

Commented by MJS_new last updated on 06/Apr/22

you can do it yourself (1) expand (x+yi)^4 =term1 (2) a=real (term1) ∧ b=imag (term1) (3) expand a^2 +b^2 =term2 (4) sort term2 and you should see the factors 1 4 6 4 1 ⇒ there you are

$$\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{it}\:\mathrm{yourself} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{expand}\:\left({x}+{y}\mathrm{i}\right)^{\mathrm{4}} =\mathrm{term1} \\ $$$$\left(\mathrm{2}\right)\:{a}=\mathrm{real}\:\left(\mathrm{term1}\right)\:\wedge\:{b}=\mathrm{imag}\:\left(\mathrm{term1}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{expand}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{term2} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{sort}\:\mathrm{term2}\:\mathrm{and}\:\mathrm{you}\:\mathrm{should}\:\mathrm{see}\:\mathrm{the} \\ $$$$\:\:\:\:\:\mathrm{factors}\:\mathrm{1}\:\mathrm{4}\:\mathrm{6}\:\mathrm{4}\:\mathrm{1}\:\Rightarrow\:\mathrm{there}\:\mathrm{you}\:\mathrm{are} \\ $$

Answered by mr W last updated on 06/Apr/22

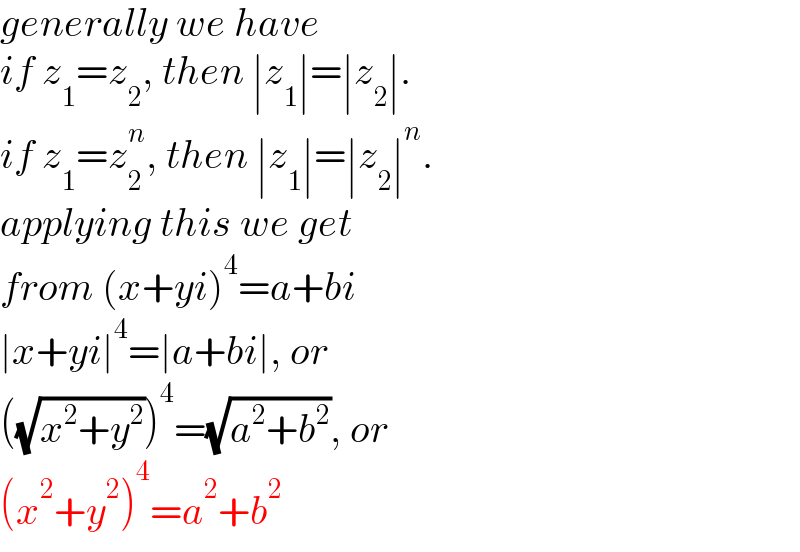
generally we have if z_1 =z_2 , then ∣z_1 ∣=∣z_2 ∣. if z_1 =z_2 ^n , then ∣z_1 ∣=∣z_2 ∣^n . applying this we get from (x+yi)^4 =a+bi ∣x+yi∣^4 =∣a+bi∣, or ((√(x^2 +y^2 )))^4 =(√(a^2 +b^2 )), or (x^2 +y^2 )^4 =a^2 +b^2

$${generally}\:{we}\:{have} \\ $$$${if}\:{z}_{\mathrm{1}} ={z}_{\mathrm{2}} ,\:{then}\:\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid. \\ $$$${if}\:{z}_{\mathrm{1}} ={z}_{\mathrm{2}} ^{{n}} ,\:{then}\:\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid^{{n}} . \\ $$$${applying}\:{this}\:{we}\:{get}\: \\ $$$${from}\:\left({x}+{yi}\right)^{\mathrm{4}} ={a}+{bi} \\ $$$$\mid{x}+{yi}\mid^{\mathrm{4}} =\mid{a}+{bi}\mid,\:{or} \\ $$$$\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)^{\mathrm{4}} =\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} },\:{or} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{4}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$

Commented by MathsFan last updated on 19/Apr/22

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by Mathspace last updated on 06/Apr/22

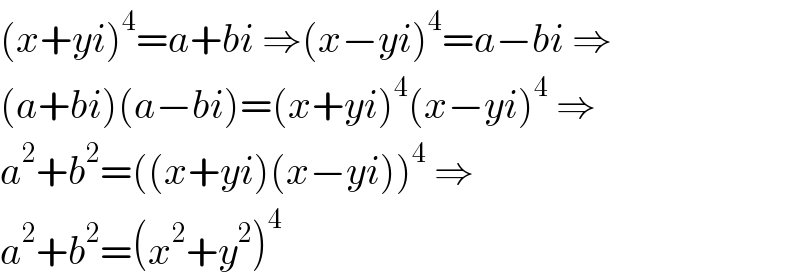
(x+yi)^4 =a+bi ⇒(x−yi)^4 =a−bi ⇒ (a+bi)(a−bi)=(x+yi)^4 (x−yi)^4 ⇒ a^2 +b^2 =((x+yi)(x−yi))^4 ⇒ a^2 +b^2 =(x^2 +y^2 )^4

$$\left({x}+{yi}\right)^{\mathrm{4}} ={a}+{bi}\:\Rightarrow\left({x}−{yi}\right)^{\mathrm{4}} ={a}−{bi}\:\Rightarrow \\ $$$$\left({a}+{bi}\right)\left({a}−{bi}\right)=\left({x}+{yi}\right)^{\mathrm{4}} \left({x}−{yi}\right)^{\mathrm{4}} \:\Rightarrow \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left(\left({x}+{yi}\right)\left({x}−{yi}\right)\right)^{\mathrm{4}} \:\Rightarrow \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{4}} \\ $$

Commented by mr W last updated on 07/Apr/22

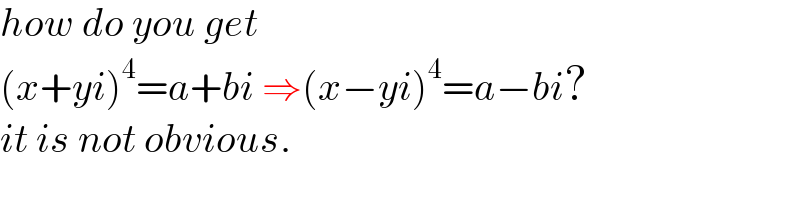
how do you get (x+yi)^4 =a+bi ⇒(x−yi)^4 =a−bi? it is not obvious.

$${how}\:{do}\:{you}\:{get} \\ $$$$\left({x}+{yi}\right)^{\mathrm{4}} ={a}+{bi}\:\Rightarrow\left({x}−{yi}\right)^{\mathrm{4}} ={a}−{bi}? \\ $$$${it}\:{is}\:{not}\:{obvious}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com