Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 168244 by mnjuly1970 last updated on 07/Apr/22

Answered by MJS_new last updated on 07/Apr/22

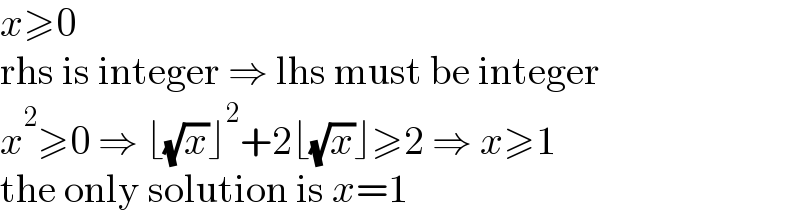
x≥0 rhs is integer ⇒ lhs must be integer x^2 ≥0 ⇒ ⌊(√x)⌋^2 +2⌊(√x)⌋≥2 ⇒ x≥1 the only solution is x=1

$${x}\geqslant\mathrm{0} \\ $$$$\mathrm{rhs}\:\mathrm{is}\:\mathrm{integer}\:\Rightarrow\:\mathrm{lhs}\:\mathrm{must}\:\mathrm{be}\:\mathrm{integer} \\ $$$${x}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow\:\lfloor\sqrt{{x}}\rfloor^{\mathrm{2}} +\mathrm{2}\lfloor\sqrt{{x}}\rfloor\geqslant\mathrm{2}\:\Rightarrow\:{x}\geqslant\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:{x}=\mathrm{1} \\ $$

Commented by mnjuly1970 last updated on 07/Apr/22

thx alot..

$$\:{thx}\:{alot}.. \\ $$

Answered by floor(10²Eta[1]) last updated on 07/Apr/22

⌊(√x)⌋=n≥0∈Z⇒(√x)=n+α, 0≤α<1 ⇒x^2 =(n+α)^4 and x^2 =n^2 +2n−2 0≤α<1⇒n^4 ≤(n+α)^4 <(n+1)^4 ⇒n^4 ≤x^2 <(n+1)^4 ⇒n^4 ≤n^2 +2n−2<(n+1)^4 let f(n)=n^4 −n^2 −2n+2, we want f(n)≤0 f(0)=2, f(1)=−1⇒n≥1 if we show that f(n) is decreasing for n≥1 we′re done f′(n)=4n^3 −2n−2≤0⇒2n^3 ≤n+1 this inequality is true for n=1, but for n≥2 it seems to be false lets show that 2n^3 ≥n+1, ∀n≥2 (induction) suppose it′s true for any k≥2 2k^3 ≥k+1, let′s show its true for k+1 2(k+1)^3 =2k^3 +6k^2 +6k+2≥6k^2 +7k+3≥7k+3≥k+2 so, in fact n=1 is the only value that makes f(n)≤0 ⇒(√x)=α+1⇒1≤(√x)<2⇒⌊(√x)⌋=1 ⇒x^2 =1⇒x=1

$$\lfloor\sqrt{\mathrm{x}}\rfloor=\mathrm{n}\geqslant\mathrm{0}\in\mathbb{Z}\Rightarrow\sqrt{\mathrm{x}}=\mathrm{n}+\alpha,\:\mathrm{0}\leqslant\alpha<\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\left(\mathrm{n}+\alpha\right)^{\mathrm{4}} \:\mathrm{and}\:\mathrm{x}^{\mathrm{2}} =\mathrm{n}^{\mathrm{2}} +\mathrm{2n}−\mathrm{2} \\ $$$$\mathrm{0}\leqslant\alpha<\mathrm{1}\Rightarrow\mathrm{n}^{\mathrm{4}} \leqslant\left(\mathrm{n}+\alpha\right)^{\mathrm{4}} <\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{n}^{\mathrm{4}} \leqslant\mathrm{x}^{\mathrm{2}} <\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} \Rightarrow\mathrm{n}^{\mathrm{4}} \leqslant\mathrm{n}^{\mathrm{2}} +\mathrm{2n}−\mathrm{2}<\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{n}\right)=\mathrm{n}^{\mathrm{4}} −\mathrm{n}^{\mathrm{2}} −\mathrm{2n}+\mathrm{2},\:\mathrm{we}\:\mathrm{want}\:\mathrm{f}\left(\mathrm{n}\right)\leqslant\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{2},\:\mathrm{f}\left(\mathrm{1}\right)=−\mathrm{1}\Rightarrow\mathrm{n}\geqslant\mathrm{1} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{show}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{n}\right)\:\mathrm{is}\:\mathrm{decreasing}\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{1}\:\mathrm{we}'\mathrm{re}\:\mathrm{done} \\ $$$$\mathrm{f}'\left(\mathrm{n}\right)=\mathrm{4n}^{\mathrm{3}} −\mathrm{2n}−\mathrm{2}\leqslant\mathrm{0}\Rightarrow\mathrm{2n}^{\mathrm{3}} \leqslant\mathrm{n}+\mathrm{1} \\ $$$$\mathrm{this}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{1},\: \\ $$$$\mathrm{but}\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{2}\:\mathrm{it}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\mathrm{false} \\ $$$$\mathrm{lets}\:\mathrm{show}\:\mathrm{that}\:\mathrm{2n}^{\mathrm{3}} \geqslant\mathrm{n}+\mathrm{1},\:\forall\mathrm{n}\geqslant\mathrm{2}\:\left(\mathrm{induction}\right) \\ $$$$\mathrm{suppose}\:\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:\mathrm{any}\:\mathrm{k}\geqslant\mathrm{2} \\ $$$$\mathrm{2k}^{\mathrm{3}} \geqslant\mathrm{k}+\mathrm{1},\:\mathrm{let}'\mathrm{s}\:\mathrm{show}\:\mathrm{its}\:\mathrm{true}\:\mathrm{for}\:\mathrm{k}+\mathrm{1} \\ $$$$\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{2k}^{\mathrm{3}} +\mathrm{6k}^{\mathrm{2}} +\mathrm{6k}+\mathrm{2}\geqslant\mathrm{6k}^{\mathrm{2}} +\mathrm{7k}+\mathrm{3}\geqslant\mathrm{7k}+\mathrm{3}\geqslant\mathrm{k}+\mathrm{2} \\ $$$$\mathrm{so},\:\mathrm{in}\:\mathrm{fact}\:\mathrm{n}=\mathrm{1}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only}\:\mathrm{value}\:\mathrm{that}\:\mathrm{makes}\:\mathrm{f}\left(\mathrm{n}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{x}}=\alpha+\mathrm{1}\Rightarrow\mathrm{1}\leqslant\sqrt{\mathrm{x}}<\mathrm{2}\Rightarrow\lfloor\sqrt{\mathrm{x}}\rfloor=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{1} \\ $$

Answered by mr W last updated on 07/Apr/22

let t=(√x) t^4 =[t]^2 +2[t]−2=integer ⇒t is also integer ⇒[t]=t t^4 =t^2 +2t−2=0 (t^2 +2t+2)(t−1)^2 =0 ⇒t=1 is the only integer solution ⇒(√x)=t=1 ⇒x=1

$${let}\:{t}=\sqrt{{x}} \\ $$$${t}^{\mathrm{4}} =\left[{t}\right]^{\mathrm{2}} +\mathrm{2}\left[{t}\right]−\mathrm{2}={integer} \\ $$$$\Rightarrow{t}\:{is}\:{also}\:{integer}\:\Rightarrow\left[{t}\right]={t} \\ $$$${t}^{\mathrm{4}} ={t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{2}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}\right)\left({t}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{1}\:{is}\:{the}\:{only}\:{integer}\:{solution} \\ $$$$\Rightarrow\sqrt{{x}}={t}=\mathrm{1}\:\Rightarrow{x}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com