
Question and Answers Forum
Question Number 168459 by BegamovSirojiddin last updated on 11/Apr/22

Answered by Mathspace last updated on 11/Apr/22
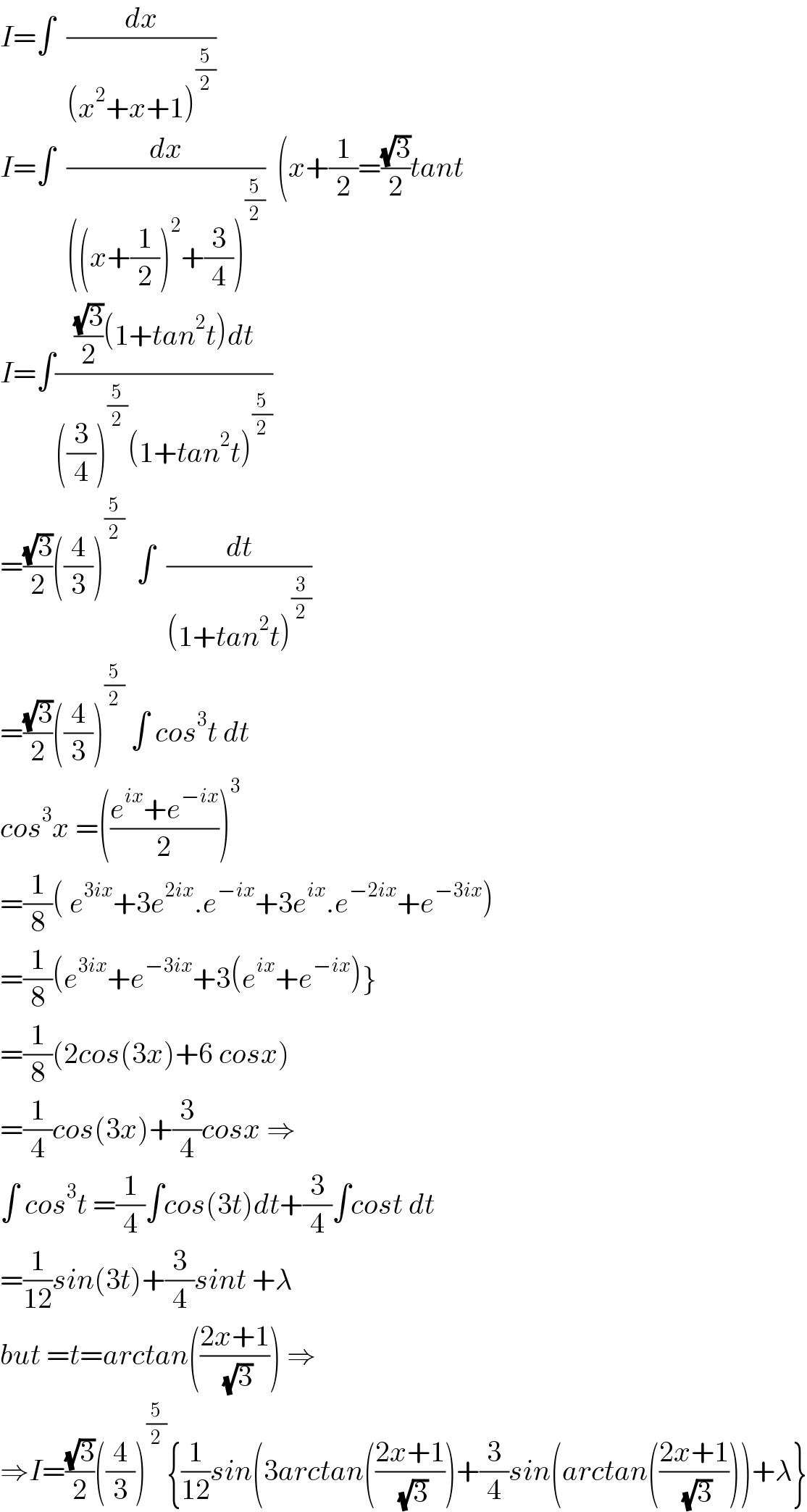
Answered by MJS_new last updated on 11/Apr/22
![∫(dx/((x^2 +x+1)^(5/2) ))= [t=((2x+1+2(√(x^2 +x+1)))/( (√3))) → dx=((√(x^2 +x+1))/t)dt] =((256)/9)∫(t^3 /((t^2 +1)^4 ))dt=((256)/9)∫((t/((t^2 +1)^3 ))−(t/((t^2 +1)^4 )))dt= =−((64)/(9(t^2 +1)^2 ))+((128)/(27(t^2 +1)^3 ))=−((64(3t^2 +1))/(27(t^2 +1)^3 ))= =((2(2x+1)(8x^2 +8x+11))/(27(x^2 +x+1)^(3/2) ))+C](Q168483.png)
| ||
Question and Answers Forum | ||
Question Number 168459 by BegamovSirojiddin last updated on 11/Apr/22 | ||
 | ||
Answered by Mathspace last updated on 11/Apr/22 | ||
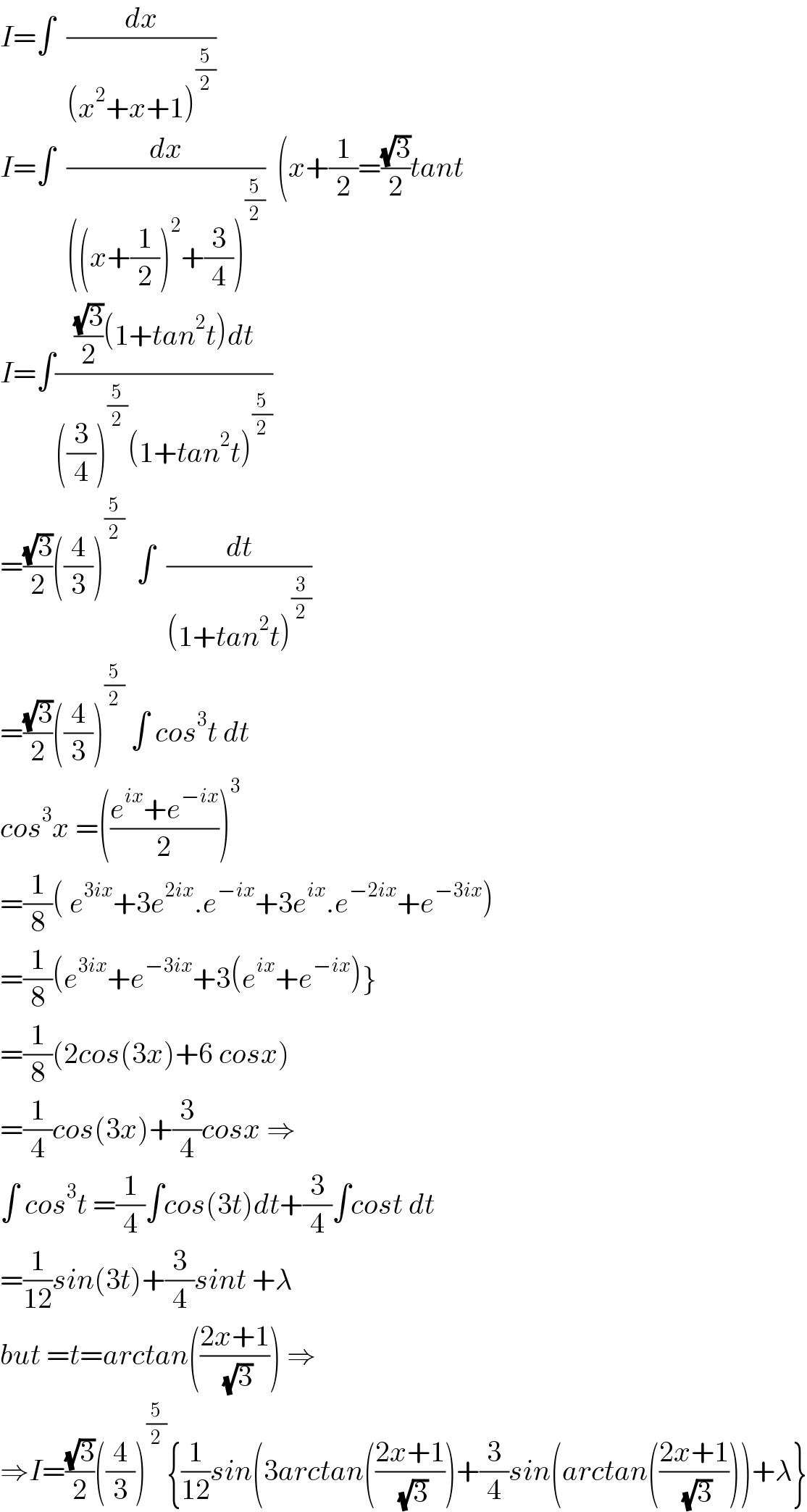 | ||
| ||
Answered by MJS_new last updated on 11/Apr/22 | ||
![∫(dx/((x^2 +x+1)^(5/2) ))= [t=((2x+1+2(√(x^2 +x+1)))/( (√3))) → dx=((√(x^2 +x+1))/t)dt] =((256)/9)∫(t^3 /((t^2 +1)^4 ))dt=((256)/9)∫((t/((t^2 +1)^3 ))−(t/((t^2 +1)^4 )))dt= =−((64)/(9(t^2 +1)^2 ))+((128)/(27(t^2 +1)^3 ))=−((64(3t^2 +1))/(27(t^2 +1)^3 ))= =((2(2x+1)(8x^2 +8x+11))/(27(x^2 +x+1)^(3/2) ))+C](Q168483.png) | ||
| ||